双馈风机惯性响应控制系统研究

／华锐风电科技（集团）股份有限公司 汪锋／

双馈风机惯性响应控制系统研究

／华锐风电科技（集团）股份有限公司 汪锋／

本文介绍了多种针对双馈风力发电机组的惯性响应控制算法。当风电场电网频率发生变化时，风力发电机组可利用其惯性调节其有功或力矩输出，实现对于电网频率的有效暂态控制，并提供短时有功功率支撑，有助于电力系统恢复和电网稳定运行。

风机惯性响应；频率特性

0 引言

近年来，随着新能源行业的高速发展，国内的风电装机无论在数量和速度上都创造了新的世界奇迹，然而，风力发电在向人类贡献着大量清洁能源的同时，也给电网运行带来了一定的困难，主要体现在以下两个方面：一方面，风资源具有一定的波动性和不确定性，如夏天的风速普遍比夏天的偏小，白天的风速普遍比晚上偏小，而正是由于这种不确定性，导致了在电力系统调节过程之中，需要使用其他的电源，如火电，水电等对其进行调峰调频，且由于当前风资源的预测技术还不够完善，导致这种调峰、调频难度较大；另一方面，随着风电并网运行渗透率的逐步增大，利用风电参与电网频率调整，增大系统稳定性已成为发展趋势和主要研究方向。同时，由于风机自身的特点，风电场代替常规电源后会导致电力系统惯量减小，当出现因电源发生故障脱网或者因负荷发生突变出现扰动等情况时，电力系统会出现更大的频率偏差和更快的频率下降速度。

双馈异步风电机组可通过实现虚拟惯量控制，来提高电力系统的频率稳定性。虚拟惯量响应控制策略主要分为两种实现方式：

1）由于双馈机组实现了有功和无功控制的解耦，当发生频率扰动时，可通过改变机组有功功率控制参考值，来实现有功功率的暂态调节；

2）在风机的最优力矩控制策略中引入频率偏差或频率的微分项，通过PID控制器环节，调节力矩参考值，从而实现有功功率的暂态调整。

本文将从有功控制策略和力矩控制策略两个方面入手展开具体研究工作，比较不同控制策略之间的优劣，为后续具体实施提供理论参考。需要说明的是，在本仿真实验中，为了方便对比分析，设定了风速保持不变的原则。

1 风机的频率响应特性

1.1 建立风电场模型

在DIgSILENT/PowerFactory软件下搭建小型电力系统模型，该风场含150台1.5MW等值双馈风机、1台50MW同步发电机、270MW的等效负荷，接着，设置同步发电机为SL节点，图1为该仿真模型对应的单线图，图2为不加负荷扰动和任何控制策略时的风场运行情况。

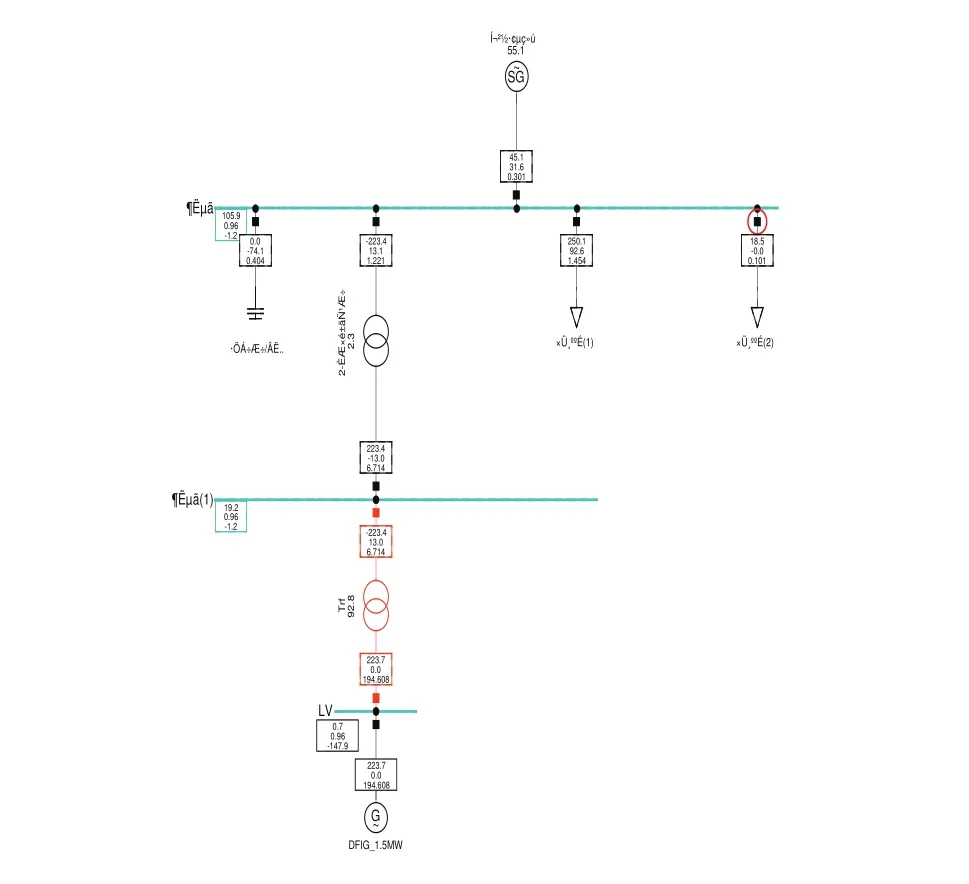
图1 系统单线图

从图2中可以看出该系统在不加任何扰动和控制策略时，系统频率保持50Hz不变，风机实际出力与转速也保持不变，系统处于稳定运行状态。

1.2 功率波动下的风机频率响应

为研究双馈风机对系统频率波动的响应情况，在上述仿真中的20s时增加20MW的负荷功率，同时，观察当负荷功率波动时，系统主要参数（如有功、转速等）的变化情况，仿真结果如图3所示。

图2 不加任何扰动和控制策略

图3 增加负荷扰动时的风机响应特征

从图3所显示的仿真结果可以看出，当系统负荷功率增加，频率发生波动时，双馈风力发电机的有功功率基本保持不变，其转速也维持恒定不变，这表明如果不添加任何频率辅助控制措施时，双馈风力发电机无法对系统频率波动做出任何响应。

2 双馈机组惯性响应控制策略研究

2.1 惯性控制原理

常规同步发电机的转速与频率存在耦合关系，当电网频率波动时，转子转速会随频率自动改变，进而转子动能改变，通过吸收或释放转子动能阻止系统频率的快速变化。而双馈风电机组采用电力电子变换器能够灵活的调节有功、无功，为了实现最大风能捕获，追踪最大功率点运行，使风机转速和电网频率之间不存在耦合关系，导致风电机组无法响应频率的变化，失去了常规发电机组所具备的惯性响应能力。

虽然双馈发电机频率与转速之间不存在耦合关系，但双馈风机发电机相比常规同步发电机而言，释放动能的潜力巨大，对系统转动惯量的影响一样存在。因此，在研究频率响应时采用了惯量控制。

惯量控制原理主要是指为了实现转子转速和电网频率变化的同步，在风机原有的控制策略基础上，通过引入频率变化率df／dt，相当于转子转速变化率dw／dt（因 f =ω／2π），进而获得惯性响应对应的力矩补偿控制值Tsc（Tsc=2Hdf／dt）或有功补偿控制值 Psc= kpdf／dt，将其附加在风电机组的力矩控制目标值或有功控制目标上，能够有效利用转子动能实现惯量响应。引入△f，也可以实现模拟惯量响应 Tsc= 2Hd 或 Psc= kpdf／dt = kp（f - fref）。

图4为风机整体控制框图。

图4 风机整体控制框图

2.2 有功功率补偿控制

在本章节中，主要是通过仿真，采用补充有功功率补偿控制实现惯量响应时，观察风机的响应特征和系统频率变化，在图4红色框中，对于风机有功-频特性所对应的基本模型中增加补充控制，图5为其控制框图。

分别开展详细的对比工作，下面分别对不加任何控制、只引入△f，只引入df／dt、引入△f和df／dt的情况进行了仿真。

图6为引入△f控制回路和不加任何控制仿真结果。

从图6的仿真结果可以看出，扰动最初的几秒内，系统频率变化较小，频率跌落最低点被抬高。这说明有惯性控制环节的DFIG机组对系统频率调节有一定的支撑作用，但是对系统频率最终稳态值并没有改变（虚拟惯量控制是通过调整转子转速释放转子部分动能增大风机输出功率，并不能调整输入的能量值，因此只能提供短暂的有功支撑，不能改变最终的稳态值。）。

图5 有功补充控制框图

图6 对比引入△f控制回路和不加任何控制

图7 对比引入df／dt控制回路和不加任何控制

图8 几种控制方式的对比结果

图7为引入df／dt回路和不加任何控制的仿真结果。

从图7可以看出，引入含df／dt回路的惯性控制后，频率跌落点相比不加控制时被抬高，但对系统频率的最终稳定值也没有影响。

图8为不加控制、只含df／dt控制回路、只含△f控制回路、含df／dt和△f控制回路的对比仿真结果。

从图8中可以看出，含△f和df／dt控制回路的惯性控制相比单一控制回路而言，会进一步提高频率跌落点，频率变化率最小。

综上，增加惯性响应控制环节后，等效增大了系统惯量，使DFIG机组能够向常规同步发电机一样对系统频率具有惯性响应能力，虽然这种具有惯性控制环节的DFIG机组对系统频率调节具有一定的支撑作用，能够减小系统频率变化率，抬高频率跌落点，但是不能改善频率最终稳态偏差，如果要改善系统的最终稳态误差，需要从风电场有功容量旋转备用上入手，采用有功功率备用或风机变桨角度备用等方式来实现，本文将不作深入研究。

2.3 力矩补偿控制

因 P=ωT，可以通过增加力矩T的方式增大功率，进而影响系统频率的大小。即在图4中蓝色框所对应的一般模型补充力矩。图9为力矩补充控制框图。

图9 力矩补充控制

分别对比了不加任何控制、只引入△f，只引入df／dt、引入△f和df／dt时的仿真结果。

图10为引入控制回路和不加任何控制仿真结果。

图10 只含△f回路的惯性控制和不加控制对比结果

从图10的仿真结果可以看出，扰动最初的几秒内，系统频率变化较小，频率跌落最低点被抬高。这说明有惯性控制环节的DFIG机组对系统频率调节有一定的支撑作用，但是对系统频率最终稳态值并没有改变。

图11为引入df／dt回路和不加任何控制的仿真结果。

图11 只含df／dt回路的惯性控制和不加控制对比结果

从图11可以看出，引入含df／dt回路的惯性控制后，频率跌落点相比不加控制时被抬高，但对系统频率的最终稳定值也没有影响。

图12为不加控制、只含df／dt控制回路、只含△f控制回路、含df／dt和△f控制回路的对比仿真结果。

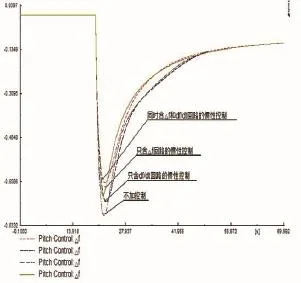
图12 几种控制方式的对比结果

图10、图11、图12的分析结果同有功补充控制的分析结果，唯一不同之处在于有功补充控制的控制目标是功率P，力矩补充控制的控制目标是T。从图12最终对比结果可以看出同时含△f和df／dt回路的惯性控制对频率最低跌落点的提升能力最强。

3 惯性控制策略比较分析

针对上述所提到的有功功率控制和力矩控制策略，为了直观清晰地看出不同算法之间的控制效果，开展了对比分析工作，图13不加控制、只含df／dt控制回路、只含△f控制回路、含df／dt和△f控制回路的对比仿真结果，其中包括风机有功功率、系统频率、力矩的变化情况。

从图13可以看出df／dt和△f两种控制方式结合相比只含△f或只含df／dt回路的控制效果都要好，两种控制方式相结合能够更快、更多地增大有功和力矩，更准确地响应负荷扰动。仿真结果显示在负荷扰动时，有功功率和力矩瞬间被提升到最大值，频率跌落点明显升高。

从风机控制系统的实现角度来看，使用基于力矩控制的惯性控制策略难度较小，在原有的基于转速的最优力矩控制的基础之上增加惯性力矩部分，从而将最终的力矩给定值交给变频器执行，控制效果高，稳定好。

4 结束语

随着国家新能源战略的进一步推进和实施，风电的装机将进一步增加，风电的渗漏率还将进一步提升，因此，开展风力发电机组参与暂态调频的研究具有重要的价值和意义，由于现有的大部分风力发电机组不具备频率响应能力，因此通过修改风机的控制策略，增加风机的针对电网频率的响应能力，可以有效地抑制电网的频率波动，维持电力系统稳定和电网安全。