数学娱乐(十八)
——高等数学的3个问题
耿 济
(海南大学,海南 海口 570228)
数学娱乐(十八)
——高等数学的3个问题
耿 济
(海南大学,海南 海口 570228)
本文分为3部分,第1部分是等价莱布尼兹定理,第2部分是对应欧拉公式,第3部分是三角函数推广.
等价莱布尼兹定理; 对应欧拉公式; 三角函数推广
本文是数学娱乐系列文献[1-17]的续作.
学习高等数学要有兴趣、要有发现问题和解决问题的能力,才能有所收获.笔者首先从莱布尼兹定理、欧拉公式以及三角函数展开式上发现有关3个问题,其依次解决有关3个问题获得等价莱布尼兹定理、对应欧拉公式以及三角函数推广.
1 等价莱布尼兹定理
首先,简介莱布尼兹定理以及发现过程.
据说莱布尼兹观察一批导数公式
(fg)′=f′g+fg′,
(fg)″=f″g+2f′g′+fg″,
(fg)‴=f‴g+3f″g′+3f′g″+fg‴,
… … …
从特殊到一般的导数公式,经过证明得到结果.
莱布尼兹定理 设n为正整数,函数f(x),g(x)在区间I上n阶可导,就有
其次,把前面的一批导数公式改成一批新的公式
f′g+fg′=(fg)′,
f″g+fg″=(fg)″-2f′g′,
f‴g+fg‴=(fg)‴-3(f′g′)′,
f″″g+fg″″=(fg)″″-4(f′g′)″+2f″g″,
… … …
假设函数f(x)=eax,g(x)=ebx代入,左右两式约去函数e(a+b)x≠0后,出现代数恒等式
a+b=(a+b),
a2+b2=(a+b)2-2ab,
a3+b3=(a+b)3-3(a+b)ab,
a4+b4=(a+b)4-4(a+b)2ab+2(ab)2,
… … …
远在1754年拉格朗日得到的结果[18]
现在获得下述结果
等价莱布尼兹定理 设n为正整数,函数f(x),g(x)在区间I上n阶可导,就有

证明 已知n=1,2时定理成立,假设2 应用简单的导数公式 f(k)g+fg(k)=(f(k-1)g+fg(k-1))′-((f′)(n-2)g′+f′(g′)n-2) , 把假设成立的结果代入后,经过整理合并得到 所以当n=k时定理成立,证毕. 其次,关于等价性的证明,应用组合与圆组合恒等式[14] 其中,0 最后,关于一般莱布尼兹定理的结果,请参考湘潭大学唐祐华教授新书的结果[18]. 推广莱布尼兹定理 设n为正整数,实数或复数a0,a1,a2,…,an,且ak=an-k,0≤k≤n,函数f(x),g(x)在区间I上n阶可导,就有 这一结果包含上述莱布尼兹定理和等价莱布尼兹定理,还包含无穷多个等价莱布尼兹定理. 首先,简介欧拉公式及其发现过程. 据说欧拉观察下述函数展开式 发现把exp(x)中的x换成ix后得出等式,经过证明成立. 欧拉公式 exp(ix)=cosx+i sinx. 图1 函数关系 通过图1说明对数函数与反三角函数之间可能存在对应欧拉公式的关系. 熟知有理函数不定积分出现对数函数和反正切函数,例如 现在进一步猜想:对应欧拉公式可能是对数函数与反正切函数的关系. 已知函数展开式 如果把对数函数展开式中的变量x换成ix后,展开式分成实部与虚部,就有 这样得到对应欧拉公式 假设微分方程 初始条件y|x=0=0时,解出y=ln(1+ix),所以f(x)=ln(1+ix),证毕. 另一证明 从等式出发 就有 应用换元法又有 分别积分得到 当x=0时,确定常数C=0,证毕. 对应欧拉公式的一般形式 设a,b,c为任意实数,且b≠0,a>0时,就有 证明 参考前面的证法,从略. 这种新的积分法值得进一步探讨. 现在探讨从欧拉公式推广到正弦函数与余弦函数推广. 设f1(x)=cosx,f2(x)=sinx,欧拉公式就是exp(ix)=f1(x)+if2(x).这一公式的由来是把exp(x)展开式中的x换成ix,然后把实部和虚部分开. 又有exp(jx)=F1(x)+jF2(x)+j2F2(x) . 由此得出F1(x),F2(x),F3(x)的微分方程组 初值条件F1(0)=1,F2(0)=0,F3(0)=0 . y1=exp(λ1x)=exp(-ix), 把y1,y2,y3相加除3得到 经验证y0适合上述微分方程及其初值条件的特解,所以y0=F1(x),对y0求一次导数得出F2(x),对y0求二次导数得出F3(x),这样得出F1(x),F2(x),F3(x)的初等函数表达式 函数组F1(x),F2(x),F3(x)具有下述重要性质. 性质1 展开为恒等式 性质2 应用矩阵乘法得出 F1(x+y)=F1(x)F1(y)-F3(x)F2(y)-F2(x)F3(y), F2(x+y)=F2(x)F1(y)+F1(x)F2(y)-F3(x)F3(y) , F3(x+y)=F3(x)F1(y)+F2(x)F2(y)+F1(x)F3(y) . 性质3 (F1(x)+jF2(x)+j2F3(x))n=F1(nx)+jF2(nx)+j2F3(nx), 其中,n为正整数. 性质4 exp(jx)=F1(x)+jF2(x)+j2F3(x) . 证明 从略(读者如有兴趣自行验证). 最后应该指出余弦函数f1(x)=cosx,正弦函数f2=sinx也有上述性质. 性质1′ 性质2′ 展开即得f1(x+y)=f1(x)f1(y)-f2(x)f2(y),f2(x+y)=f2(x)f1(y)+f1(x)f2(y) . 性质3′ 当n为正整数时,就有 (f1(x)+if2(x))n=f1(nx)+if2(nx). 性质4′ exp(ix)=f1(x)+if2(x). 由此可见,函数组f1(x),f2(x)与函数组F1(x),F2(x),F3(x)具有相同的上述性质,所以称函数组F1(x),F2(x),F3(x)为余弦函数f1(x)=cosx,正弦函数f2(x)=sinx的推广,或称三角函数推广. [1] 职济.数学娱乐(一)——夫妻问题的新证与应用[J].海南大学学报:自然科学版,2007,25(4):321-324. [2] 职济.数学娱乐(二)——牙牌问题的新证与推广[J].海南大学学报:自然科学版,2008,26(3):206-219. [3] 职济.数学娱乐(三)——洛书定理与应用[J].海南大学学报:自然科学版,2008,26(4):303-308. [4] 职济.数学娱乐(四)——Nasik幻方的性质与构造法[J].海南大学学报:自然科学版,2009,27(2):107-115. [5] 职济.数学娱乐(五)——推广Fibonacci数列与幂级数和[J].海南大学学报:自然科学版,2009,27(4):313-319. [6] 职济.数学娱乐(六)——移棋相间[J].海南大学学报:自然科学版,2010,28(1):1-10,14. [7] 职济.数学娱乐(七)——一个麻将和牌问题[J].海南大学学报:自然科学版,2010,28(2):92-98. [8] 职济.数学娱乐(八)——易经卦象的起源与考古发现的奇字[J].海南大学学报:自然科学版,2011,29(2):99-103. [9] 职济.数学娱乐(九)——学习《九章算术》的收获[J].海南大学学报:自然科学版,2011,29(4):297-304. [10] 职济.数学娱乐(十)——学习《九章算术》的收获[J].海南大学学报:自然科学版,2012,30(2):95-102. [11] 职济.数学娱乐(十一)——幻方与线性代数[J].海南大学学报:自然科学版,2012,30(4):299-305. [12] 职济.数学娱乐(十二)——广义华林公式与应用[J].海南大学学报:自然科学版,2013,31(1):1-7. [13] 职济.数学娱乐(十三)——类似华林公式的新公式[J].海南大学学报:自然科学版,2013,31(2):93-99. [14] 职济.数学娱乐(十四)——圆组合新概念与圆组合恒等式[J].海南大学学报:自然科学版,2014,32(1):1-7. [15] 职济.数学娱乐(十五)——从三角函数公式到伯努利数和欧拉数[J].海南大学学报:自然科学版,2014,32(4):205-301. [16] 职济.数学娱乐(十六)——移棋相间问题与国际科研成果[J].海南大学学报:自然科学版,2015,33(3):197-203. [17] 职济.数学娱乐(十七)——黎族数字[J].海南大学学报:自然科学版,2016,34(3):199-202. [18] 唐祐华.二元齐次对称多项式与二项式定理[M]杭州:浙江大学出版社,2012,217-225. Mathematical Recreation (XVIII): Three Questions of Higher Mathematics Geng Ji (Hainan University, Haikou 570228, China) The report includes three parts. The first part is equivalent Leibniz theorem, the second part is corresponding Euler formula, and the third part is the extension of trigonometric function. equivalent Leibniz theorem; corresponding Euler formula; the extension of trigonometric function 2016-06-01 耿济(1929-),男,江苏镇江人,海南大学(退休)教授 1004-1729(2017)01-0001-06 O 172 A DOl:10.15886/j.cnki.hdxbzkb.2017.00012 对应欧拉公式





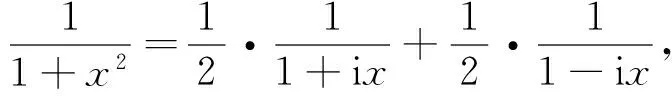
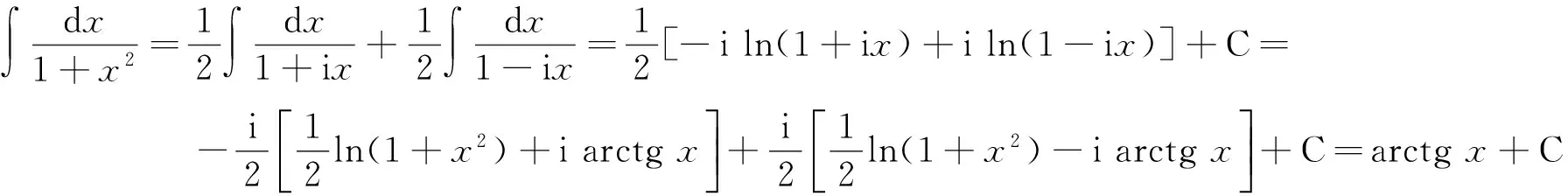
3 正弦函数与余弦函数推广




