连接性能对组合框架抗倒塌性能的影响*

高山 郭兰慧 张素梅

(1.重庆大学 土木工程博士后流动站， 重庆 400045； 2.西京学院 陕西省混凝土结构安全与耐久性重点实验室， 陕西 西安 710123； 3.哈尔滨工业大学 土木工程学院， 黑龙江 哈尔滨 150090)

在框架结构体系中，框架柱是主要的竖向承重构件，因此框架柱的失效也极易从局部破坏发展为结构的整体破坏或连续性倒塌.结构抗连续倒塌性能的研究一直是各国学者关注的重点，包括对结构体系的研究和梁柱节点性能的研究.在研究的基础上各国也制定推出了多部抗连续倒塌设计规范，获得广泛认可的规范主要有美国的DOD[1]规范和GSA[2]规范

根据失效位置，框架柱的失效大致可以分为边柱失效和内柱失效.由于失效位置不同，柱失效后的剩余结构承担附加荷载的承载机制也不同.除了梁本身的抗弯机制，边柱失效后结构主要通过各楼层间的组合作用承载，而内柱失效后结构主要通过与失效柱相连的梁的悬索机制承载.无论何种承载机制，梁柱连接均是保证内力重新分配的关键构件，其性能会对剩余结构的承载能力带来显著的影响.

通常采用试验的方式进行结构抗连续倒塌性能的研究最为有效，如文献[3]进行的一榀三层混凝土平面框架结构在中柱失效后的抗连续倒塌试验，揭示了平面框架连续倒塌过程的各个阶段及其特征.很多学者[4- 10]针对混凝土节点、钢节点和组合节点进行了试验研究，分析了空间效应、悬索效应和压拱效应对于结构抗倒塌性能的影响.文献[11]中提出将复杂的多高层结构简化为较为简单的单层结构，将失效跨周围的构件均当做弹簧边界条件，最终将结构由一个复杂的高层建筑简化为由弹簧边界进行约束的梁构件进行研究.也有一些学者[12- 15]采用有限元模拟的方法提出了结构体系抗连续倒塌的设计建议.文献[16]针对简化后考虑端部水平和转动弹簧的双跨钢梁，推导了其在均布荷载作用下的荷载位移相关公式，分析了连接刚度对于双跨钢梁竖向承载能力的影响.

文中针对梁柱连接性能对框架结构体系抗倒塌性能影响的研究存在的不足，基于已有研究成果，建立了三层钢-混凝土组合框架有限元模型，并与前期进行的试验进行了验证；对其进行动力拆柱分析，分别研究连接刚度和连接强度对于组合框架抗倒塌性能的影响，并提出了梁柱连接抗倒塌设计建议.

1 半刚性连接的定义

通常在框架设计中，梁柱连接节点会被简化为理想的刚接或者铰接.虽然刚接节点具有承载力高、刚度大等优点，但实践表明，从抗震角度来说，当框架结构采用具有一定柔性的节点时，可增加结构阻尼、延长周期、降低振幅，从而降低震害.

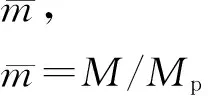
(1)

式中,M为连接承受的弯矩,Mp为梁的塑性弯矩.

(2)

θp=Mp/ib

(3)

式中,θr为梁柱的相对转角,θp为连接参考塑性转角,ib为梁的线刚度.

图1 EC3中连接分类的定义Fig.1 Definition of connection type in EC3

衡量连接半刚性的参数是连接相对刚度，即图1中的曲线斜率k，

(4)

连接相对刚度k为0.5的曲线是铰接与半刚接的分界线，k为25的曲线是半刚接与刚接的分界线.

同时，EC3[17]根据连接的承载能力将其分为铰接连接、全强度连接和部分强度连接.当连接承载力Mj不小于梁的承载力Mp时，将其定义为全强连接；当连接的承载力小于0.25Mp时，则将其称之为铰接连接；介于两者之间的为部分强度连接.文中将分别针对连接刚度和强度对组合框架抗倒塌性能的影响进行分析.

2 有限元模型的建立与验证

2.1 有限元模型概述

设计了3层4跨的钢-混凝土平面组合框架，如图2所示.其中柱脚处均为固结，框架结构的跨度均为7.5 m，层高均为3 m.

图2 模型尺寸(单位：mm)Fig.2 Dimensions of model(Unit：mm)

结构中采用Q345级钢材，楼板采用C30的混凝土，板中钢筋为A252型预制钢筋网片(直径8 mm，50 mm×50 mm网格，强度460 MPa).钢梁均采用W21×50型热轧型钢，钢柱均采用W14×193型热轧型钢，型钢截面的详细尺寸如表1所示.楼板采用120 mm厚混凝土板，混凝土翼板的有效宽度取1 600 mm.

表1 型钢截面尺寸Table 1 Dimensions of steel profile mm

采用通用有限元软件ABAQUS建立分析模型，采用Beam单元(B31)和Shell单元(S4R)对钢框架和混凝土板进行模拟，混凝土板中的钢筋采用Rebar Layer单元进行模拟.混凝土板和钢梁之间的组合作用采用*Tie命令进行模拟，保证两者之间无滑移，实现完全剪力连接，不再对抗剪连接件单独进行模拟.梁柱节点采用Hinge单元进行连接，该连接单元可以通过设定弯矩-转角曲线来模拟不同刚度的梁柱连接.

钢材材料本构采用两折线理想弹塑性模型，强化段模量取0.01Es；混凝土材料本构采用《混凝土结构设计规范》(GB 50010—2010)附录中给出的应力-应变关系(包括受拉和受压的本构关系).建立的有限元分析模型如图3所示.

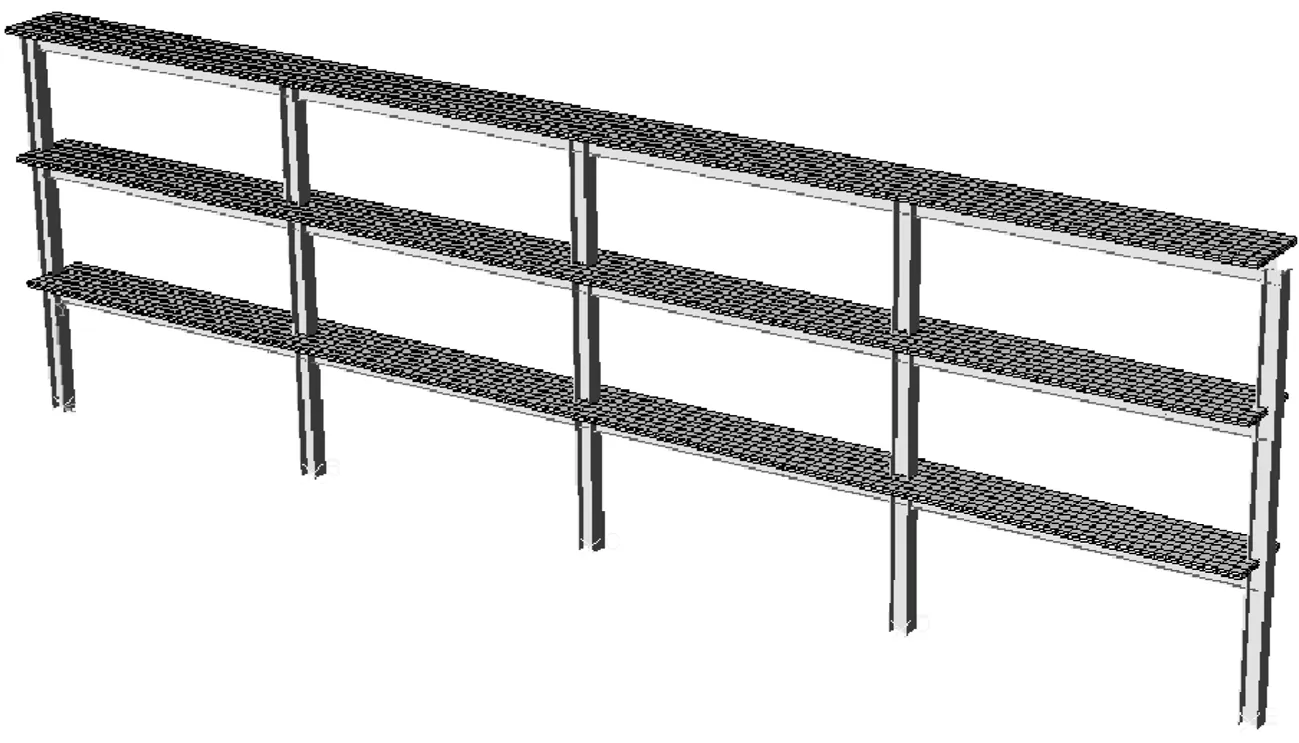
图3 框架有限元模型Fig.3 Finite element model of the frame

2.2 分析方法

采用拆柱法对结构进行抗倒塌动力分析，具体的做法是：首先在一定的时间内拆除某个位置的柱，再观测直接影响区和间接影响区结构在柱失效后的动力响应，以研究不同位置柱的破坏对结构抗倒塌性能的影响.文献[1]中规定在进行结构的动力拆柱分析时，构件的失效时间不得大于结构自振周期的1/10，根据结构的自振周期取构件的失效时间为20 ms，在拆柱完成后附加3 s的时间让结构的振动趋于稳定.

从经济角度和实用性方面考虑，根据文献[4]提供的针对新建或已建大型建筑进行抗倒塌设计时所选取的荷载组合对模型施加荷载并进行分析.在进行非线性动力分析时，在结构各楼层上施加的荷载组合均为结构的恒荷载加0.25倍的活荷载.

2.3 模型验证

为了验证有限元模型在单元选取和建模方法上的正确性，进行了一榀单层四跨的组合框架的抗倒塌试验[18]，并观测了中柱破坏后组合框架在竖向连续加载的过程中的抗倒塌性能.

根据文献[18]中采用的试件尺寸和相关参数建立相应的有限元模型，图4为试验结果与模拟结果的对比，模型中虽然由于Beam单元和Shell单元在几何形状上的限制，无法对试验中所出现的“压拱效应”进行有效模拟，但模型对初始刚度、塑性承载力以及后期悬索阶段性能的模拟效果均较好，可见模型的单元选取和建模方法均具有可靠性.

图4 有限元模型验证Fig.4 Validation of FE model

3 连接刚度的影响

假设半刚接节点能够传递的弯矩与组合梁相同，均为Mp，通过改变节点的初始转动刚度ki，构造出一组半刚接节点的弯矩-转角关系曲线S1-S5，曲线的初始转动刚度ki依次降低，如图5所示.其中折线OAF代表S1，折线OBF代表S2，…，折线OEF代表曲线S5，两条虚线分别代表刚接和铰接连接的刚度.

图5 弯矩-转角关系曲线(初始刚度)Fig.5 Moment-rotation relationship(initial stiffness)

根据刚性、半刚性和铰接连接的初始转动刚度的分界线，取ki为0.1模拟铰接连接，分别取ki等于2、5、10、15、20模拟半刚性连接，均匀分布在刚接和铰接之间的刚度范围内.对采用不同梁柱连接刚度的3层组合梁平面钢框架进行动力拆柱分析.

图6为连接刚度对失效点竖向最大位移的影响.由于在任意连接刚度下A3柱失效后结构均不能继续承载，图6(a)中并未显示连接刚度对A3柱的影响，这是由于虽然边跨柱失效无法形成悬索作用，但上下层边跨梁柱可以组成桁架体系承载，即“空腹效应”，而且A3柱失效后无论连接刚度如何，单独的悬臂梁也无法继续承载.

当边柱轴线A上的其他柱失效时，随着连接刚度的增大，失效柱上方的最大位移逐渐减小，并且A1柱和A2柱失效时节点的竖向位移基本相同.当连接刚度为0.1，即铰接连接时，无论是A1柱失效还是A2柱失效，节点位移均趋向无穷大，结构无法继续承载，可见连接铰接时结构边跨的抗倒塌能力极低.而当连接刚度在EC3规定的半刚性连接范围内时，即使刚度较低，结构也可在振动后稳定.

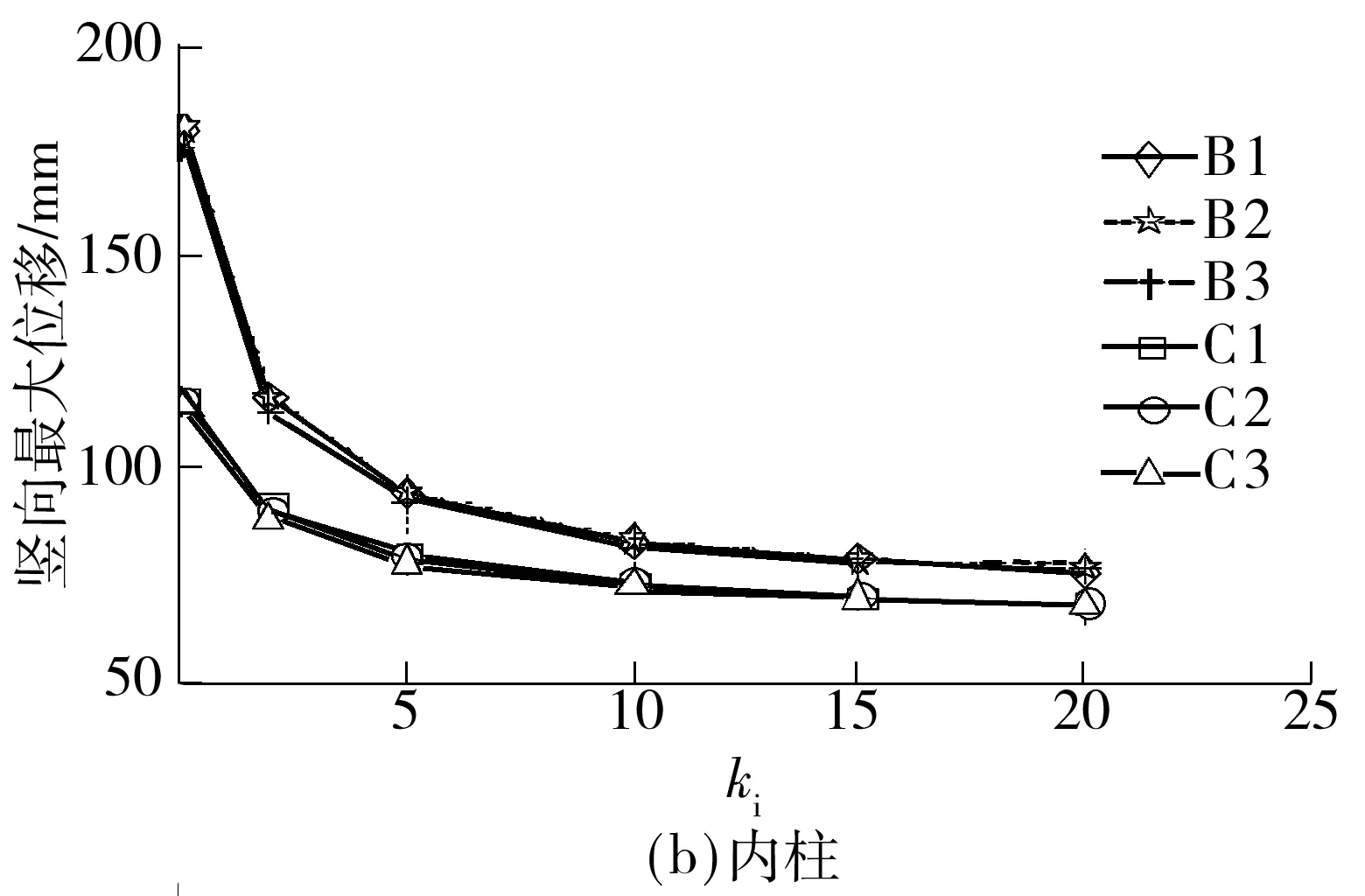
图6 连接刚度对最大竖向位移的影响

Fig.6 Influence of initial stiffness on max imum vertical displacement

由图6(b)可以看到:在不同连接刚度下，轴线B和轴线C上的各柱失效时，节点位移同样随着连接刚度的增加而减小；在同一轴线上，各层柱失效后的节点位移基本相同，可见连接刚度不会影响各层承载的独立性，由此可推断当荷载相同、跨度相同以及梁截面相同时，各层间并不会出现拉接力的作用，而是独立承担自身的荷载，此时不需要对层间柱进行过多设计，但当各层的荷载不同或各层梁的属性不同时，需要对层间的柱进行单独的拉结设计；轴线B上的节点位移要大于轴线C，可见在结构中，除边柱外，最不利的位置为与边柱相邻轴线上的柱，这是由于内部的梁均存在悬索作用，而越靠近边柱，梁两侧的拉结条件越不利，即水平约束刚度降低，不利于悬索作用的发挥.

同时由图6(a)、6(b)可以注意到，连接刚度对轴线A上的节点位移影响较明显，当ki从2增大至20时，节点位移减小了约60%；而在轴线B和轴线C上的节点，当连接刚度在半刚性范围内时，对于节点位移的影响则较轴线A小，分别为34%和25%.对于边柱和内柱，在柱失效后结构的承载机制不同，对于依靠层间组合作用承载的边柱，连接刚度的影响较大，否则层间将无法形成组合作用，而对于依靠悬索作用承载的内柱，边界约束条件将会直接影响节点位移，连接刚度越大，则直接影响区域对于边界约束条件的依赖越低，失效点位移就越小.

图7为连接刚度对节点上方柱的最大轴力的影响，可以看到连接刚度对节点上方的轴力影响均不大，最大轴力均保持在较低的水平，可见在任意连接刚度下，直接影响区域内层间柱均不会产生太大轴力，即对于内柱来说，在任意刚度下，各层间均是独立承担该层的荷载，而对于边柱，虽然各层是通过层间的组合作用来共同承担荷载，但组合作用通过柱端剪力来传递，因此层间柱中的轴力变化同样不大.

图7 连接刚度对上方柱最大轴力的影响

Fig.7 Influence of initial stiffness on maximum axial force in column

图8为连接刚度对于失效点两侧梁中最大轴力的影响.当边柱失效时，由于并无明显的悬索作用，因此梁中轴力较低，而连接刚度对于梁中轴力的影响也较小，连接刚度从2增大至20时，梁中轴力增大了13%，这是由于连接刚度越大，直接影响区域的结构可以更好地形成桁架体系来进行承载.而内柱失效时，连接刚度对于轴力的影响则相反，连接刚度的增加会明显降低梁中轴力，连接刚度从0.1增大至20时，梁中轴力降低了约30%，这是由于连接刚度的增加会减小直接影响区域的变形，从而使悬索作用减弱.由于轴线B处的节点位移较大，因此其直接影响区域的梁中轴力也要略大于轴线C处的梁，但随着连接刚度的增大，两者的差距逐渐减小，这是由于随着刚度的增大，梁的承载机制由悬索作用向受弯机制转换，边界条件对于承载机制的影响逐渐减小.

图8 连接刚度对两侧梁中最大轴力的影响

Fig.8 Influence of initial stiffness on maximum axial force in beam

图9为边柱失效时连接刚度对失效柱上方柱端最大剪力的影响，可以看到随着连接刚度的增加，柱端剪力逐渐增加并趋于稳定，可见连接刚度的增加使边跨各楼层间的组合作用增强，进而在柱端产生了更大的剪力.当首层柱A1失效时，柱A2和A3均承担层间剪力作用，连接刚度ki大于10后，柱端剪力则变化不大，并且第2层柱端剪力要大于第3层；而当第2层柱A2失效时，由于仅由第3层柱A3承担层间剪力，因此其荷载值较大，同时受刚度影响更加明显.

图9 连接刚度对边柱柱端最大剪力的影响

Fig.9 Influence of initial stiffness on maximum shear force in side column

图10为连接刚度对与失效跨相邻的梁中最大轴力的影响.可以看到，与失效跨内梁中拉力的变化趋势类似，随着连接刚度的增加，临梁轴力逐渐减小.但邻跨梁的轴力受连接刚度的影响较大，当连接刚度从0.1增加至20时，邻梁的最大轴力减小了约50%，可见在连接刚度较小时，应考虑邻跨梁所承担弯矩和拉力的共同作用.在相同连接刚度下，边柱失效后其邻跨梁轴力要大于内柱失效时，虽然边柱失效后无法有效形成悬索作用，但层间的组合作用依旧在邻跨梁中产生了较大轴力.

图10 连接刚度对邻跨梁最大轴力的影响

Fig.10 Influence of initial stiffness on maximum axial force in adjacent beam

4 连接强度的影响

取连接刚度ki=10的半刚性节点，并通过改变节点的抗弯承载力，构造出一组半刚接节点的弯矩-转角关系曲线M1-M3，曲线的抗弯承载力Mi依次降低，如图11所示.根据欧洲规范EC3中的定义，分别取梁柱连接承载力为0.25Mp、0.50Mp和0.75Mp.

图11 弯矩-转角关系曲线(承载力)Fig.11 Moment-rotation relationship(strength)

图12为连接强度对失效点最大位移的影响，图中并未包括轴线A上3层柱拆除后相应节点的最大位移，这是由于在所选用的3种连接强度下，轴线A上的3根边柱A1、A2和A3分别拆除时，程序均不收敛，竖向位移均趋向于无穷大，可见当连接强度小于组合梁强度时，边柱轴线上的柱破坏，无论位于哪个楼层，结构均会发生倒塌破坏.

图12 连接强度对失效点最大竖向位移的影响

Fig.12 Influence of connection strength on maximum vertical displacement of failure point

而对于轴线B和轴线C上的各层柱，可以看到位于同一轴线处的柱，当连接承载力相同时，各层节点位移基本相同，随着连接承载力的增大，节点位移逐渐减小.同时可以注意到，随着连接承载力的增加，轴线B和轴线C的柱移除后，相应节点位移逐渐接近，这是由于连接强度的增加可以减小在内力重分配过程中节点对于边界约束条件的依赖程度，可见对于边界约束条件较弱的节点，可以通过增强其连接强度来弥补边界约束条件的不足.

图13为连接强度对失效点上方柱最大轴力的影响，可以看到与刚度的影响类似，不同强度的连接同样不会对失效点上方柱的最大轴力产生太大影响，各楼层的结构构件之间依旧是独立工作承载.

图13 连接强度对失效点上方柱最大轴力的影响

Fig.13 Influence of connection strength on maximum axial force in the column over failure point

图14为连接强度对失效点两侧梁中最大轴力的影响，可以看到，随着连接强度的增加，梁中轴力下降，但下降的幅度并不大，可见连接强度对于梁中轴力的发展程度影响并不大，不如连接刚度的影响明显，这是由于梁中轴力的发展程度主要与结构的变形有关，而结构变形则主要受连接刚度的影响.而如图15所示，连接强度对于邻跨梁的最大轴力的影响则较为明显，随着连接强度的增加，临梁的最大轴力呈线性减小的趋势，这也证明了前文的结论，即连接强度的增加减小了内力重分布对边界约束条件的依赖.

图14 连接强度对失效柱两侧梁最大轴力的影响

Fig.14 Influence of connection strength on maximum axial force in beams connected to failure column

图15 连接强度对邻跨梁最大轴力的影响

Fig.15 Influence of connection strength on maximum axial force in adjacent beams

5 梁柱连接抗倒塌设计建议

(1)由于边跨柱失效时通过层间组合作用承载，因此在设计时要考虑柱底剪力对于柱身承载力的影响.而内柱失效时，若各层间荷载或结构梁不同，应考虑柱中附加轴力的影响.

(2)边跨梁柱连接的强度和刚度都将影响其层间作用的承载效果，在设计时应尽量避免在边跨使用刚度较低的半刚性连接以及强度比组合梁低的半刚性连接.

(3)连接自身性能和边界约束条件都会影响剩余结构的抗倒塌性能，因此越靠近边跨位置处的梁柱节点其边界约束条件越差，应适当加强其刚度或强度.

6 结论

文中采用ABAQUS建立了3层组合框架模型，对其进行了动力拆柱分析，重点分析了连接刚度和连接强度对于组合框架抗倒塌性能的影响，主要结论如下：

(1)连接刚度对于边跨空腹效应的影响要大于内跨悬索作用的影响，而连接强度直接决定了边跨空腹效应的形成;

(2)连接强度对于梁中轴力发展程度的影响不如连接刚度的影响明显，这是由于梁中轴力的发展程度主要与结构的变形有关，而结构变形主要受连接刚度的影响;

(3)连接刚度和强度的改变均不会影响各楼层间的独立承载，但当楼层荷载或结构梁发生改变时，则可能在层间柱中产生轴力;

(4)连接刚度和强度的增加都可以减小在内力重分配过程对于边界约束条件的依赖程度，对于边界约束条件较弱的节点，可以通过增强其连接强度来弥补边界约束条件的不足.

参考文献：

[1] Design of structures to resist progressive collapse:UFC 4- 023- 03—2009 [S].

[2] Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects:GSA—2003 [S].

[3] YI Wei-jian,ZHANG Fan-zhen,KUNNATH S K.Progressive collapse performance of RC flat plate frame structures [J].Journal of Structural Engineering，2014,140(9)：758- 782.

[4] YANG Bo,TAN Kang-hai.Experimental tests of different types of bolted steel beam-column joints under a central-column-removal scenario [J].Engineering Structures,2013,54(1):112- 130.

[5] YANG Bo,TAN Kang-hai.Behavior of composite beam-column joints in a middle-column-removal scenario：experimental tests [J].Journal of Structural Engineers,2014,140(2):04013045.

[6] YANG Bo,TAN Kang-hai,XIONG Gang.Experimental study about composite frames under an internal column-removal scenario [J].Journal of Constructional Steel Research,2016,121(1):341- 351.

[7] HOU Jian,SONG Li.Progressive collapse resistance of RC frames under a side column removal scenario：the mechanism of explained [J].International Journal of Concrete Structures and Materials,2016,10(2):237- 247.

[8] QIAN Kai,LI Bing,ZHANG Zhong-wen.Testing and si-mulation of 3D effects on progressive collapse resistance of RC buildings [J].Magazine of Concrete Research,2014,66(1)：1- 16.

[9] GUO Lan-hui,GAO Shan,WANG Yu-yin,et al.Tests of rigid composite joints subjected to bending moment combined with tension [J].Journal of Constructional Steel Research,2014,95(1)：44- 55.

[10] 霍静思,王宁,陈英.钢框架焊接梁柱节点子结构抗倒塌性能试验研究 [J].建筑结构学报,2014,35(4)：100- 108.

HUO Jing-si,WANG Ning,CHEN Ying.Experimental study on collapse resistance of welded beam-column connection substructure of steel frame based on seismic design [J].Journal of Building Structure,2014,35(4)：100- 108.

[11] IZZUDDIN B A,VLASSIS A G,NETHERCOT D A.Progressive collapse of multi-storey buildings due to sudden column loss(Part I)：simplified assessment framework [J].Engineering Structures,2008,30(5)：1308- 1318.

[12] 陆新征,李易,叶列平，等.钢筋混凝土框架结构抗连续倒塌设计方法的研究 [J].工程力学,2008,25(SupⅡ):150- 157.

LU Xing-zheng，LI Yi，YE Lie-ping，et al.Study on design method to resist progressive collapse for reinforced concrete frames [J].Engineering Mechanics,2008,25(SupⅡ):150- 157.

[13] 钱稼茹,胡晓斌.多层钢框架连续倒塌动力效应分析 [J].地震工程与工程振动,2008,28(2):8- 14.

QIAN Jia-ru，HU Xiao-bin.Dynamic effect analysis of progressive collapse of multi-story steel frames [J].Journal of Earthquake Engineering and Engineering Vibration,2008,28(2):8- 14.

[14] LI Ling,WANG Wei,CHEN Yi-yi,et al.Experimental investigation of beam-to-tubular column moment connections under column removal scenario [J].Journal of Constructional Steel Research,2013,88(5)：244- 255.

[15] 孔祥雄,史铁花,程绍革.基于材料损伤和失效准则的钢结构在强震下倒塌模拟分析方法 [J].土木工程学报,2014,47(9):38- 44.

KONG Xiang-xiong,SHI Tie-hua,CHENG Shao-ge.A numerical simulation method for steel structure collapse under rare earthquake based on the material damage and failure laws [J].China Civil Engineering Journal,2014,47(9):38- 44.

[16] 王开强,李国强,杨涛春.考虑悬链线效应的约束钢梁在分布荷载作用下的性能(I)——理论模型 [J].土木工程学报,2010,43(1):1- 7.

WANG Kai-qiang，LI Guo-qiang，YANG Tao-chun.A study of restrained steel beams with catenary action under distributed load(Part I)：theoretical model [J].China Civil Engineering Journal,2010,43(1):1- 7.

[17] Eurocode 3：Design of Steel Structure，Part- 1：General Rules and Rules for Building:BS EN 1993- 1- 8—2005 [S].

[18] GUO Lan-hui,GAO Shan,FU Feng.Structural performance of semi-rigid composite frame under column loss [J].Engineering Structures,2015,95(1):112- 126.