压电耦合智能板结构中微损伤识别方法研究

李 默

(江苏大学 理学院，江苏 镇江 212013)

压电耦合智能板结构中微损伤识别方法研究

李 默

(江苏大学 理学院，江苏 镇江 212013)

基于小波包能量谱分析方法，研究了压电耦合板结构中微损伤及其损伤程度的检测和识别方法。通过建立压电耦合板的谱有限元模型，数值模拟研究了金属板中微小凹陷损伤发生细微变化时传感器的动态响应；进而采用小波包分析技术对响应信号进行分解，得到一系列子信号的能量谱，分析了不同程度凹陷损伤对各节点能量谱的分布和幅值变化所产生的影响。研究结果表明，小波包能量谱能够对微小凹陷损伤及其损伤程度进行较为灵敏地识别，为实际检测工作提供了参考。

小波包能量谱分析；超声导波；压电晶片；谱有限元；微损伤

随着大型结构在航空航天、建筑、公路、桥梁以及机械领域的广泛应用。但由于结构在使用过程中极易出现损伤，如果未被及时发现，很有可能引发严重后果。因此，对结构早期微损伤进行实时检测和识别是尤为重要的，这不仅能降低结构的保养和维修成本，也能提高工程结构的服役寿命[1-3]。

由于结构的初期损伤比较细微，难以发现，且对结构动力学性能影响较小，导致给实时监测鞋困难。目前无损检测方法存在一定程度的不足，如固有频率法存在对损伤程度不敏感等缺点。

压电晶片具有结构简单、成本低以及易于小型化等优点，且可用较高激励频率，因此在微小损伤检测中显示出较大优势[4-7]。利用压电换能器不仅能在结构使用过程中及时有效地检测出损伤的存在，而且还能对损伤的性质和发展程度进行有效评估[8-12]。因此，结构损伤检测的关键在于构建与压电晶片相耦合的高频动力学结构模型和与之匹配的高精度损伤识别算法。

目前在对压电耦合结构进行理论建模过程中使用较广的是有限元法，虽然该方法在对复杂结构进行模拟时较解析法具有较大优势。但是在模拟高频导波在大型结构中传播特性时，往往需要较多的计算资源，且很难保证模拟精度。谱有限元的概念由Beskos于1978年第一次提出[13]，谱有限元在建模精度上较传统有限元有了大幅提高。而传统有限元方便灵活的建模优势在谱有限元上同样适用。因此，谱有限元方法相对有限元具有更大的理论优势和应用价值。

在对结构进行损伤识别，提取损伤信息时，传统用于识别损伤的参数，如固有频率等，受结构微损伤的影响小，所以识别精度较低。而小波分析能够对结构动态响应信号进行局部分析和细化的功能，能够更全面地揭示其他方法丢失的数据信息。但小波分析对信号高频部分的分解精度存在明显的不足。鉴于此，Mallat[14]在1988年提出了多分辨分析理论，多分辨分析在信号高频分析方面较小波分析有了一定的提升。此后， Wickerhauser和Coifman[15]于1992年提出小波包概念，作为一种更精细的信号分析方法，小波包分析通过频带的多层次划分对小波空间进行分解，实现了对多分辨分析理论无法对信号实现完全分解的高频成分进行了更为细致的分解，此外，小波包能量谱对结构微小损伤所引起的变化较为敏感，因此逐渐成为损伤检测领域的热点。石春香[16]等对简支梁模型的动力特性进行小波包分析，结果证明了小波包分析在梁结构的损伤识别中具有较高的灵敏度。崔王景[17]模拟了梁模型分别在两种载荷作用下的加速度响应，并对该响应进行了小波包分析，通过对信号在小波包分解下能量的相应变化率实现对梁模型中损伤的识别。

本文基于Mindlin板理论，利用谱有限元方法建立压电元件和板耦合的数值模型，模拟了压电元件在板结构中激励超声导波及接收相应的动态响应信号。并基于小波包分析技术，研究了结构在损伤前后的响应信号在小波包分解下各阶能量谱变化率，进而分析不同损伤程度对响应信号在小波包分解下各节点能量谱的分布和幅值变化所产生的影响，得到小波包能量谱变化特征和结构的损伤信息的对应关系。

1 压电耦合板结构的动力学模型

1.1 基板的动力学方程

基于Mindlin板理论，板的中性面的位移场u(x,y,z,t)，v(x,y,z,t)，w(x,y,z,t)可表示为

u(x,y,z,t)=-zθx(x,y,t)

(1a)

v(x,y,z,t)=-zθy(x,y,t)

(1b)

w(x,y,z,t)=w(x,y,t)

(1c)

式中，w(x,y,t)，θx(x,y,t)和θy(x,y,t)分别表示板的中性面上的横向位移、绕x和y轴的转角。

弯曲应变εb和剪切应变εs表达式为

εb={εxεyγxy}T=

(2a)

(2b)

对于各向同性材料，其应力-应变关系可以表示为

σb={σxσyτxy}T=Dbεb

(3a)

σs={τxzτyz}T=Dsεs

(3b)

式中，σb为弯曲应力；σs为剪切应力；Db和Ds为弹性矩阵，其表达式如下

(4a)

(4b)

其中，E和G分别为杨氏模量和剪切模量；μ为泊松比。

1.2 激励器和传感器的压电方程

压电晶片选取PZT-5A材料，当其作为激励器时，片内压电耦合关系表示为

σp=Qpεp-eTE

(5a)

e=dQp

(5b)

式中，σp和εp为应力场和应变场，由于PZT沿z向厚度很小，所以

(6a)

(6b)

当PZT与基板耦合时，由于PZT较薄，所以PZT片内的应变场εp与基板上表面弯曲应变εb近似一致，为εp=εb={εxεyγxy}T。

e和d为PZT的压电应力矩阵和应变常数矩阵。Qp为弹性矩阵

(7)

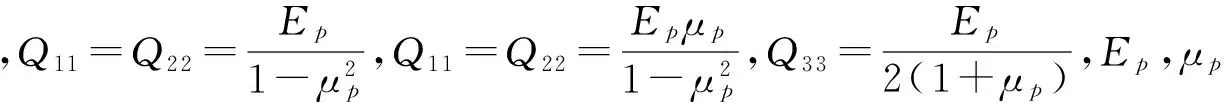
由于PZT仅在z向受外电场E3作用，所以外电场向量E为

(8)

对于作为传感器的PZT，其压电方程为

(9)

由于传感器受外电场E为0，所以有

D=eεp=dQpεb

(10)

1.3 压电耦合板结构的谱有限元建模

1.3.1Mindlin板谱单元的构建

基于Mindlin板理论，与其对应的二维谱单元中的插值基函数可以定义为

Nij(ξ,η)=hi(ξ)hj(η)

(11)

其中

(12)

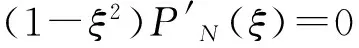
{u}={u v w}T=Nq=

(13)

其中，n1、n2分别为参考单元内ξ和η方向所确定的节点数;N为形函数矩阵;w0(ξi,ηj)、θx0(ξi,ηj)和θy0(ξi,ηj)分别为节点的横向位移、绕x和y轴的转角,i=0,1,2，…，n1；j=0,1,2，…，n2。

由位移场{u}可确定单元内的弯曲应变场εb和剪切应变场εs，可表示为

(14a)

(14b)

式中，Bb和Bs分别为板结构的弯曲应变-位移矩阵和剪切应变-位移矩阵，表达式为

(15a)

(15b)

对于Mindlin板单元，其在谱有限元中的单元刚度矩阵kb表示为

(16)

式中，Je为雅克比矩阵。

Mindlin板单元质量矩阵mb可以表述为

(17)

1.3.2 激励器和传感器的谱单元构建

对于和PZT片相耦合的激励单元和传感单元，PZT片所产生的附加单元刚度矩阵kp可以表示为

(18)

对于激励单元，PZT片产生的压电驱动力在单元每个节点的各个自由度上所产生的等效力为

(19)

对于传感器单元，其上的PZT片在波的驱动下所产生的电荷量为

(20)

2 信号分析和损伤信息提取

2.1 小波包分析理论

小波包分析通过对信号频带进行多层次划分，弥补了多分辨分析中信号高频分辨率不足的缺点，且提高了时频分辨率。

按照不同尺度因子j将空间L2(R)分解为子空Wj(j∈Z)正交和

L2(R)=⊕Wj(j∈Z)

(21)

其中，Wj为小波函数{ψj,k}k∈Z的小波子空间。

(22)

(23a)

(23b)

其中，gk(-1)khk-1，且两系数正交。

n=0时可得

(24a)

(24b)

推广到n∈Z+

(25)

由式(23)与式(24)所构造的序列{un(x)}(n∈Z+)称为由基函数u0(x)=φ(x)确定的小波包。

2.2 结构损伤信息提取

由于结构在含损伤前后的响应信号被小波包分解后，其波形往往不能直观地进行比对。所以，通过提取响应信号在小波包分解下的各频段的能量谱能够较好地反映结构中的损伤信息。

结构的响应信号R00(t)可以表示为

(26)

其中，Rkj(t)是响应信号R00(t)经过小波包分解后各个频段的子信号;k、j分别表示小波包分解树的具体层数和每一层中的节点序数。

其中每个频带对应子信号的能量表示为

(27)

所以板结构在存在损伤前后响应信号的每一阶子信号所含能量的变化量为

(28)

因此，所有子信号在结构损伤前后能量变化量可用向量表示为

Λ={Γ1,Γ2,…,Γ2k-1}

(29)

3 微损伤识别数值模拟

3.1 压电耦合板结构的数值模型

本文研究结构如图1所示，基板为铝材料，其尺寸为：长40cm，宽40cm，高1cm。A、B、C处分别为激励器、传感器和损伤所在位置。其中A、B尺寸相同，为长1cm，宽1cm，高0.1cm。A、B、C左下角顶点在xy面坐标分别为：(20cm,0cm)、(20cm,20cm)和(30cm,10cm)。

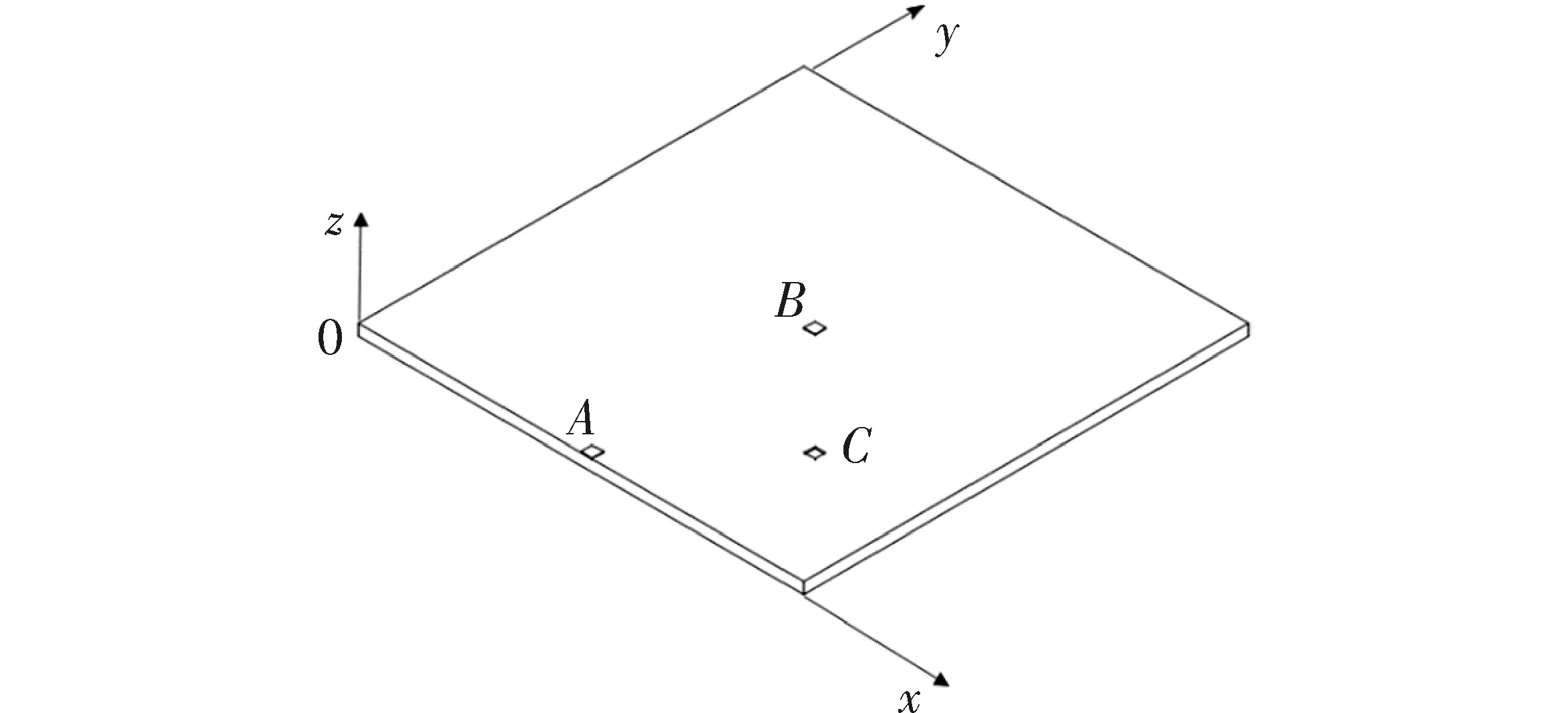
图1 压电耦合智能板结构示意图

本文模拟了板表面的凹陷损伤，并在损伤的相关特性发生微小变化的情况下对其逐一进行了模拟。具体损伤特性设定如下：

在图1损伤位置C处分别存在x、y方向的边长均为1cm，z方向深度分别为0.5cm、1mm、1.5mm、2mm、2.5mm、3mm、3.5mm和4mm的凹陷损伤。

通过对激励器A施加激励电压，其中心频率100kHz，幅值100V的汉宁窗调制的五峰波，波形如图2所示。通过传感器B来接收结构的动态响应信号。

图2 激励信号

3.2 基于小波包能量谱的损伤识别效果

本文分别对完整板结构和含损伤板结构模型进行模拟，得到各个结构传感器所接收到的电压响应信号作为结构的动态响应信号，再利用小波包分析对各响应信号进行分解，并求出各小波包节点所对应的能量谱，通过各损伤所对应结构的响应信号相对完整结构在小波包分解下的各阶能量谱的分布特征和幅值变化来对损伤程度和损伤特征进行识别。

本文选取DB6小波函数作为小波包分析的基函数，并对结构响应信号进行小波包分解，分解层次选为32。

各损伤结构所对应的动态响应信号在小波包分解下的各阶能量谱相对完整结构能量谱的变化百分比如表1所示。

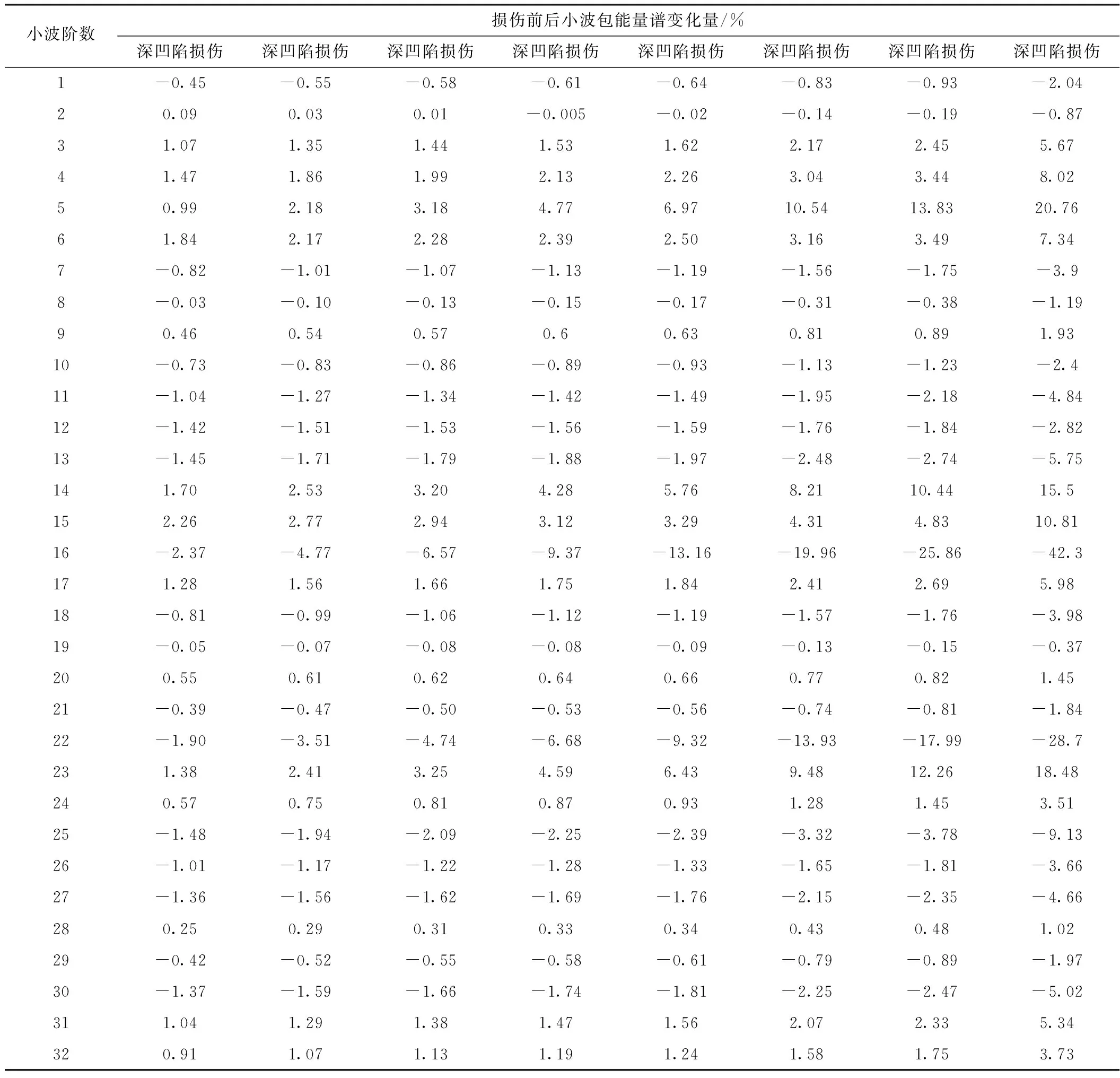
表1 损伤前后小波包能量谱变化量

从表1可以看出，小波包能量谱在尺度4、6、14、15、16、22、23和25处的变化幅度对0.5mm深凹陷损伤较为敏感，且变化幅度以中心尺度附近较大，向两边程逐渐递减趋势，尺度16处能量谱相对完整结构的变化幅值最大。1mm深凹陷损伤结构的能量谱相对完整结构变化幅度在尺度14、15、16、22和23处明显高于0.5mm深凹陷，且于尺度16处变化幅值达到最大。1.5mm深凹陷损伤结构所对应的能量谱在尺度5、14、15、16、22和23处幅值的变化程度显著高于能量谱在其他尺度的变化幅度，并于尺度16和22处的变化幅值相对1mm和0.5mm损伤结构有着较为显著的差异，和1mm和0.5mm损伤结构一样，2mm深凹陷损伤结构同样在尺度16处能量谱相对完整结构的变化幅度达到峰值。 深凹陷损伤结构的能量谱变化幅度的峰值依然出现在16尺度处，且于尺度5、14、16、22和23处的变化幅值较其他尺度变化幅值的差异程度较1.5mm深凹陷损伤更为明显，且在这几个尺度的变化幅值较含1.5mm深凹陷损伤结构同样具有显著差异。此后，2.5mm、3mm、3.5mm和4mm深凹陷损伤结构的小波包能量谱在尺度5、14、16、22和23处的变化幅值随损伤深度的不断增加逐渐增大，各个损伤在这几个尺度处能量谱变化幅值的差异同样较为明显，且都在尺度16处达到峰值。从表1的整体变化趋势可以看出，存在凹陷损伤的结构动态响应信号在小波包分解下的能量谱在尺度5、14、16、22和23处较完整结构能量谱的变化幅值对凹陷损伤的深度变化较为敏感，且在尺度16处各损伤结构对应的能量谱变化幅值存在最为显著的差异。

因此，小波包的各阶能量谱对板状结构中微小凹陷损伤较为敏感，并且随着损伤深度按 幅度发生递增时，能量谱的分布和幅值也出现较为显著的变化。所以，结构中的微小凹陷损伤及其损伤程度的相关信息可以由小波包能量谱直观地表征。

4 结束语

使用小波包分析技术，研究了板结构中微损伤及其损伤程度的检测和识别问题。通过动力学模型仿真分别得出结构存在微小凹陷损伤以及损伤程度发生细微变化的情况下结构中传感器的动态响应信号。用小波包分析法对响应信号进行分解，进而取得一系列子信号并求出其能量谱，通过与完整结构响应信号能量谱进行对比来研究微小凹陷损伤及其损伤程度对结构响应信号能量谱的分布和幅值变化所产生的影响，得到小波包能量谱变化特征和结构的损伤信息的对应关系。

研究表明，将结构响应信号的小波包能量谱作为损伤检测的特征量，具有更高的灵敏度。不仅能检测到板结构中存在的微小凹陷损伤，而且当损伤的特性和程度发生细微变化时亦能很好地识别。

[1] 宋天民.无损检测新技术[M].北京:中国石化出版社,2012.

[2] 张俊哲.无损检测技术及其应用[M].北京:科学出版社, 2010.

[3] 宋天民.超声检测[M].北京:中国石化出版社,2012.

[4]LinX,YuanFG.Diagnosticlambwavesinanintegratedpiezoelectricsensor/actuatorplate:analyticalandexperimentalstudies[J].SmartMaterials&Structures,2001,10(5):907-913.

[5]VeidtM,LiuTR,KitipornchaiS.Flexuralwavestransmittedbyrectangularpiezoceramictransducers[J].SmartMaterials&Structures,2001,10(4):6481-6492.

[6]VeidtM,LiuT,KitipornchaiS.Experimentalinvestigationoftheacousto-ultrasonictransfercharacteristicsofadhesivelybondedpiezoceramictransducers[J].SmartMaterials&Structures,2000(9):19-23.

[7]MoulinE,AssaadJ,DelebarreC.ModelingofLambwavesgeneratedbyintegratedtransducersincompositeplatesusingacoupledfiniteelementnormalmodesexpansionmethod[J].TheJournaloftheAcousticalSocietyofAmerica,2000,107(1):87-94.

[8]BenBS,BenBA,VikramKA,etal.DamageidentificationincompositematerialsusingultrasonicbasedLambwavemethod[J].Measurement,2013,46(2):904-912.

[9]KimSB,SohnH.Instantaneousreference-freecrackdetectionbasedonpolarizationcharacteristicsofpiezoelectricmaterials[J].SmartMaterialsandStructures,2007,16(6):2375-2387.

[10]ParkHW,HoonS,KinchoHL,etal.Timereversalactivesensingforhealthmonitoringofacompositeplate[J].JournalofSoundandVibration,2007,302(1-2): 50-66.

[11]OstachowiczW,KudelaP,MalinowskiP,etal.Damagelocalisationinplate-likestructuresbasedonPZTsensors[J].MechanicalSystemsandSignalProcessing, 2009,23(6):1805-1829.

[12]HuN,ShimomukaiT,FukunagaH,etal.DamageidentificationofmetallicstructuresusingA0modeofLambwaves[J].StructuralHealthMonitoring,2008,7(3):271-285.

[13]NarayananGV,BeskosDE.UseofdynamicinfluencecoefficientsinforcedvibrationproblemswiththeaidoffastFouriertransform[J].Computers&Structures,1978,9(2):145-150.

[14] 李大军.随机激励下桥梁结构损伤识别方法研究[D].北京:北京工业大学,2005.

[15]DaubechiesI,MallatS,WillskyAS.Specialissueonwavelettransformsandmultiresolutionsignalanalysis—introduction[J].IEEETransactionsonInformationTheory, 1992, 38(2):529-532.

[16] 石春香,李胡生,刘钰杰.桥梁预警系统中小波包能量变异极值指数预警指标的可行性研究[J].上海应用技术学院学报:自然科学版,2009,9(4):274-277.

[17] 崔王景.基于小波包能量方法的结构损伤识别应用研究[M].重庆:重庆交通大学,2010.

Research on Micro-damage Identification Method of Intelligent Piezoelectric Plate Ptructure

LI Mo

(School of Science,Jiangsu University,Zhengjiang 212013,China)

Based on the analysis technology of wavelet packet energy spectrum, the problem of micro damage and its degree detection in piezoelectric intelligent plate structure is studied in this paper. Numerical simulation is used to simulate the response signal of the structure containing micro groove damage with its degree changes. The response signal is decomposed by wavelet packet analysis to get a series of sub-signals and energy spectrums accordingly. The relationship between the distribution of energy spectrum and the degree of groove damage is researched. Research indicates that the wavelet packet energy spectrums can sensitively recognize the groove damage and its’ degree. The results can provide important guidance for real testing work.

wavelet packet energy spectrum;ultrasonic guided wave;piezoelectric wafer;spectral finite element;micro-damage

2016- 05- 13

国家自然科学基金(11172114)

李默(1989-)，男，硕士研究生。研究方向：压电超声无损检测。

10.16180/j.cnki.issn1007-7820.2017.04.002

TN304.9；O422

A

1007-7820(2017)04-005-06