给定电势导体球与极板体系的电势与电场

黄 爽，郭 伟，吴 娟，高 欣

(贵州大学物理学院，贵阳 550025)



给定电势导体球与极板体系的电势与电场

黄 爽，郭 伟，吴 娟，高 欣

(贵州大学物理学院，贵阳 550025)

用多重镜像法研究了在外加电场中给定电势的导体球和极板体系的电场分布、电势问题。给出了计算镜像电荷和偶极矩的理论推导和计算方法，通过得到的镜像分布，计算并讨论了空间电场分布，得到了球上电势与一阶镜像电量的关系，指出对于该体系，不能通过球的电势直接确定电量，而是应先用镜像法确定电势和电量的关系，再根据给定的电势确定电量，而后再应用镜像法计算和分析电荷、电场和电势分布。

导体球；镜像法；电势；电偶极矩；电场

球体在电场中的极化或静电感应，是很多研究领域的基本问题。导体球在外电场中发生静电感应，会导致电荷分布和空间电场发生改变，尤其是当导体球本身带电的时候，情况会变得更为复杂。球体在均匀电场中，电场分布有严格的解析解[1-2]。但当导体球接近极板时，极板上的电荷分布会受到导体球上电荷的影响。计算了导体球接近极板时的情况，对于给定电势的导体球，导体球上会带有电荷，应用球上所带的电荷量来确定球上的电势。实际上，当导体球接近极板的时候，球与极板之间的电场不再是简单的均匀电场和球的感应电场的叠加，因为极板上的电荷分布也发生了变化。此外，球与极板之间的电场，还取决于极板的电势。

从电动力学理论发展起来的镜像法被广泛采用来处理有对称性的导体球体系[3-5]，最早由Thomoson提出[6]。因为其物理图像清晰、计算精度高、计算速度快等优点，被普遍采用。很多研究者采用镜像法处理在外电场中两个接近的导体球的静电感应、电荷、电场分布及相互作用等问题[7-13]。对于给定电势导体球的研究工作较少。Bosch等人[14]指出，当球的电势给定为UB时，其带的电量可以用

(1)

来确定，再根据这个确定好的电量，用镜像法去求解电场分布。高欣等人[15]发展了多重镜像法，可以计算等电势导体球体系的电场分布，但并未涉及给定电势。

本文中，我们将基于多重镜象法，分析给定电势导体球靠近极板时，极板和球上的电荷分布，以及球和极板间的电场分布，澄清给定电势的导体球上电量对电势的依赖关系。

1 理论计算

考虑如图1所示的体系，极板A和C之间为均匀电场，电场强度由两个极板的电势确定。半径为R的导体球置于靠近极板A的位置，球面距极板距离为L，电势由外接电源给定。在这种情况下，无论极板电势还是电场强度改变，球上电势始终恒定。假设球上电量为q1，当不考虑外加电场时，由电势的唯一性原理可知，电荷均匀分布在球面，球外电场可看成球心位置处电量为q1的点电荷产生的电场。当导体球不带电时，在外加均匀电场中导体球发生静电感应，球外电场可以等效为位于球心的电偶极矩PB,1=4πε0R3E0，所产生的电场与均匀电场的叠加。

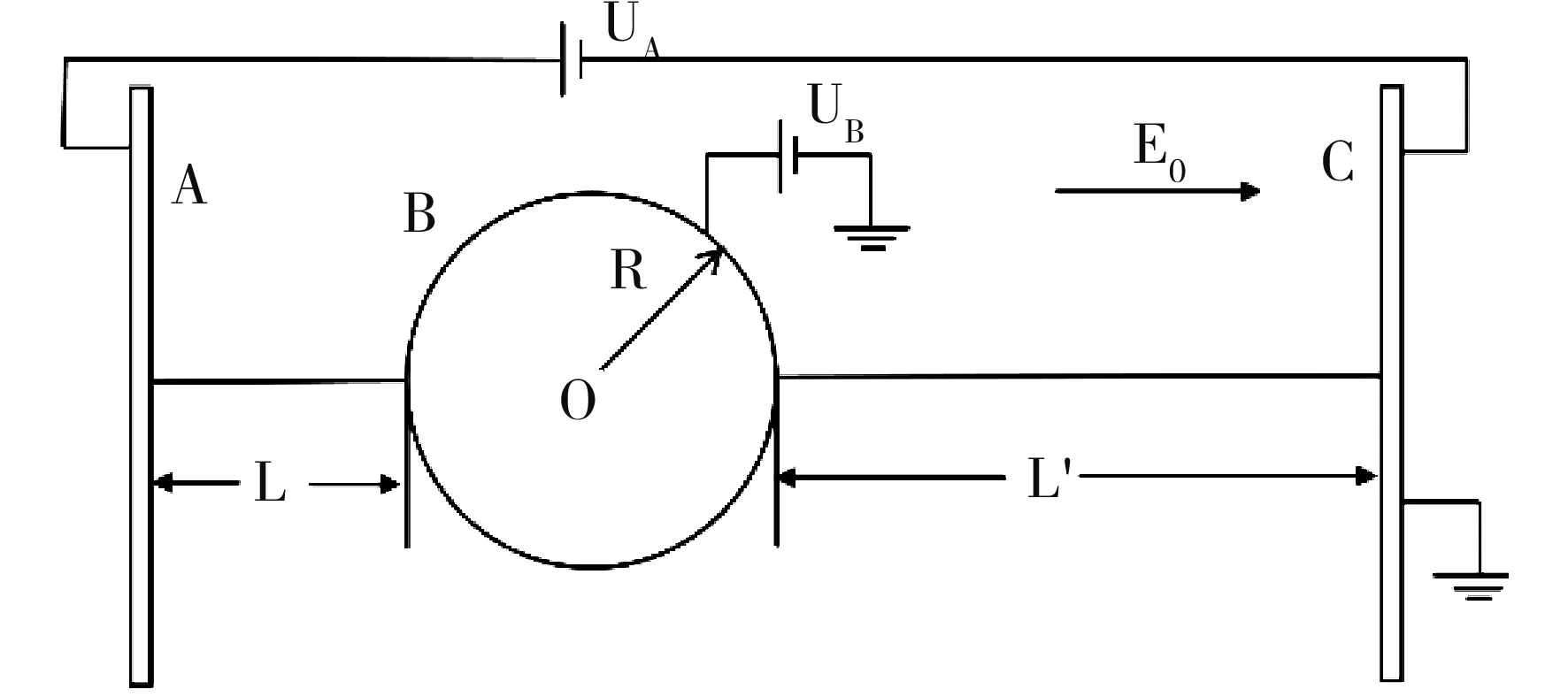
图1 均匀电场给定电势的导体球Fig.1 Conducting sphere in the given potential of uniform electric field

当球离极板较远时，球对极板上电荷分布的影响可以忽略。当球靠近极板时，球上的电荷又会影响极板上的电荷分布。这里只考虑较简单的情况，球靠近极板A，离极板C非常远，因此球上电荷分布对极板C的影响不需考虑，而仅考虑球对极板A的影响，如图2所示。假设均匀电场E0=105V/m，方向沿水平方向向右，极板A的电势为UA，导体球的半径R=3.15×10-3m，球面到极板A的最近距离L=2.5×10-2m，导体球的电势由接地电动势提供，恒定为UB。

根据无限大导体平面的镜象法理论[16]，点电荷q1在极板中的镜像电荷为到极板等距的异号电荷，相应的电偶极矩镜像为极板左侧相同距离处方向、大小都相同的电偶极矩。极板中镜像电荷又会在球内产生第二阶镜像[15]：

(2)

(3)

(4)

其中，d=L+R，是球心到极板的距离，rA,2是镜像电荷和偶极矩到球心的距离。电偶极矩在导体球内的镜像包括处于同一位置的一个电偶极矩和一个镜像电荷，式(3)中第二项为电偶极矩在球内产生的镜像电荷。同样，球内的二阶镜像电荷和偶极矩又会在极板产生二阶镜像，依次类推，可以得到各阶镜像电荷和偶极矩的通式。球内的第i阶镜像为：

(5)

(6)

(7)

其中，rB,i表示第i阶镜像到球心的距离。极板内的第阶镜像：

PA,i=PB,i

(8)

qA,i=-qB,i

(9)

rA,i=rB,i

(10)

其中，rA,i表示极板内第i阶镜像距离极板内第一阶镜像的距离。

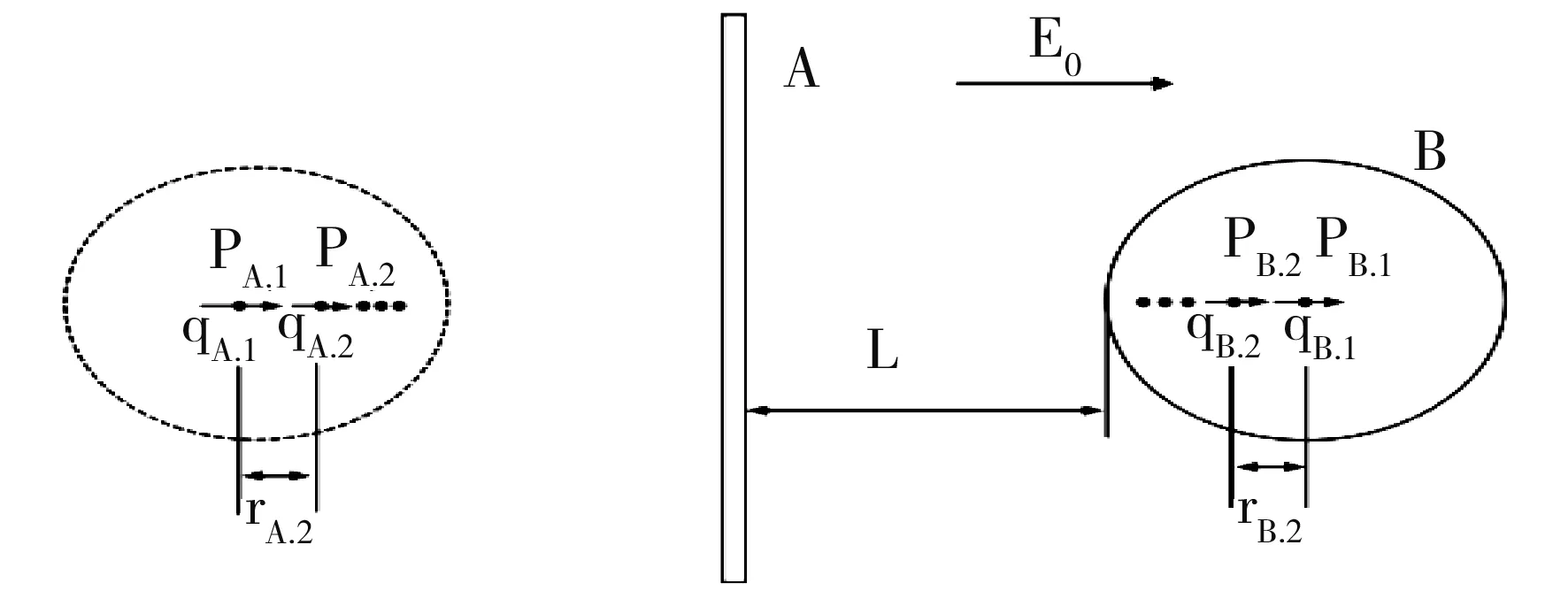
图2 镜像电荷分布Fig.2 Image charge distribution

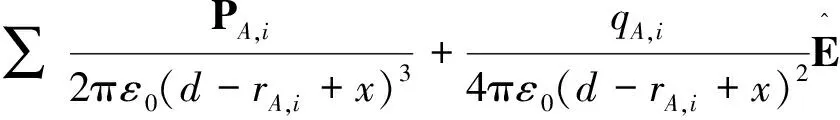
(11)

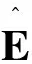
(12)

可求出导体球B上的电势。

2 计算结果及讨论

给定导体球上最初带有的不同电量，根据式(11)计算得到的极板与球之间轴线上的电场分布如图3所示。从图3 中可以看出，不管球上是否带电，以及带有何种电荷，靠近导体球位置电场强度都会增强。当球上带有负电荷时，电量越大，靠近球边缘电场强度越高。当电量足够大的时候，极板与球之间的电场都会有明显的增加。当电量减小为零，靠近球的位置电场方向依然为正，且有显著增强。电荷为正时，如果电量较小，球边缘电场强度并没有改变方向，而且依然有明显的增强。当正电荷的电量较大时，靠近球的电场强度会有电场方向的改变，也就是说，极板与球之间，电场强度先是接近没有球存在时的均匀正向电场的强度，离球越近，电场缓慢下降，直到为零，之后越靠近球，电场强度又迅速增加，且为反向电场。

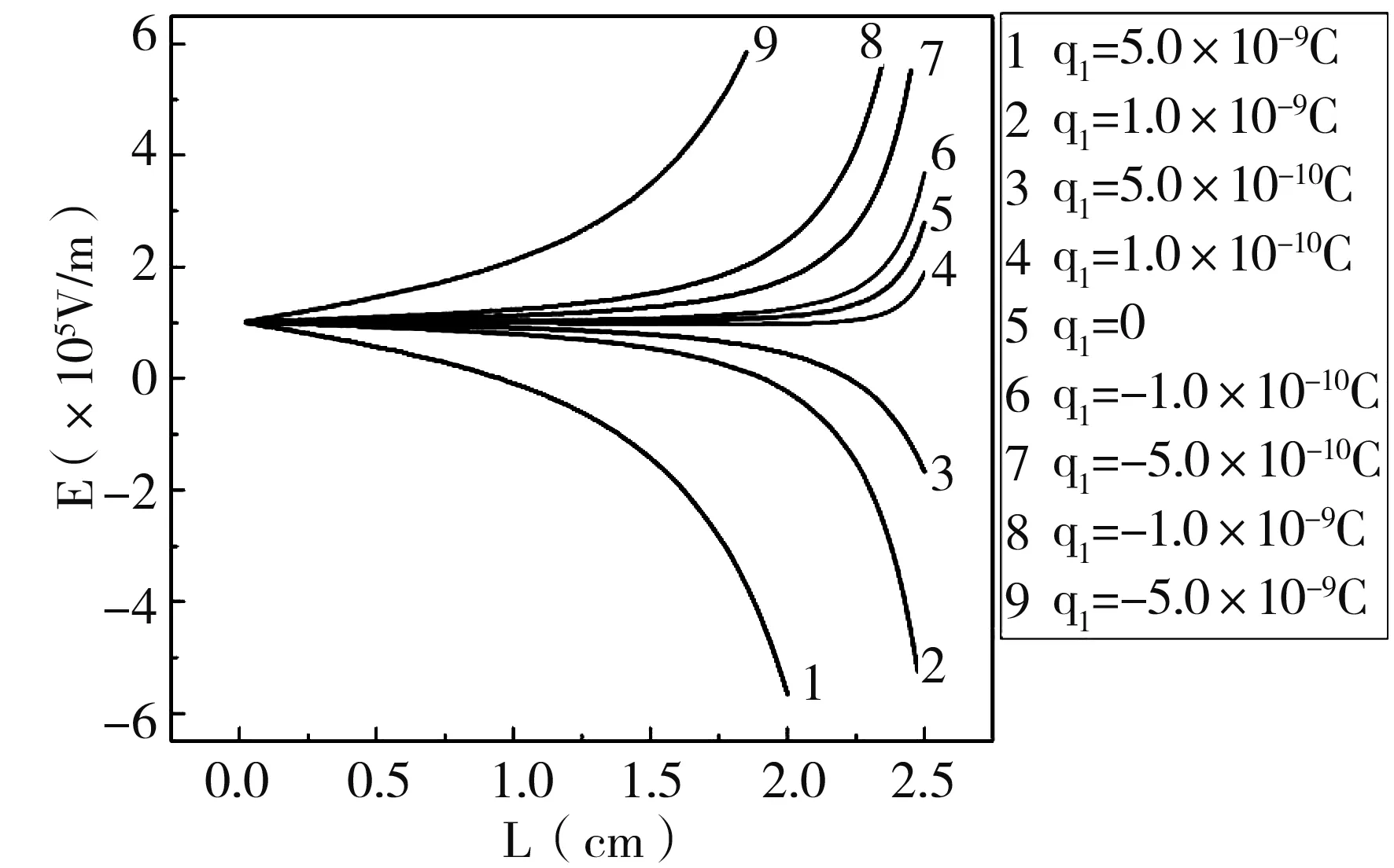
图3 导体球带不同电荷量时，极板与导体球间的电场分布Fig.3 The distribution of electric field between the plate and the conducting sphere when the charge volume of the conducting sphere is different

球上初始电量不同时，可以根据式(12)计算极板与导体球间相应的电势差，如图4所示。从图中可以看出，电势差与电量满足线性关系。对计算结果进行拟合，得到导体球电势跟电量的函数关系：

UB=2.534×1012×q1-2 814.4+UA

(13)

而如果用文献[14]中给出的公式(1)代入本例中相应的参数，则为：

UB=2.855×1012×q1-2 815+UA

(14)

对比发现，其对应的比例系数有本质的差别。可见，直接按照文献[14]中给出的方法，通过导体球上的电势来确定导体球的一阶镜像电荷，会导致错误的结果。相反，用镜像法处理这种给定电势体系，只能先根据体系参数，通过球上不同的一阶镜像电荷值，来计算球上的电势，再根据拟合公式，就可以确定导体球上给定电势其所相应的一阶电荷量。

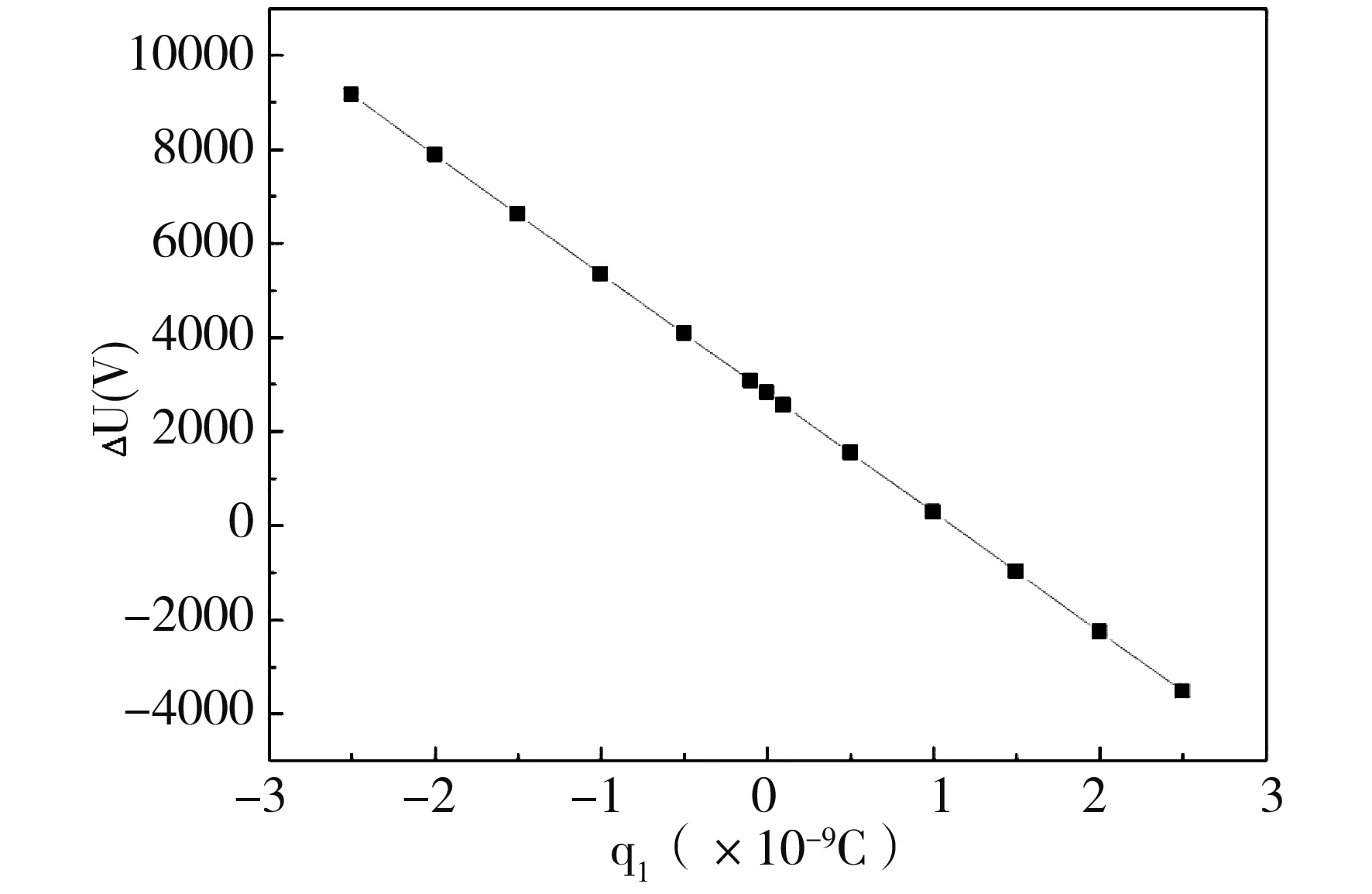
图4 极板与导体球之间的电势差随导体球带电量的变化关系Fig.4 The relationship of the potential difference between the plate and the conducting sphere with the charge amount of conducting sphere

3 结论

本文介绍了多重镜像法在极板与给定电势导体球体系中的应用，详细推导了多重镜像法的递推迭代公式。用得到的镜像分布求电场分布及导体球的电势，得到了导体球电势与球上一阶电量的函数关系。通过对比分析发现，直接用给定电势无法确定导体球上的一阶镜像，必须先根据给定体系的参数，通过镜像法给出电势与一阶镜像的函数关系，来确定一阶镜像的电量，再通过镜像法计算电荷分布、电场分布。

[1] 胡先权，廖海峰.电偶极子位于均匀介质球中时球外电场的研究[J].大学物理，2008，27(11)：20-23.

[2] 刘世明.从极化过程分析介质球在均匀电场中的场强分布[J].河南科学，2008，26(8)：907-909.

[3] W. E. Smith and J. Rungis,Twin adhering conducting spheres in an electric field-an alternative geometry for an electrostatic voltmeter [J].Journal of Physics E：Scientific Instruments，1975，(08)：379.

[4] J. C-E.Sten, K. I. Nikoskinen,Image polarization and dipole moment of a cluster of two similar conducting spheres [J].Journal of Electrostatics，1995，(35)：267.

[5] B.Techaumnata, T. Takuma,Electric field and force on a conducting sphere in contact with a dielectric solid [J].Journal of Electrostatics，2006，(64)：165.

[6] Thomson W. Reprint of Papers On Electrostatics and Magnetism[M]. Macmillan & Company，1872.

[7] L.Poladian,General theory of electrical images in sphere pairs[J].Quarterly Journal of Mechanics and Applied Mathematics，1988，(41)：395-417.

[8] D. J. Jeffrey，Y. Onishi.Electrostatic of two unequal adhering spheres[J].Journal of Physics A: Mathematical and General，1980，(13)：2847.

[9] A.Moussiaux, A. Ronveaux,Electrostatic capacity of two unequal adhering spheres[J].Journal of Physics A: Mathematical and General，1979，(12)：423.

[10] D. J. O’Meara, D. A.Saville,The electrical forces on two touching spheres in a uniform field [J].The Quarterly Journal of Mechanics，Appl Math ，1981， 34 (1)：9-26.

[11] J.Slisko，R. A. Brito-Orta,On approximate formulas for the electrostatic force between two conducting spheres[J].American Journal of Physics，1998，(66)：352.

[12] B. U.Felderhof, D. Palaniappan,Electrostatic capacitance of two unequal overlapping spheres and the rate of diffusion-controlled absorption[J].Journal of Applied Physics，1999，(86)：6501.

[13] G.Tong,Electrostatics of two conducting spheres intersecting at angles[J]. European Journal of Physics，1996，(17)：244.

[14] H.F.M.van den Bosch，K.J.Ptasinki,and P.J.A.M.Kerkhof,Two conducting spheres in a parallel electric field[J].Appt.Phys.，1995，(78)：6345-6352.

[15] X.Gao，Q. Wang，G. Sun，C. X. Li，L. Hu, Two identical conducting spheres with same potential in a uniform electric field[J].Journal of Electrostatics，2015，(77)：88-93.

[16] 郭硕鸿. 电动力学[M]. 北京：高等教育出版社，1997：53-56.

[17] Xin G，Lin H，Gang S. Multiple Image Method for the Two Conductor Spheres in a Uniform Electrostatic Field[J]. Communications in Theoretical Physics，2012，57(6)：1066.

The potentials and electric field distribution of the system including an electrode and a conducting sphere with fixed potential

HUANG Shuang, GUO Wei, WU Juan, GAO Xin

(College of Physics, Guizhou University, Guiyang 550025, China)

The multiple image charge method has been used to study the potential and electric field distribution of the system including an electrode and a conducting sphere with fixed potential. The theoretical derivation and calculation of the image charges and dipole moments for this system has been provided. After the image distribution was determined, the electric field can be calculated using all image charges and dipole moments. The relation between the potential of the sphere and the first order image charge has been given. We point that the first order image charge on the conducting sphere must be determined by the relation equation that was calculated by image method considering the parameters used in the system.

Conducting sphere; Image charge method; Potential; Electric dipole moment; Electric field

2016-10-25

国家自然科学基金(11304049)；贵州大学博士基金(贵大人基合字(2012)020号)

黄爽(1992-)，女，硕士研究生在读。

高欣，e-mail：gaoxin0526@163.com。

O441

A

1674-8646(2017)02-0044-03