一种改进的SVM增量学习算法研究

黄建校　邵曦

摘要：通过对训练样本集的几何特征和机器学习迭代过程中支持向量的变化情况分析，文章提出一种改进的基于KKT条件和壳向量的SVM增量学习算法。算法使用包含原支持向量集的小规模扩展集——壳向量，将其作为新一轮迭代的初始训练样本集。同时，基于样本是否违背KKT6件的错误驱动策略，对新增的大量样本进行筛选，以此得到更加精简有效的新增样本集。实验结果表明，与传统的增量学习算法相比，改进的算法在模型训练的收敛速度和对未知样本集的分类准确度方面都有明显的提高。

关键词：SVM；壳向量；KKT条件；增量学习

1.SVM算法研究背景

随着互联网时代和多媒体信息技术的飞速发展，大量的网络资源也随之产生，其中也包括受众面非常广泛的数字音乐。面对数量庞大和风格多样的数字音乐，一个非常重要的需求是准确而快速地查询出符合用户喜好的音乐。为此，人们需要设计一个高效快速的音乐分类系统。

针对音乐分类，许多研究者已经提出了各自的方法，大体可以分为3类：一是在音乐特征提取的选择和特征向量的维度上作改进；二是在分类算法的选择上作改进；三是在多分类问题的解决方法上作改进。其中，研究最多的是对分类算法的改进。而在这些研究当中，应用最为广泛的技术就是支持向量机（Support Vector Machine，SVM）。

虽然经典的SVM算法应用广泛，但其依然存在一定的局限性。由于SVM是一种监督式的学习算法，它不具备增量学习的能力，只能使用少量给定的己标注的样本作为训练样本进行训练，以此来得到分类模型。然而，在现实应用中，数字音乐的数据量通常呈现出在线式增长的特点，对这样级别数据量的音乐样本进行类别标注，无论是在人力上还是在时间成本上，都是不现实的。因此寻找更高效率的svM增量学习算法，筛选可以涵盖大量未标注样本所含信息量的代表性样本进行标注来改善分类模型的训练速度和分类精度，具有十分重要的意义。

从提高增量学习训练速度的角度出发，sved等基于SVM提出一种简单增量学习算法，该算法使用能够代表初始样本集但数量较小的支持向量进行训练。然而，该算法完全忽略了非支持向量，而有些非支持向量可能携带着由于训练前期样本不够丰富而没有显性表现出来的重要分类信息。申晓勇等通过分析训练样本的特点，结合KKT条件，提出一种计数器淘汰算法，有效地去除了少量无用样本，但该算法在增量学习的过程中需要对所有的历史训练样本进行学习，这将在很大程度上增加存储空间成本，同时也会使得增量学习的速度减慢。文献使用训练样本到类样本中心点的距离和该样本到分类决策平面的距离的比值，无异于改善分类模型性能的样本剔除，但算法存在一定的主观性，分类模型的稳定性无法得到保证。

研究发现，不同类别的训练样本在空间中呈现聚类分布，并且类样本集的边缘样本相比支持向量，包含更多的分类信息，这类样本被称之为壳向量。文献基于样本的几何分布特点，使用训练样本集中的壳向量和类与类之间边界上的壳向量作为初始训练样本集参与训练。文献提出一种基于壳向量的增量式快速增量学习算法，该算法使得求解二次优化问题的计算量大大减少，提高了增量学习的收敛速度。但利用该算法只适用于线性空间中的两分类问题，不适合在现实中推广使用。

本文算法在总结分析前人学习算法的基础上，提出一種改进的SVM增量学习算法，将KKT条件和壳向量相结合，分别从新增样本集和初始训练样本集的角度，降低学习过程中的存储空间占有量，提高用于模型训练的样本集的丰富性和可靠性，从而改善分类模型的收敛速度和分类性能。

2.SVM相关理论

SVM是在严谨的统计学习理论的基础上发展起来的一种用于解决分类问题的机器学习算法，该算法将结构风险最小化原则和统计学习当中的VC维理论相结合，采用核函数映射的方式实现非线性的SVM，通过寻找使得分类间隔最大化的最优超平面，实现对不同类别样本的分类，在解决小样本、非线性以及高维模式识别等问题中效果显著。相比传统的分类学习方法有着更好的学习性能和泛化能力，被广泛应用于文本分类、目标识别和时间序列预测等领域U5471。

对于线性二分类问题，假设给定类别标签的训练样本集为（X₁，y₁），（x₂，y₂），…（x_n，y_n），x_i∈R^d，y_i∈{+1，-1}。其中，n为训练样本集的总数，d样本特征的维度，y样本的类别标号。寻找最优超平面可以归纳为求解平面f（x）=wx+b的最优解，使得该平面能够正确地将两类已知样本分离开，同时要求如图1所示的分类间隔Margin最大化。

定理2若新增样本中存在某些违反KKT条件的样本，则这些违反KKT条件的样本中肯定存在新的支持向量；若新增样本中不存在违反KKT条件的样本，则新增样本中肯定不存在新的支持向量。

定理3若新增样本中存在违反KKT条件的样本，则上次训练结果中的非支持向量有可能转化为支持向量。

根据上述定理可知，y_if（xi）<1是新增样本（x_i，y_i）违背KKT条件的充要条件。若新增样本满足原分类器对应的KKT条件，那么该新增样本的加入对原支持向量集不会产生影响，也不会改善原分类器的性能，可舍弃该样本。反之，如果新增样本不满足当前分类器对应的KKT条件，那么该新增样本将使得原支持向量集发生变化，应当将其加入到下一轮的模型迭代中参与训练。通过这种方式，新一轮的迭代训练只需考虑不满足KKT条件的新增样本，从而大大减少对新增样本的学习时间，同时又不会影响新增样本集原本所包含的分类信息。

3.2利用壳向量代替支持向量

根据支持向量机的原理可知，在训練分类器的过程中，所利用的是对分类器的性能起决定性的支持向量。而在SVM增量学习的过程中，支持向量会随着新增样本的加入发生变化。

原支持向量可能转变为非支持向量，原非支持向量也可能转变为有助于改善分类器性能的支持向量。而传统的SVM增量学习算法，仅仅利用了支持向量，对于可能包含重要分类信息的非支持向量则完全舍弃，这将在很大程度上影响分类器的训练收敛速度和分类准确率。因此，在增量学习的过程中，新一轮的迭代训练样本集应该将历史训练样本集中的非支持向量考虑在内。

根据对训练样本集几何分布特征的分析，发现最有可能转变为支持向量的样本是类样本的边界附近的样本，即每个类对应的样本集中位于几何边缘的样本。这种特征的样本，就是本文算法所用到的壳向量。它不仅保留了原来的支持向量，而且还包括了最可能转变为支持向量的非支持向量，这使得原本被舍弃的可能包含重要分类信息的样本得以保留。获取壳向量的方法如下：首先求出训练样本集中各类别样本对应的最小超求体，然后以超球面上的点作为初始的壳向量，通过迭代方法求出其极点集合，最后从所得集合中舍弃多余的内点，从而得到训练样本集所对应的壳向量。

3.3算法描述

在传统的SVM增量学习算法中，每一轮的迭代训练只考虑支持向量，而对于可能转变为新的支持向量的非支持向量采取了全盘丢弃的措施，所训练得到的分类器的泛化性能较差。同时，该算法对于新增样本的选择策略是将其全部加入到原训练集，这将大大增加分类器训练的时间成本。基于上述不足之处，本文综合考虑原训练样本集和新增样本集的特点，使用包含更多样本分类信息的壳向量代替支持向量，它不仅包含了原来的支持向量集，而且保留了最有可能转变为新的支持向量的非支持向量。同时，根据样本是否违背KKT条件，从新增样本集中筛选出包含更多分类信息量的样本，以此减少模型训练时间。该算法使得训练得到的分类器在性能和训练时间上都能得到较好的优化。具体算法如下：

（1）设初始训练样本集为Traino，对应的初始壳向量为Hullo，第k次增量样本集为Addk，第k次增量学习中违背KKT条件的增量样本集为Add_k-violateo其中，k=l，2…n，n为加入增量样本的最大次数。

（2）利用上述求解壳向量的方法，求解初始训练样本集Traino中各类样本对应的壳向量并求并集，得到Traino的壳向量Hullo。

（3）将壳向量Hullo作为新的训练样本集，使用标准SVM算法训练得到分类模型Modelo。

加入新增样本集Addk，如果k>，2，则算法终止；否则转

（3）。

（4）根据分类模型Modelk-1，从Addk中选择违背KKT条件的增量样本，确定参与第k次增量学习的新增样本集Addk violate。

（5）如果Add_k-violateo=φ，置HUllk=HUllk-1，Modelk=Modelk-1，k=-k+l，转（3）；否则转（6）。

（6）对壳向量Hullk=Hullk-1UAddk_k-violateo进行增量学习，得到新的分类模型Modelk，并置k=-k+l，转（3）。

4.实验结果与分析

为了验证本文算法的可行性和有效性，本节分别从收敛速度和分类准确率两个角度，将本文提出的改进的增量学习算法与经典的SVM增量学习算法进行对比分析。实验所用的数据集为UCI数据库中的Balance Scale数据集和人工采集的音乐样本数据集。

Balance scale数据集：共有625个样本，样本特征维数为4，样本类别数为3，训练样本数为470，测试样本数为155。

人工采集的音乐样本数据集：共有3 301个样本，样本特征维数为100，样本类别数为5，训练样本数为2 500，测试样本数为801。

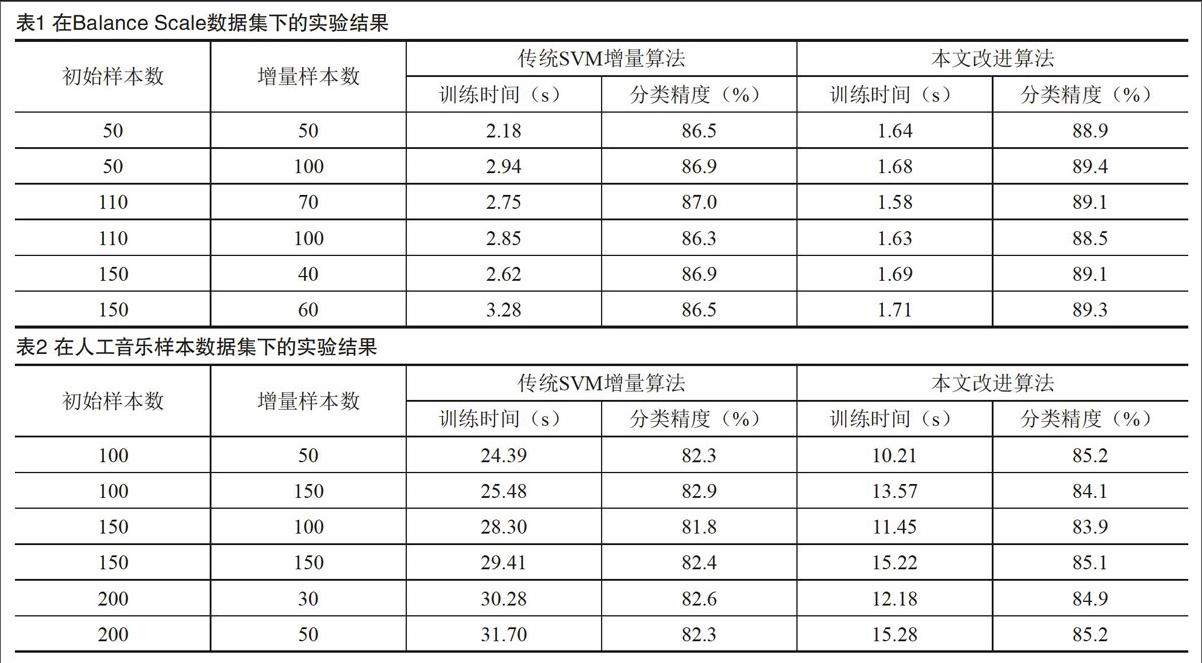
实验采用的分类环境为SVMlight，并根据实验数据的特点，选用径向基核函数。实验所需的初始训练样本集通过聚类算法生成。为排除单次实验结果的偶然性，实验将10次同样条件下的运行结果取平均值作为该条件下的实验结果。两个数据集的实验结果如表1-2所示。

由表1-2所示的实验结果可知，与经典的SVM增量学习算法相比，本文算法的分类精度明显高于前者，该结果表明，相比之前的支持向量，壳向量包含了更多有用的分类信息。同时，本文算法的训练时间相比前者缩短了接近一半。这也说明，选择违背KKT条件的新增样本参与训练的方法是可行的，不仅缩短了训练时间，而且无用样本的剔除也进一步改善了模型的分类性能。以上结果验证了本文算法的可行性和有效性。

5.结语

本文基于支持向量机的特性和前人的研究成果，提出一种改进的增量学习算法。该算法综合考虑历史训练样本和新增训练样本的特点，使用壳向量代替支持向量，以此来保留更多的历史分类信息。同时利用KKT条件对新增的训练样本集进行约简，只保留最有可能转变为支持向量的样本参与新一轮的增量训练。实验结果表明，相比经典的SVM增量学习算法，该算法具备较短的训练时间和较高的分类精度，并且能够保证良好的推广效果。