运用信息论的简单方法求解玻尔兹曼熵

吕桦

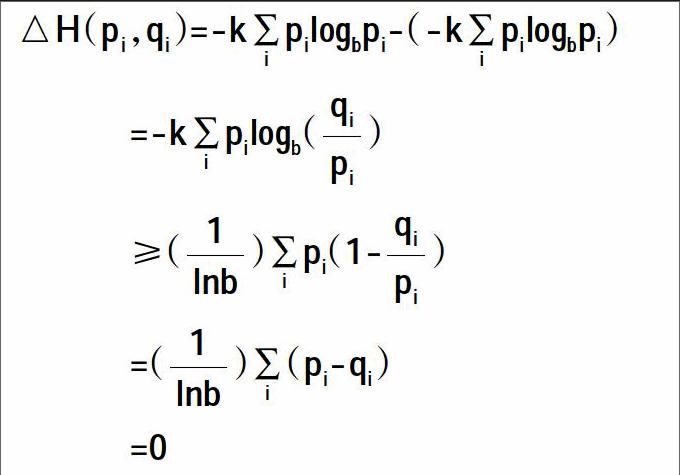
摘要：我们运用信息论提出了一个简单的方法求解了玻尔兹曼熵。首先，我们从定理中得到熵的一般公式：两个独立的事件所获得的信息与两个事件单独获得的信息是相同的。系统中所有的事件等概率发生时熵达到最大值，然而熵的一般公式就变为一个特例，即玻耳兹曼熵。我们用统计力学中的信息理论可以获得玻尔兹曼熵。

关键词：玻尔兹曼熵；信息理论；统计力学

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2017）15-0211-02

一、引言

熵的概念最早是由Clausius结合热力学第二定律提出的，且用它描述一个热力学系统的状态改变或者状态变化过程中的化学机制。随后，玻尔兹曼赋予熵一个统计模拟的定义来测量理想气体的无序和混乱程度[1]，他发现系统熵的值与它微观状态数的对数是成正比的。之后，Shannon把熵的概念应用到信息理论中用来衡量在传送信息过程中的信息量[2-5]。1957年，Jaynes把信息理論和统计力学统一了起来[6-9]。他认为当统计力学只是一种统计推理而不是物理理论的时候，统计力学中的一些基本计算法可以变为最大熵的定理。在Shannon熵理论中使用拉格朗日乘子法能估算出其最大熵值。当温度、自由能等参量的值被求出后，若不计玻尔兹曼常量，具有概率分布信息熵的热力学熵也可以被确定。特别地，当只有统计系统的平均能信息时，最大熵概率分布将成为玻尔兹曼分布。在这篇文章中，我们运用信息论提出了一个简单的方法可以得到玻尔兹曼熵S=kBlnW。我们运用简单的原理得出熵的一般公式，再通过简单的计算求出最大熵的一个分布，最后用概率论和微观的关系求出玻尔兹曼熵。这为学生学习热力学和统计力学课程中的玻尔兹曼熵提供了另一种方法。更近一步的说，我们从信息论中得出的玻尔兹曼熵仍然有助于研究生和本科生去理解熵和信息之间的关系。

二、信息熵的一般公式

在统计力学中，熵描述物理系统的无序或者混乱程度。它可以描述一个物理系统或一个事件的不确定性。这里，如果变量X的值是不确定的，我们通过一个测量得到有关变量X的信息量I（X）。这些信息将成为概率P的函数，它标示着变量X的概率分布。为了获得I（X）的形式，我们应考虑测量后信息获得后的特点。这里有一个简单的定理：从两个独立的事件中获得的总信息等于从两个事件单独获得信息的总和，即I（p，p）=I（p）+I（p）。很显然，对数函数满足这个公式。因此，可以用公式I（p）=-klogp来表示信息的增加，其中，b为对数函数的底数。我们取常用对数、二元对数、自然对数的底数分别为10、2和e=2.718。为了方便计算，我们假设底数b?1，k为常数，p∈[0，1]，这里加负号用来确保信息增加量是非负的。由于事件发生的不确定性，我们取信息增加量的平均值，用p，p，…，p表示，即（p，p，…，p）=-k∑plogp，接下来，我们定义两个具体事件信息增加量的取值范围，这里取P为0或1，如果事件从不发生取值为0，相反，如果事件在每次测量时都发生，即为全概率确定事件，信息的增加取值仍为0。举一个例子，在一个“是”或“否”的硬币游戏中，如果一个硬币总是正面朝上，人们就不会从结果中再获得任何有用的信息。因此，我们定义当P=0或1时，I（P）取值为I（0）=I（1）=0。平均信息增加量的一般公式可以写作为I（X）=I（p，p，…，p）= -k∑plogp （1）其中，∑p=1，0log0=0。

三、信息熵中求玻尔兹曼熵

信息具有物理性，信息的输入、存储、转换和输出都必须依赖于物理系统。在一个完整的测量结束后，测量者能获得系统的信息、不确定度以及系统熵的减少量。因此，公式（1）中的I（X）仍然可以被用来测量物理系统的不确定度，即H（X）=H（p）≡H（p，p，…，p）=-k∑plogp∑p，如果这里常量k取值1，熵的一般公式为众所周知的Shannon熵。下面我们将介绍如何从公式（1）的一般熵求得玻尔兹曼熵。

若给出热力学系统的一个宏观状态粒子，我们是无法获知它具体存在的位置。假设系统的一个宏观状态包含n个可能的微观态，那么系统第i个微观态的概率为p，则系统熵的不确定量为H（p）=-k∑plogp。下面我们确定系统熵的最大值。因为熵是系统不确定度的量度，所以我们可以直观的认为系统处于完全无序状态，即所有微观态等概率发生时，熵达到最大值。为了证明这个观点，我们测量两个概率分布相近的微观态，即p和q，这里采用相同的下标，i表示系统第i个微观态。这两个概率分布熵的距离可以写为[10]：

在上面的不等式中，我们运用了 两个公式，不等式当且仅当x=1时取等号。很显然，它意味着若两个事件概率分布不相同时，那么两个概率分布的距离是非零的，这里我们用相同的下标i标注。现在我们使用上面的不等式证明当处于完全无序状态时系统达到熵的最大值。令 得到

从上面的不等式可以得出klogn≥H（p）。当且仅当微观状态等可能发生时即p=时等式成立。很显然，我们得到具有n个可能微观态系统熵的最大值为 klogn。当k取玻尔兹曼常量kB、b取值e（即这里使用自然对数函数）时，系统的最大熵值还原为标准玻尔兹曼熵，S=klnW （2），这里W=n，代表微观状态数。到此，采用上面的方法我们证明了当所有微观态等概率发生时，物理系统的熵可以达到最大值，其值为玻尔兹曼熵。

四、讨论和结论

对信息熵和玻尔兹曼熵之间的关系的讨论已经有很长时间了。文中我们提出了一个更简单的方法从物理系统的信息熵中获得玻尔兹曼熵。我们的推导过程基于简单的基本原理即两个独立的事件所获得的信息与两个事件单独获得的信息总和是相同的，得出当系统处于热平衡状态时，即系统所包含的微观态等可能发生时，系统的信息熵达到最大值，即为玻尔兹曼熵。这里，如果系统的温度给定，系统玻尔兹曼熵中的玻尔兹曼因子[11]也能被确定。根据玻尔兹曼因子，系统的某些热力学特性也可以被进一步的研究。我们求解玻尔兹曼熵的过程暗示着未来统计力学很有可能被信息理论所建立。

致謝：感谢国家自然科学基金会（NSFC）的全力支持，批号为（11204072）。

参考文献：

[1]L. Boltzmann，Lectures on Gas Theory （English Translation），（University of California，Berkeley），1964.

[2]C. E. Shannon，A mathematical theory of communication. Bell System Tech. J.，1948，（27）：379-423，623-656.

[3]Qiao-Yan Wen，Fei Gao，and Fu-Chen Zhu，Quantum secure direct communication with χ-type entangled states，Phys. Rev. A，2008，（78）：064304.

[4]Bassano Vacchini，Klaus Hornberger，Quantum linear Boltzmann equation，Physics Reports，2009，（478）：71-120.

[5]R.A. Brownlee，A.N. Gorban，J. Levesley，Nonequilibrium entropy limiters in lattice Boltzmann methods，Physica A，2008，（ 387）：385–406.

[6]J?rg Reichardt and Stefan Bornholdt，Statistical mechanics of community detection，Phys. Rev. E，2006，（74）：016110.

[7]Alessandro Campaa，Thierry Dauxois，Stefano Ruffo，Statistical mechanics and dynamics of solvable models with long-range interactions，Physics Reports，2009，（480）：57-159.

[8]Hugo Touchette，The large deviation approach to statistical mechanics，Physics Reports，2009，（480）：1-69.

[9]E. T. Jaynes，Information Theory and Statistical Mechanics，Phys. Rev.，1957，（480）：620-630.

[10]S. Kullback，R. A. Leibler，On information and sufficiency，Annals of Mathematical Statistics，1951，（22）：79-86.

[11]H. B. Callen，Thermodynamics and an Introduction to Thermostatistics 2nd edn New York：Wiley and Sons，1985 chapter 15.