一种改进的无导数共轭梯度法

张一梦，贺祖国

（1.北京邮电大学理学院，北京 100876；2.北京邮电大学，北京 100876）

一种改进的无导数共轭梯度法

张一梦1，贺祖国2

（1.北京邮电大学理学院，北京 100876；2.北京邮电大学，北京 100876）

本文基于共轭梯度法的子空间研究，针对无约束优化问题提出了一种改进的无导数共轭梯度法。新算法不仅能有效弥补经典共轭梯度法要求线搜索为精确搜索的局限性，而且可适用于导数信息不易求得甚至完全不可得的问题。实验结果表明：相比于一次多项式插值法、有限差商共轭梯度法以及有限差商拟牛顿法，新算法的效率有很大的提高。

无约束最优化；无导数优化；子空间；共轭梯度法

0 引言

考虑无约束极小化问题

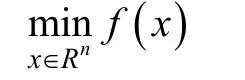
其中f:Rn→R二次连续可微。

目标函数的导数信息（梯度和 Hessian矩阵）在优化过程有着非常重要的作用。例如，对一个目标函数连续可微的无约束优化问题来说，由一阶最优性条件确定的稳定点处，其梯度为零。导数信息不仅能提供简单有效的停止准则，并且能有效的指引对试探点的选取。然而，很多来源于实际应用的优化问题的导数信息不易求得甚至完全无法得到，因此解决这类问题需要用无导数优化方法，也称为直接方法。

早期的无导数方法例如单纯形法，简单直观并且易于实现。发展到现在，无导数优化方法有直接搜索法[1-3]，线搜索法[4-6]，随机性算法，有限差商共轭梯度法和拟牛顿法[7]，基于差值模型逼近的信赖域方法等。

本文基于共轭梯度法的子空间研究[8]，将其运用于多项式插值算法中得到一种改进的无导数共轭梯度法。新算法不使用导数，实验结果表明，新算法提高了效率，是有效可行的。

1 共轭梯度法的子空间研究

共轭梯度法[9-12]是求解非线性无约束极小化问题[13]的一种经典算法，其基本思想是将最速下降方向与共轭性相结合构造一组共轭方向，在已知点处沿着这组共轭方向进行精确线搜索，求出目标函数的极小值和极小点。标准的共轭梯度法具有如下迭代形式：

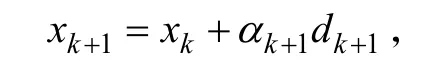
其中dk+1迭代形式如下：

根据以上形式可知，由于不同的kβ将会产生不同的搜索方向dk，因而得到的共轭梯度算法也不一样。

共轭梯度法的子空间研究，弥补了经典共轭梯度法要求线搜索为精确搜索的局限性。当线搜索为非精确搜索时，可在由 gk+1和dk张成的子空间span｛gk+1,dk｝中求dk。下面我们给出dk+1的迭代形式：

当gk+1和dk线性相关时：

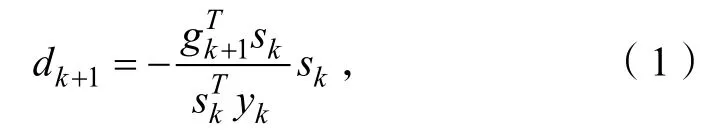
当gk+1和dk线性无关时：

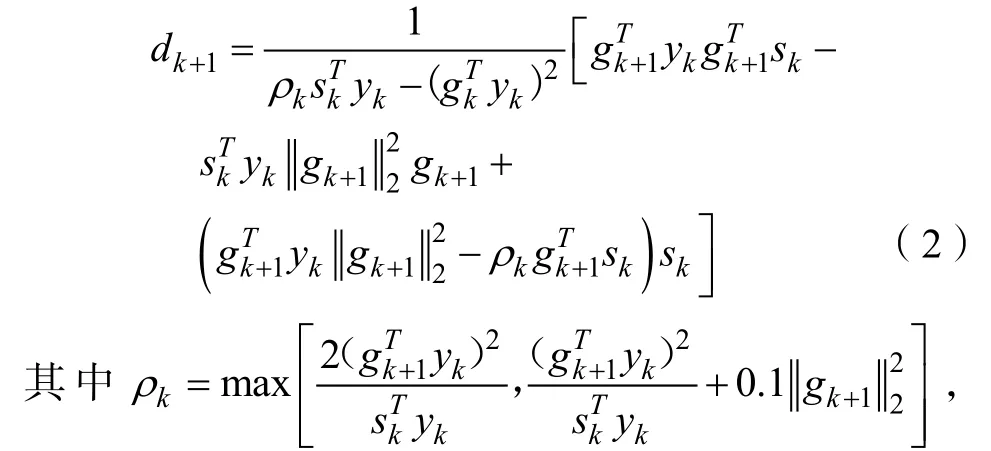
2 改进的无导数共轭梯度法

多项式插值法[13-16]属于无导数优化方法，其主要思想是用插值方法来构造目标函数的多项式逼近模型，计算过程中使用差商来近似梯度，不需要目标函数的导数信息。本文使用一次多项式插值模型来近似目标函数。本文将差商记为dg，设当前迭代点为xk，则此点处的梯度可由差商来近似，其中：

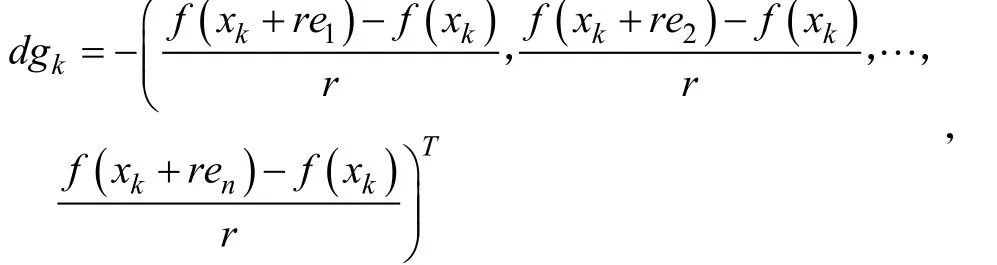
其中r为半径，ei∈Rn表示除第i个分量等于1外，其余分量均等于0的向量。

2.1 算法改进思路

本文的改进思路是将对共轭梯度法的子空间研究运用于多项式插值算法中，得到改进的无导数共轭梯度法。具体实现过程为：公式（1）和公式（2）求解搜索方向 dk+1时，用差商来近似梯度，然后沿此搜索方向进行搜索，求得目标函数的极小值点。

2.1.1 半径r的选择

关于半径r的选取，本文令初始半径r0=1。在之后的迭代时，若当前迭代点函数值与上一个迭代点函数值的距离小于α时，选取半径为当前迭代点函数值与上一个迭代点函数值距离的α倍，即。根据大量的数值实验，得出当α=0.01时实验结果较好，故本文中选取α=0.01。

2.2 算法步骤

基于上述改进算法的思想，改进后的算法步骤如下：

Step1：给定初始点 x0∈Rn，允许误差ε＞0，初始搜索方向d0=-dg0，k=0；

Step2：检验是否满足收敛性的判别准则：若dk＜ε，则停止迭代，点x*=xk即为极值点；否则进行Step3；

Step3：从当前迭代点xk出发，沿dk进行一维搜索，求kα ，使其满足，其中，一维搜索使用wolfe-Powell非精确线搜索，进行Step4；

Step4：令xk+1=xk+αkdk，计算gk+1=dgk+1，进行Step5；

Step5：构造搜索方向dgk+1：

3 数值试验

此次数值实验，所用电脑系统为Windows 10，内存为4.00 GB，处理器主频为2.30 GHz，编程环境为Mathematics10.1[17]。用Mathematic语言分别编写了一次多项式插值法、有限差商共轭梯度法、有限差商拟牛顿法和改进的无导数共轭梯度法的算法程序。在程序中，线搜索步长的选取均采用 Wolfe-Powell非精确线条件来进行，终止条件为dk＜10-8。

3.1 选用的测试函数

本文选取两个可变维数的测试函数：

3.2 数值结果

我们将一次多项式插值法记为算法 1，有限差商共轭梯度法记为算法 2，有限差商拟牛顿法记为算法3，改进的无导数共轭梯度法记为算法4。

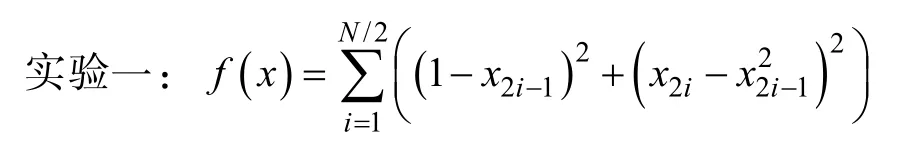
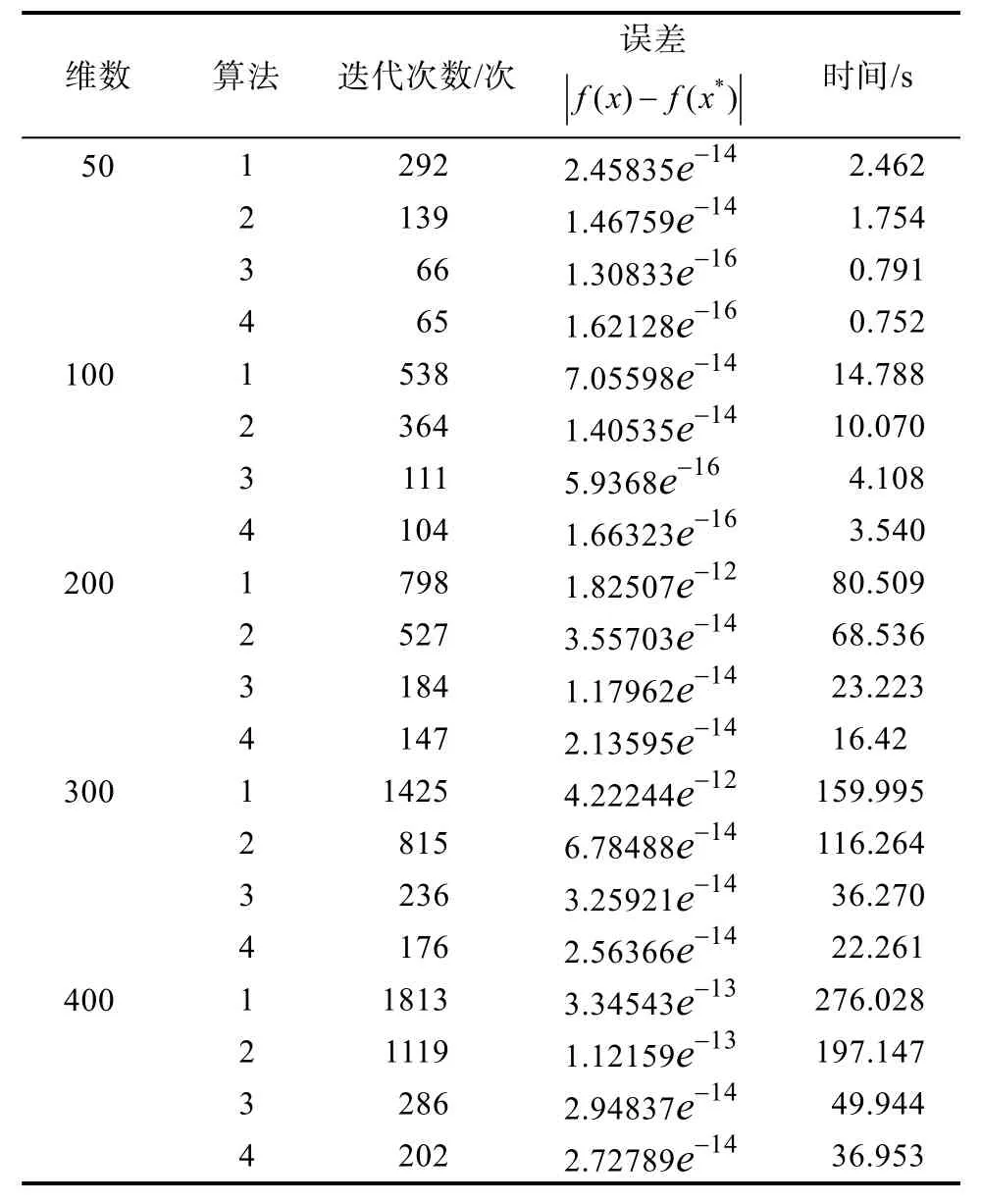
表1 Wolfe-Powell准则下四种算法的运行结果Tab.1 The results for the four algorithms at Wolfe-Powell

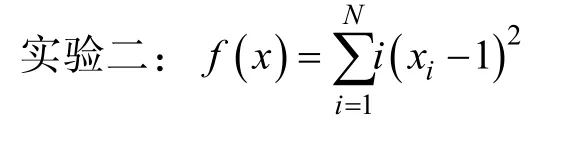
根据表1和表2中结果分析可得：不管是对于一些次数较高的函数，还是对于维数较大的函数而言，相比一次多项式插值法、有限差商共轭梯度法和有限差商拟牛顿法，改进的无导数共轭梯度法不仅迭代次数少，运行时间短，并且能收敛到很高的精度，具有良好的计算效能。

4 结论

大多数优化方法都依赖问题的导数信息，但在实际应用中，大量问题的导数信息都不可用，本文改进的算法可以很好的解决导数信息不易求得的无约束优化问题。在数值实验中，通过四种算法从迭代次数，运行时间，误差等方面的对比，数值结果也表明本文改进的算法是一种有效可行的方法。

[1]R.Hooke and T.A.Jeeves, Direct search solution of numerical and statistical problems, Journal of the Association forComputing Machinery, 8(1961), pp.212–229.

[2]E.Fermi and N.Metropolis, Tech.Report, Los Alamos Unclassifled Report LA–1492, Lo s Alamo s Na tional Laboratory, Los Alamos, NM, 1952.

[3]J.A.Nelder and R.Mead, A simplex method for function minimization, The Computer Journal, 7(1965), pp.308–313.

[4]H.H.Rosenbrock, An automatic method for flnding the greatest or least value of a function, Comput.J., 3(1960), pp.175–184.

[5]M.J.D.Powell, An e–cient method for flnding the minimum of a function of several variables without calculating derivatives, Comput.J., 7(1964), pp.155–162.

[6]W.H.Swann, Report on the development of a new direct search method of optimization, Tech.Rep.Research Note 64/3, I.C.I.Central Instrument Lab, 1964.

[7]G.W.Stewart, A modiflcation of Davidon’s minimization method to accept difierence approximations of derivatives, Journal of the ACM, 14(1967), pp.72–83.

[8]Yuan Y X, Stoer J.A Subspace Study on Conjugate Gradient Algorithms[J].Zamm Journal of Applied Mathematics & Mechanics Zeitschrift Für Angewandte Mathematik Und Mechanik, 1995, 75(1): 69-77.

[9]袁亚湘, 孙文瑜.最优化理论与算法[M].北京: 科学出版社, 1997: 1-330.YUAN Y, SUN W.Optimization Theory and Algorithm[M].Beijing: Science Press, 1991.1-330.(in Chinese)

[10]陈宝林.最优化理论与算法[M].北京: 清华大学出版社, 2005.1-358.CHEN B, Optimization Theory and Algorithm[M].Beijing: Tsinghua University Press, 2005.1-358.(in Chinese)

[11]M.J.D.Powell, Nonconvex minimization calculations and the conjugate gradient method, in: Lecture Notes in Mathematics vol 1066, Berlin: Springer-Verlag, 1984.122-141.

[12]戴彧虹, 袁亚湘.非线性共轭梯度法[M].北京: 科学出版社, 1982.DAI Y H, YUAN Y X.Nonlinear conjugate gradient method[M].Beijing: Science Press, 1982.(in Chinese)

[13]M.J.D.Powell, Direct search algorithms for optimization calculations, Acta Numerica, pages 288-336, Cambridge University Press, Cambridge, 1998.

[14]M.J.D.Powell, UOBYQA: unconstrained optimization by quadratic approximation, Report No.DAMTP 2000/NA14, University of Cambridge.

[15]M.J.D.Powell, On the Lagrange functions of quadratic models that are defined by interpolation, Opim.Methods Software, 2001(16), 289-309.

[16]M.J.D.Powell, Least Frobenius norm updating of quadratic models that satisfy interpolation conditions, Report No.DAMTP 2002/NA08, University of Cambridge.李汉龙, 缪淑贤, 韩婷.Mathematica基础及其在数学建模中的应用[M].北京: 国防工业出版社, 2013.

[17]LI H L, MIU S X, HAN T.Mathematica basis and its application in Mathematical Modeling[M].Beijing: Naional Defense Industry Press, 2013.(in Chinese)

An Improved Conjugate Gradient Method without Derivatives

ZHANG Yi-meng1,2, HE Zu-guo1,2
(1.Beijing University of Posts and Telecommunications, College of Science, Beijing 100876, China; 2.Beijing University of Posts and Telecommunications , Beijing 100876, China)

Based on the study of subspace of conjugate gradient method, an improved conjugate gradient method without derivatives is proposed for unconstrained optimization problem.The new algorithm can not only make up for the classical conjugate gradient method, but also can be applied to the problem that the derivative information is not easy to obtain or even completely unavailable.The experimental results show that the efficiency of the new algorithm is greatly improved compared with the linear polynomial interpolation method, the finite difference conjugate gradient method and the finite difference quasi-Newton method.

Unconstrained optimization; Optimization without derivative; Subspace; Conjugate gradient method

O221.2

A

10.3969/j.issn.1003-6970.2017.03.019

张一梦(1992-)，女，研究生，主要研究方向为最优化算法；贺祖国，男，(1972-)，教授，主要研究方向为数学建模，最优化算法。

本文著录格式：张一梦，贺祖国.一种改进的无导数共轭梯度法[J].软件，2017，38（3）：93-96