低信噪比下高精度通信信号载频盲估计算法

张亚丰，王 翔，赵成林

(1.北京邮电大学 信息与通信工程学院，北京 100876；2.北京简易科技有限公司，北京 100088)

低信噪比下高精度通信信号载频盲估计算法

张亚丰1，王 翔2，赵成林1

(1.北京邮电大学 信息与通信工程学院，北京 100876；2.北京简易科技有限公司，北京 100088)

未知制式的通信信号的载频估计是台站监测与频谱管理中的一个重要问题，针对现有载频估计算法的估计精度和复杂度不能兼得的不足，在分析信号功率谱特性的基础上，结合线性调制信号的功率谱的对称性，在频谱重心法的基础上提出了以一种改进的估计算法，首先对信号的功率谱进行平滑和高斯拟合的预处理，然后通过迭代搜索的方法估计载频大小，该算法无需知道信号的制式以及其他信息即可实现载频的盲估计，仿真结果表明，在高斯信道环境下，该算法可以实现对载频的快速估计，并且其在低信噪比下的估计较为精确，在台站监测方面有着良好的应用前景。

载频估计；谱重心法；高斯拟合；迭代搜索

0 引言

缺乏先验知识的通信信号载波频率盲估计是台站以及频谱监测领域[1-2]的一个非常重要的部分，载波频率估计的精确度对监测或截获信号后续的调制方式识别以及解调有着很大的影响。为了监测合法台站的工作情况以及频点使用情况，并且需要适应恶劣信道状况，因此需要一种抗干扰比较强的高精度载频估计算法。目前针对载频估计方法已经有了很多研究，大致可以归为时域与频域两类。文献[3]根据数字调制信号在每个载波周期会两次经过零点的特性，统计了接收到的信号在一段时间内经过零点的次数来估计载频，该方法复杂度低，但是在低信噪比下的估计精确度迅速下降。文献[4]采用了一种相位差分法，在高信噪比下对相位调制信号的估计性能良好，但是对非相位调制信号估计性能受限，且由于是时域估计方法，对噪声比较敏感。文献[5]对信号进行了M倍频，频谱搬移到了M*fc处，然后搜索频谱最大值，就可以得到载频的估计值，该方法需要知道信号调制方式等先验知识，而且在倍频的时候，噪声也相应的被同样的处理，噪声影响被放大，估计结果精度降低。文献[6]针对时域算法对噪声的敏感性，提出了一种经典的载频估计方法，频率重心法，通过计算频谱的重心位置来估计信号载频，方法简单，但是在估计性能同样在低信噪比下受限。因为常用移动通信信号都具有循环平稳的特性，文献[7，8]提出了基于循环谱和循环累积量的载频估计算法，这两种方法可以抑制噪声，尤其高阶循环累积量理论上可以完全消除噪声，相对前几种方法估计精度有了很大提高，但是这两种方法运算复杂度也成倍的增加。

本文在研究了移动通信信号功率谱特性和文献中所提到的算法的特性，针对目前估计算法低复杂度与高准确性不可兼得的不足，在复杂度较低的频谱中心法基础上，提出了一种改进的低信噪比下低复杂度载频估计算法，该方法首先利用了直接法求取信号的功率谱，并对其平滑和进行高斯拟合得到平滑的功率谱曲线，然后利用功率谱对称性，对功率谱曲线左右快速上升和下降的区间进行求和逼近，进而求得载频估计值，最后针对2G、3G、4G移动通信信号的载频估计进行了MonteCarlo仿真实验。

1 信号模型的建立和功率谱估计

1.1 信号模型

此处三种制式的信号可以处理为一个接收信号模型，设接收到的信号有以下的形式：

其中，s(t)为经过载频调制后的移动通信信号，I (t)和Q(t)分别为基带调制信号的同相分量和正交分量，具体表达形式如式（3）与（4）所示，n(t)为零均值的高斯白噪声， fc为载波频率。

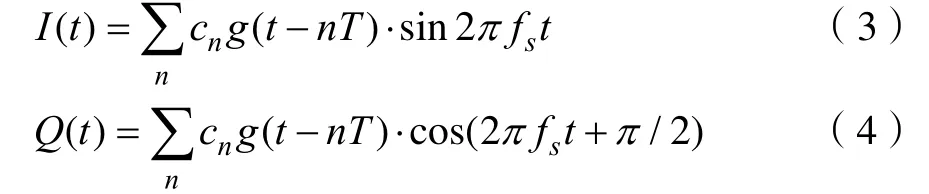
其中cn为发送符号，承载了需要传输的信息，T为符号周期，g(t)为脉冲成型。

1.2 功率谱估计

在实际的监测以及非协作通信系统中，接收到的通信信号是具有某种统计特性的随机信号，并且由于需要对信号进行快速的分析，因此，本文选用最简单的谱估计方法--周期图法，对该信号进行谱分析，功率谱Q(f)的表达式，如式（5）所示:

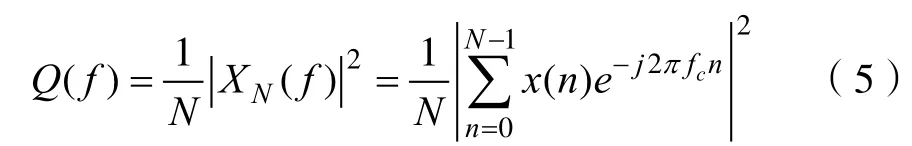
其中XN(f)为采样得到的信号x(n)的傅里叶变换，周期图法虽然是渐进无偏估计，但是因为相对其他平谱分析方法，周期图法的分辨率较高，因此得到的功率谱不平滑，且变化幅度较大。所以，针对周期图法的一些缺点，采用对谱线加窗进行中值平滑的方法来功率谱进行第一步处理，经过平滑后的功率谱线仍然会有很多毛刺，因此针对平滑后的功率谱线采用高斯曲线拟合对谱线进行第二步处理。

2 改进的载频盲估计算法

2.1 高斯非线性拟合[9]

经过平滑的功率谱细节处还是有很多毛刺，因此在此基础上对功率谱做一个简单的高斯多项式拟合会提升功率谱平滑效果，以便后续的处理。一般对数据进行拟合的方法是：对给定的仿真数据(xi,yi),(i=0,1,2,3,···,m),在选取的函数类φ中，通过若干次的迭代，求得 f(x)∈φ，使 f(x)与yi的误差平方和最小[10]，即

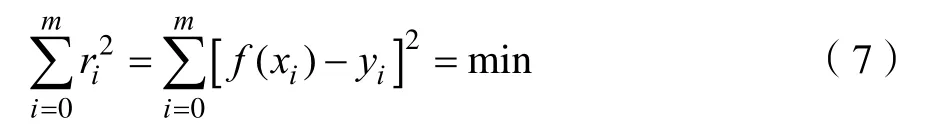
求得的 f(x)即为实际数据的拟合函数，求取f(x)的过程为曲线拟合。在曲线拟合中，可以选择不同的基函数进行拟合，本文选用高斯函数进行曲线拟合。

高斯拟合主要使用形如式（8）的函数对数据集进行拟合，高斯拟合和多项式拟合类似，也是运用最小二乘法进行逼近，不同的是函数不一样：

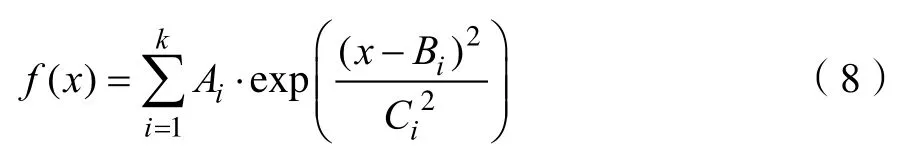
k为阶数， f(x)即为k个高斯函数的组合。

求取高斯函数的主要原理如下：

设现在有一组需要拟合的数据为(xi,yi)(i=0, 1,2,3,···,m)，可用式（9）高斯函数描述，即

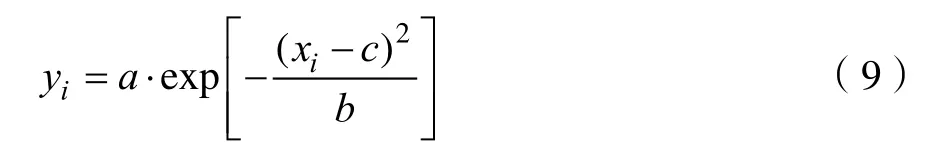
式（9）中需要估计的参数有三个，为a,b,c，分别代表的物理意义为高斯曲线的峰高、半宽度信息和峰位置，将（9）两边取自然对数得：

令

则式（10）化为二次多项式拟合函数

考虑全部数据和量测误差，用矩阵形式表示如下：

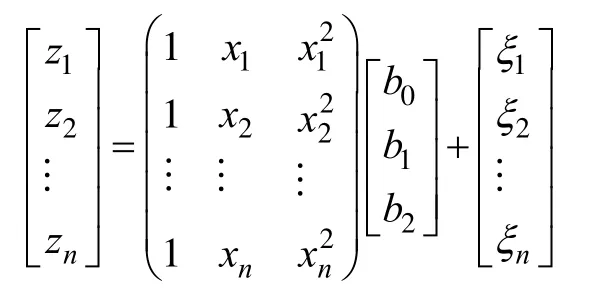
记为Z=XB，可求得矩阵B的广义最小二乘解为B=(XTX)-1XTZ ，由此可以求得参数a,b,c，进而求得（8），本文选用高斯基函数为4个。

2.2 算法原理

用WCDMA信号做事例分析，信号模型如第一节所示，码率为3.84 Mcps，图1是WCDMA信号未加噪声的功率谱梯度曲线，其他两种信号类似，从图中可以看出，功率谱上升和下降区间比较窄，即谱线上升或者下降比较迅速，因此受噪声影响比较小。

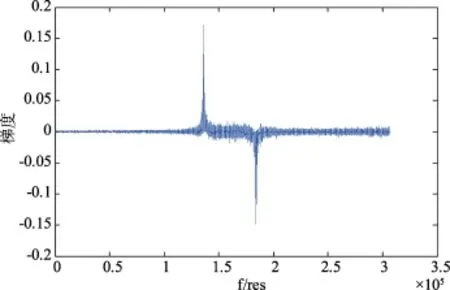
图1 功率谱梯度曲线

经过线性调制的信号的功率谱与信号载频有式（12）的关系，即功率谱上升段与下降段是关于载频对称的，因此利用功率谱对称性提出了在谱重心法估计载频的基础上的修正算法。

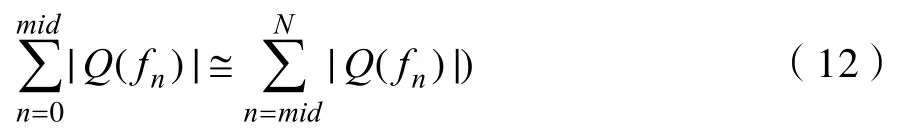
算法估计流程的详细描述如下：

Step1：先对信号进行求取功率谱，本文采取周期图法，由公式（1）对x(n)求取FFT，可以的到对应的频谱，然后根据公式（14）可以得到功率谱

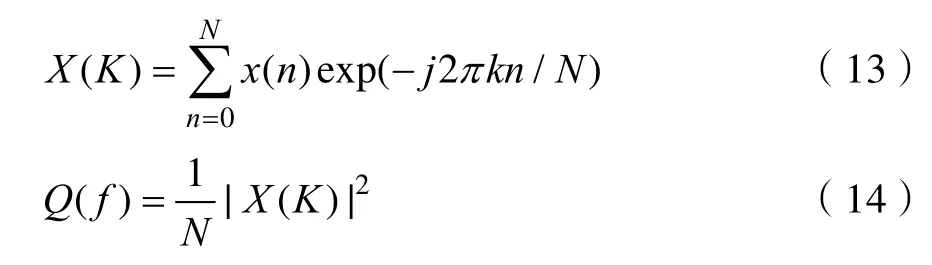
Step2：对功率谱进行平滑和高斯拟合，然后频谱中心法公式（3），可以得到 fd：

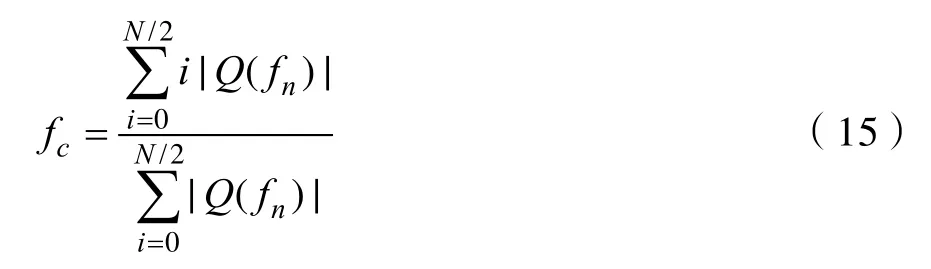
Step3：根据Step2中的 fd或者根据搜到的最大功率谱值Maxi，向两边搜索3dB带宽的大致位置，可以得到信号的3db带宽band=Band_3dB(Hz )

Step4：在 fd左右两侧选取相同长度大小的频带，即需要保证，fL1和 fL2以及 fR1和 fR2的确定，由上一步频率重心法得到的 fd以及下面的公式求取，公式如下：Step5：根据两频带区间的功率谱值之和进行算法迭代，迭代的逻辑控制伪代码如下：

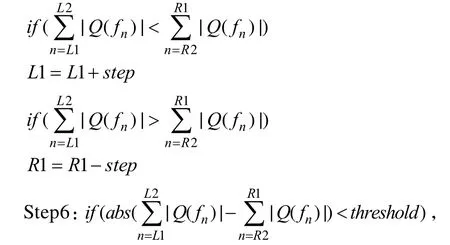
停止，否则继续进行step5，经过若干次迭代以后，可以得到载频的最终估计结果是

注：

1.在步骤 4中，c1取常数（试验中取 0.6），distanc是常量，在算法初始化以后，在迭代过程中保持不变。

2.上面在步骤 5中，step取值在5～10之间，取值越小越精确，取值越大迭代速度越快。

3.Threshold由如下公式确定

c根据实际情况取1～3之间的常数。

3 仿真结果结果与分析

3.1 仿真结果

本文分别对三种制式的移动通信信号在不同信噪比进行了仿真和分析，仿真结果主要包括两部分内容，第一部分主要论证了算法的收敛性；第二部分主要评估算法对信号载频的估计性能，其中采用了两中估计方案：1）没有经过优化的频谱重心法，2）本文提出的迭代算法。在不知道信号先验条件下，以及较低信噪比的情况下，可以明显看出，算法2）的估计性能比算法1）的性能更好。

3.1.1 算法的收敛性能的仿真

在不同信噪比下，分别对三种制式的通信信号进行100次蒙特卡洛仿真实验，得到的算法平均迭代次数的仿真图如图2所示。

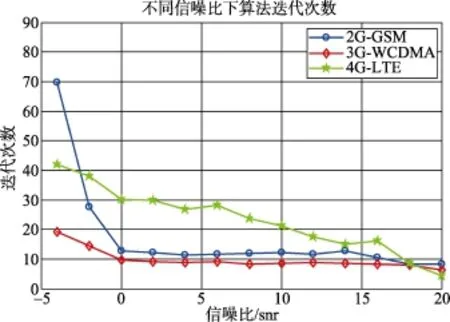
图2 不同信噪比下算法的迭代次数

从图2我们可以看出算法速度收敛非常快，并且随着信噪比的提升，算法的迭代次数在减少，因为在随着信噪比的升高，谱重心法的估计性能也在提升，因此文中所提在此基础上的迭代修正次数也会减少，运算量也会随之降低。

3.1.2 算法对信号载频的估计性能的仿真

这一小节主要对算法性能进行了仿真分析，因为是对通信信号的载频进行估计，因此选用GSM、WCDMA、LTE三种制式的信号，信号背景噪声为高斯白噪声，即信号传播信道为AWGN信道，对背景噪声大小的描述用SNR（信噪比）来进行描述，采用平均相对误差（式（21））来评价载频估计的精确度。

在不同信噪比下分别进行100次蒙特卡洛仿真实验，得到两种算法的估计平均相对误差曲线分别如图3、图4和图5所示：

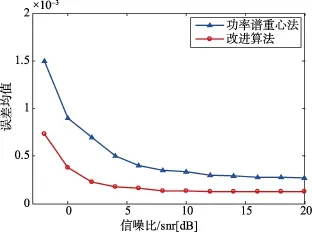
图3 GSM信号估计误差均值曲线

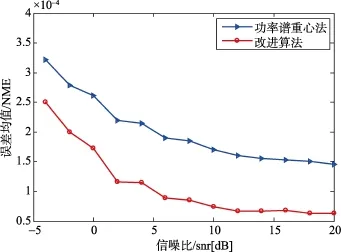
图4 WCDMA信号估计误差均值曲线

图5 LTE信号估计误差均值曲线

分析上面三幅图的结果可以看出，总体上，所提算法相对谱重心法的估计性能表现良好；随着信噪比的降低，频率重心法对信号载频的估计精确度下降较快，在0 dB到10 dB区间估计结果的精确度急剧下降，文中所提改进算法对载频估计精度提升明显，尤其当信噪比在0 dB以下的时候，所提算法的估计精确度仍然比较高，较原来算法估计精度有所提升，证明算法的抗噪性能良好。通过上面的实验仿真可以看出文中所提算法对通信信号的载频估计准确度较高而且非常有效。

4 结束与展望

本文根据信号监测系统的需要，针对三种制式的通信信号，提出了一种在缺乏先验知识的情况下，准确快速估计信号的载频的方法。利用平滑和高斯拟合对信号进行预处理，结合信号功率谱的对称性对载频估计结果进行迭代修正，使算法在低信噪比下也有良好的性能，能够满足监测系统在全盲状态下对信号载频估计的需要。在以后的研究中，还会对步长和门限动态调整进行研究，更好的适应信号监测系统。

[1]孙健, 张锦南.频谱资源利用评价体系研究[J].软件, 2016(2): 17-21.

[2]孙大飞, 宋铁成, 吴名, 等.频谱感知能量检测器的性能分析[J].新型工业化, 2012(10).

[3]Cai H.Fast Frequency Measurement Algorithm Based On Zero Crossing Method[C]// Computer Engineering and Technology (ICCET), 2010 2nd International Conference on.2010: V4-606-V4-608.

[4]Wei J.Modification of frequency estimation algorithms for sinusoidal signals based on phase difference of overlap FFT[C]// International Conference on Communications, Circuits and Systems.IEEE, 2008: 927-929.

[5]Hill D A, Bodie J B.Experimental carrier detection of BPSK and QPSK direct sequence spread spectrum signals[C]// Military Communications Conference, 1995.MILCOM '95, Conference Record, IEEE.1995: 362-367 vol.1.

[6]Hui L, Dai B Q, Wei L.A Pitch Detection Algorithm Based on AMDF and ACF[C]// IEEE International Conference on Acoustics.2006: I-I.

[7]黄春琳, 柳征, 姜文利, 等.基于循环谱包络的扩谱直序信号的码片时宽、载频、幅度估计[J].电子学报, 2002(09): 1353-1356.

[8]郑文秀, 赵国庆, 罗明.基于高阶循环累积量的OFDM子载波盲估计[J].电子与信息学报, 2008(02): 346-349.

[9]唐冲, 惠辉辉.基于Matlab的高斯曲线拟合求解[J].计算机与数字工程, 2013, 41(8): 1262-1263.

[10]刘明骞, 李兵兵, 王婧舒, 等.低信噪比下低复杂度的OFDM信号带宽盲估计方法[J].江苏大学学报(自然科学版), 2013, 34(01): 76-80.

High-Precision Carrier Frequency Blind Estimation Algorithm for Communication Signals with Low SNR

ZHANG Ya-feng1, WANG Xiang2, ZHAO Cheng-lin1
(1.Beijing University of Posts and Telecommunications, Department of Communication and Information System, Beijing 100876; 2.Beijing jianea technology Co., Ltd., Beijng 100088)

The carrier frequency estimation of the communication signal of unknown standard is an important problem in the station monitoring and spectrum management.Considering the shortcomings that existing carrier frequency estimation algorithms do not have both high accuracy and low complexity, so aiming at the symmetry of the power spectral of the linear modulated signals, an improved estimation algorithm based on the spectral center of gravity method is presented.First, the power spectrum of the signal is smoothed and pretreated by Gaussian curve fitting.Then, the carrier frequency can be estimated accurately by the proposesd method of iterative search.The algorithm can realize blind estimation of carrier frequency without knowing the signal format and other information.The simulation results indicate that the algorithm can realize fast estimation of carrier frequency in Gaussian channel environment, as well as more accurate in low SNR.In summary, it has a promising application prospect in the station monitoring.

Carrier frequency estimation; Frequency mediacy method; Gaussian fitting; Iterative search

TN911

A

10.3969/j.issn.1003-6970.2017.03.017

张亚丰(1993-)，男，硕士研究生，主要研究方向为无线信号处理，参数估计；王翔(1969-)，男，主要研究方向为频谱监测，网络通信。

赵成林(1964-)，男，教授，主要研究方向为无线信号处理与信号检测。

本文著录格式：张亚丰，王翔，赵成林.低信噪比下高精度通信信号载频盲估计算法[J].软件，2017，38（3）：82-86