计算机网络模型中的神经网络算法分析

王建国

摘要：随着我国社会不断进步，计算机网络也在迅速发展，在计算机网络迅速发展的过程中，需要全面提高计算机网络的整体性能，计算机网络模型算法具有分布式信息存储、规模性的并行信息处理特点，并且还具有优化和联想记忆的优势，基于计算机网络模型中的神经网络算法研究，是计算机网络和神经网络算法优化方式相结合的表现。

关键词：计算机网络模型；神经网络算法；分析

中图分类号：TP393 文献标识码：A 文章编号：1009-3044（2016）35-0212-02

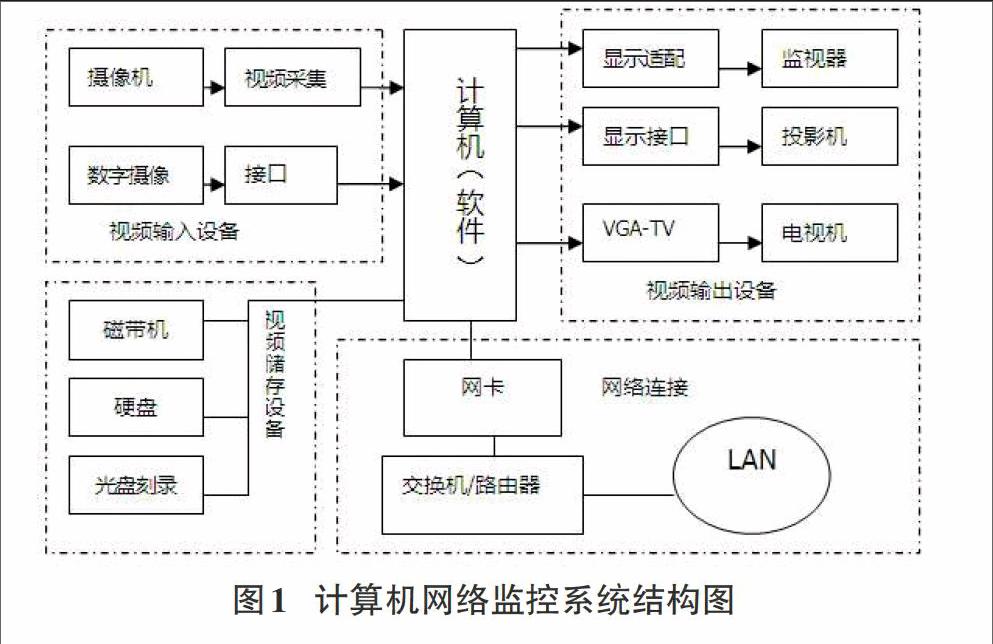
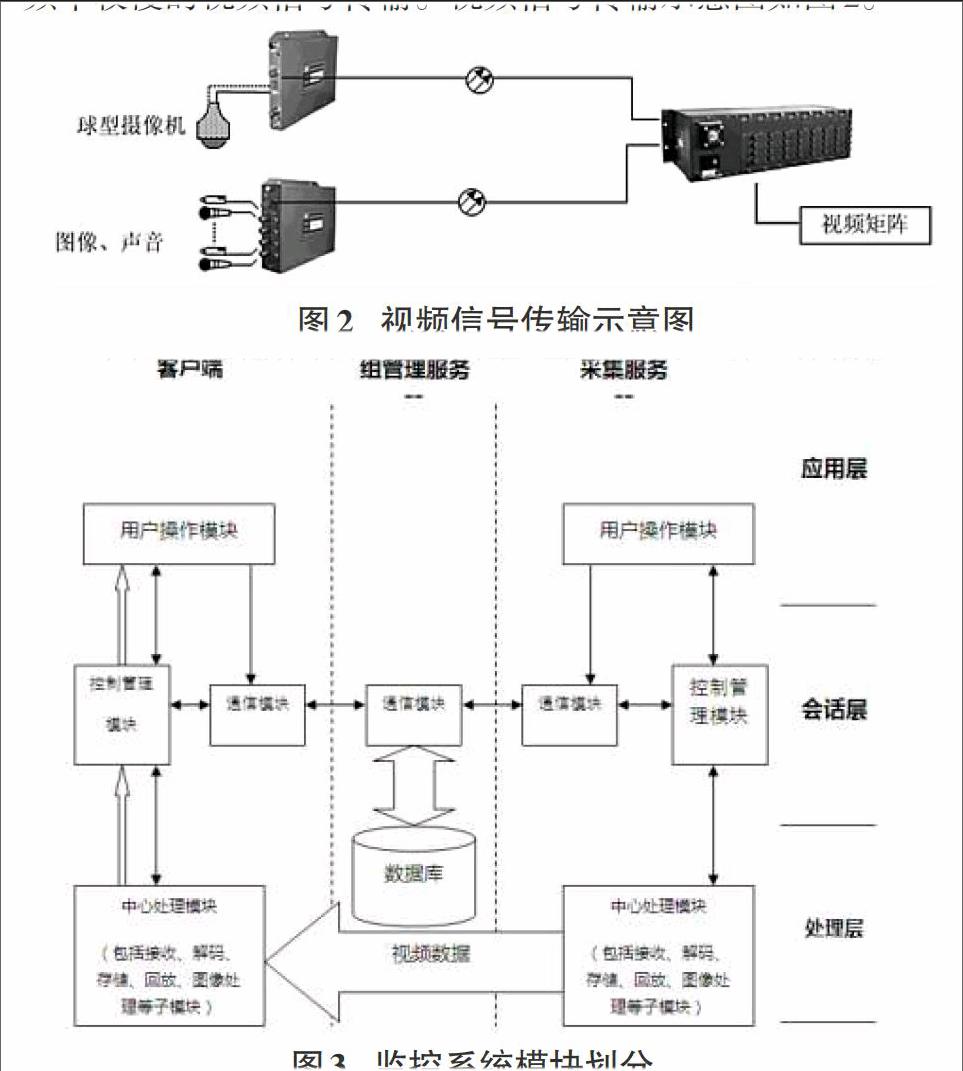
计算机网络是人们多年研究科技进步最重要的成果，其被广泛运用到教育、工作、科学等方面，也具有良好的成就。目前，基于服务器的集线式网络具有实现网络互连的功能，但也成为了网络进一步发展的阻碍。虽然大量的信息能够丰富网络中的内容，但是其中的多媒体技术发展却使网络运行力不从心，比如图像、声音等，全面优化计算机网络整体性能是其发展的必要途径。将神经网络算法与计算机网络相结合，能够有效解决大规模复杂性的问题。

1浅析神经网络算法

1.1神经网络算法内涵

思维界认为，人类大脑思维包括灵感思维、逻辑思维、形象思维三种方式，神经网络模拟的就是人类思维的形象思维，是一种非线性动力学系统。神经网络算法指的是逻辑性思维根据逻辑规则推理的过程。神经网络的内容目前被广泛研究，包括建立理论模型、生物原型研究、建立网络模型与算法研究、人工神经网络应用系统等。

优化网络的神经网络主要是Hopfield神经网络，是1982年由美国物理学家提出的，它能够模拟神经网络的记忆机理，是全连接的神经网络。Hopfield神经网络中的每个神经元都能够信号输出，还能够将信号通过其他神经元为自己反馈，那么其也称之为反馈性神经网络。

1.2神经网络优化的基础

Hopfield神经网络其实是一个分线性动力系统演变的过程，通过能量函数分析系统的稳定性，将能量函数看做需要优化的问题目标函数。将能量函数的初始状态转变为稳定点这一过程，就成为求解优化问题过程，这个过程也可以称为在计算机联想记忆基础上解决优化问题的过程。

1.3神经网络优化模型的算法

反馈网络的联想记忆和优化是相对的，通过优化计算得知W，其目的就是为了找出E的最小稳定状态；联想记忆的稳定状态是特定的，要通过一些过程才能够找到适合的W。这个过程中的关键就是将问题的目标函数通过二次型能量函数进行表达。如下式所述：

Hopfield神经网络比较常见的类型有DHNN（离散型）和CHNN（连续性）两种，他们的动态方程分別为：

DHNN（离散型）动态方程：ui=fi（v1，v2，...，vN）

Vi=g（ui），vi∈{0，1}，i=1，2，...，N

式子中的gi表示为阶跃函数，vi=g（ui）[（1， ui>0）（0， ui<0）]，式子中的N表示神经元的数量，ui表示第i个神经元的输入，vi表示第i个神经元的输出。

CHNN（连续性）动态方程：dui/dt=fi（v1，v2，...，vN）

Vi=gi（ui），i=1，2，...，N

式子中的gi表示为常用函数sigmoid，vi=gi（ui）=1/2[1+tanh（ui/u0）]，u0表示的为可控函数的斜率，当u0=0的时候，gi就为阶跃函数。【1】

1.4神经网络算法的优化步骤

其一，通过合适的问题将方法表述出来，使神经网络的输出和这一问题的解相互对应；

其二，创建有效的能量函数，要求问题的最优解能够对应最小值；

其三，使用有利条件和能量函数创建网络参数；

其四，创建对应的动态方程和神经网络；

其五，使用有效的初值，要求网络根据动态方程进行验算，直到收敛。

2基于神经网络算法的网络流优化模型

网络流优化模型的关键就是最小切割、图的划分和最大流问题，下面一一描述：

最小切割：最小切割是指寻找使隔集容量达到最小的切割。图的切割是指划分一个N—n1Un2，一个隔集为一组弧（i，j），i∈n1，j∈n2，隔集弧的权值总和为它的容量。使N=（W，T）是T=0的网络，要求能量最小为N图的最小切割。

图的划分：图的划分指的是将图划分为K个部分，要求每个部分中的节点数都相等。

最大流问题。要求有向图G（v，e）中的开始点为S，结束点为Z，边容量为Cij。如果每条边都有非负数fij，并且每条边为fij≤Cij且除了S和Z之外具有∑fij=∑fki。当S和Z有∑fsi=∑fiz=W的时候，W的最大值≤任何切割的容量。【2】

3基于神经网络算法的动态路由选择模型

通信网中的物理网络的连接一般是点到点，其可以用无向图G=（v，e）来表示，将交换节点表示为顶点，通路表示为边，每一边都有最大容量，为了能够满足网络中点和点能够相互通信，还鞥能够根据网络业务的量和用户呼叫为基础进行路由安排。现在一般使用的都是静态方式，能够提供给动态路由一些可能性，其的优化模型是：

如果网络图是G=（v，e），而且对网络中的边进行编号，路径经过的边表示为1，路径不经过的边表示为0，L*M神经元表示为L需要这多个路由，将备选的路由数量表示为M，如果通信网中具有N个节点，那么目标函数就是E=E1+E2+E3。【3】

4结束语

基于神经网络算法的优化网络模型有着简单、稳定、快速、规范的优势，其与其他算法相结合，能够较大程度的提高计算机网络模型的整体性能。但是Hopfield神经网络算法中的优化网络模型并不严格，它有着核心策略下降的缺点，那么在使用过程中会出现网络收敛的最优解呈局面状态、网络收敛解不可行、网络参数的不正当选择会导致偏差等，所以在今后就要深入研究计算机网络模型中的神经网络算法，使其更加完善。

参考文献：

[1]丁建立.基于神经网络算法的计算机网络优化模型研究[J].洛阳师范学院学报，2003， 22（2）：59-62.

[2]朱云.计算机网络连接增强优化中的神经网络算法[J].煤炭技术，2012，31（4）：16-16.

[3] 倪顾伟.基于神经网络的数字水印算法的研究与实现[D].南京理工大学，2012.