Bootstrap在商业银行资产负债评价中的运用
金明+寇莉+俞高


摘 要:Bootstrap方法是一种利用样本信息来估计总体的非参方法,聚类分析方法是将样本或变量进行归类评价的一种多元统计方法。基于bootstrap抽样法和系统聚类技术对我国部分商业银行的资产负债况进行分析,聚类结果将各个商业银行的资产负债情况分为3类。
关键词:bootstrap;聚类分析;商业银行;资产负债
中图分类号:F83 文献标识码:A doi:10.19311/j.cnki.1672-3198.2016.33.104
1 引言
自Efron首次提出Bootstrap以来,在众多统计学家贡献下,bootstrap统计方法得到了充分的发展,尤其是在计算机技术发达的今天,bootstrap变得更加容易实现。就bootstrap方法的基本原理,Efron、Tibshirani、DiCiccio等曾作详细的论述。国内学者对bootstrap的研究也取得一定的成绩,施锡铨在上世纪九十年代论述过独立同分布数据的bootstrap逼近方法。更多的国内学者是运用bootstrap方法做实证分析,如赵亮、程锦秀等把bootstrap运用到生物学研究上,孙佳美、段白鸽利用该方法做死亡模型检验的研究,刘勤、金丕焕推广了bootstrap法在医学统计上运用。
国内学者对商业银行的研究主要集中于银行的效率分析,如魏煜、张建华、姚树洁、朱南、郑录军等对此作有详细的论述,详见参考文献。另外一些学者重点研究了我国商业银行的信用风险的评估问题,沈沛龙、王春峰、唐国储等在这个方面作出贡献。后来的学者也在继续关注着这些领域。涉及商业银行收益研究的国内文献并不多见,张铁铸曾从银行贷款的多元化角度研究银行风险、收益与之的关系;于研、孙磊运用SFA方法探索银行收益结构与银行效率的相关性;蒲勇健、李绍芳考察研究了金融衍生品对商业银行收益的影响;王连则运用了非参数统计手段研究了信用卡的信用额度变化与银行收益的关系;黄陈曾将我国商业银行收益水平作国际比较并归纳出商业银行收益的四个层次。银行的收益水平是投资者关注的重要指标之一,而银行资产负债情况正能反映银行经营状况,所以继续对此进行深入研究有着重要的现实意义。本文,笔者尝试利用多元统计技术并借助bootstrap方法来剖析我国商业银行的资产负债,分析各银行经营收益。
2 银行资产负债评价方法
2.1 BOOTSTRAP
Bootstrap方法是一类非参数Monte Carlo方法,其基本思想是根据样本的经验信息(分布),通过又放回的简单随机抽样获得B个bootstrap样本,进而利用这些Bootstrap样本信息进行统计推断。其中Bootstrap样本容量依然和原样本一致,且观测值被抽到的概率相等。当目标总体未指定的情况下,Bootstrap方法经常被使用,此时样本为唯一已有的信息。
Bootstrap方法的基本步骤为,假设x=(x1,x2,…,xn)为已知的一个样本,来自未知分布F。X*为从x中随机抽取的一个样本,通过有放回的抽样得到样本X*1,…,X*n,显然X*1,…,X*n服从{x1,…,xn}上的均匀分布,P(X*=xi)=1n,i=1,…,n。我们抽取简单子样本X*=(X*1,X*2,…,X*n),该样本为一个Bootstrap子样本。进行B次抽样,就可以得到B个Bootstrap样本。
另外,Bootstrap方法需借助计算机完成大量的模拟计算,通过足够多的重复抽样可以把样本均值的Bootstrap分布找出来,进而进行统计推断。
2.2 聚类分析
聚类分析思想是根据已知数据,观察各样品或变量之间亲疏关系的相似程度,依照某种准则,把一些相似程度较大的样品或变量聚合为一类,把另外一些相似程度较大的样品或变量聚合为另外一类,使同一类内差别较小,而类与类之间的差别较大,最终将观察样品或变量分为若干类。
聚类分析中需要进行相似性度量,通常用距离来衡量哪些样本应该聚为一类。我们假设有n个样本单位,每个样本测有p个指标(变量),每个样本都可以看成p维空间中的一点,n个样本就是p维空间中的n个点,第i个样本与第j个样本之间的距离记为dij,聚类过程中,相距较近的点归为一类,相距较远的点归为不同的类。其中dij满足条件:
dij≥0对一切的i和j成立,且仅当i=j时dij=0;
dij=dij对一切的i和j成立;
dij≤dik+dkj对于一切的i和j成立。
聚类中常用的距离有明氏(Minkowski)距离,马氏距离,具体的聚类的方法有系统聚类、模糊聚类、K均值聚类等等,其中系统聚类中常用的方法有最短距离法、最长距离法、中间距离法、重心法、离差平方和法等。综合考虑到数据是跨时间的面板数据,本文选用离差平方和法聚类。
3 实例分析
3.1 数据描述
商业银行的收益情况可以由其资产负债表反映出来,考虑到数据的可得性,本文选取了包括五大国有商业银行、中兴(CITIC)、光大(CEB)、兴业(IBC)、浦发(SHANG)、招商(CMB)、宁波商业银行(NCB)、深发展(SHENG)、华夏(HXB)、民生银行(CMBC)在内的14家银行作为研究对象,选取了2002年至2008年间银行的其他收入财产、总收入财产、固定资产、无收益资产、总资产、存款及短期资金、其他债券、其它免息财产、资产净值、总负责及股东权益、资产负债平衡、坏账准备金、流动性资产等13个指标考察各商业银行的收益水平情况。为消除部分数据缺失造成的影響,笔者在原有数据基础上采用Bootstrap方法,对原始数据进行重抽样计算得到各商业银行的13个指标的均值,简记指标名依次为COL1-COL13,具体数据见图1。
3.2 结果分析
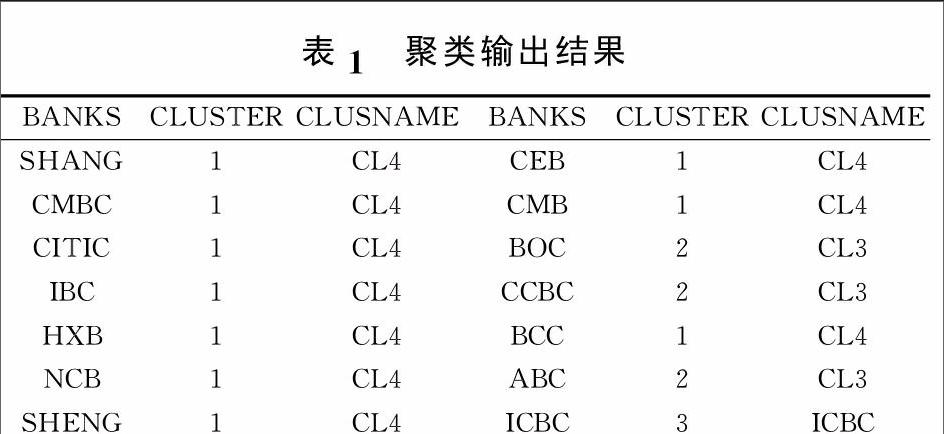
我们采用和离差平方和法利用SAS软件将14个商业银行的资产负债结构进行聚类分析,最终将其分为三个类别。运行以下SAS语句可以得到聚类的树状图以及分类结果。
proc cluster data=banks method=ward ccc pseudo;
var col1-col13;
id banks;
run;
proc tree horizontal ncl=3 out=out;/*out为分类结果输出数据*/
id banks;
run;
聚类树状图如图2所示:
对比聚类结果,可以发现部分的指标有减少的趋势。其中中国工商银行大部分指标都高于其他商业银行,一定程度说明了工行的优势地位。1类商业银行较工行存在不小差距,需要完善其資产负债的合理性。本文基于Bootstrap-聚类分析对商业银行的资产负债进行初步的分类,必须意识到各个商业银行都在发展中,该分类不是一劳永逸的。在此分类基础上,我们还可以进一步挖掘资产负债与银行盈利能力、金融稳定性等的关系。而且,随着时间的发展,我们还可以引入时间序列分析方法,进行多指标时间序列聚类。
参考文献
[1]Efron Bradley.Bootst rap methods : another look at the jackknife[J].The Annals of Statistics,1979,7(1):1-26.
[2]Efron Bradley,Tibshirani Robert.An introduction to the bootstrap[M].New York:Chapman & Hall Ltd,1993.
[3]Thomas J.DiCiccio and Bradley Efron.Bootstrap Confidence Intervals[J].Statistical Science,1996,(11).
[4]施锡铨.独立非同分布情况的光滑Bootstrap逼近[J].数学物理学报,1990,(10).
[5]赵亮,程锦秀.Bootstrap方法及其在生物学研究中的应用[J].四川动物,2010,(29).
[6]孙佳美,段白鸽.Bootstrap方法在死亡模型中的应用[J].统计研究,2010,(6).
[7]刘勤,金丕焕.Bootstrap方法及其在医学统计中的应用[J].中华预防医学杂志,1998,1(32):1.
[8]谢益辉,朱钰.Bootstrap方法的历史发展和前沿研究[J].统计与信息论坛,2008,(2):90-96.

