基于PSO优化BP神经网络的钻井动态风险评估方法*

管志川，胜亚楠，许玉强，王 庆，张 波

(中国石油大学(华东) 石油工程学院，山东 青岛 266580)

0 引言

钻井工程是石油天然气开发过程中十分重要的环节[1]。钻井作业也是高风险、高投入的工程作业，井下异常情况和风险随时都有可能发生，可能会影响到钻井速度、生产安全、工程质量和经济效益[2-5]。因此，应该做好钻井作业过程中动态风险的预警工作，在风险发生的早期给出一定意义上的风险提示，采取有效措施规避可能发生的钻井工程风险，从而科学有效地保证钻井作业顺利进行。传统的钻井动态风险评估方法有：层次分析法、事故树法、模糊判别法、压力不确定性分析法以及案例分析法等[6-12]，这些方法依赖于专家经验，得到的结果多是定性或半定量的，已经无法满足当前深井复杂地层或深水环境钻井的安全需求。因此，如何建立1套不严重依赖于专家主观判断的钻井作业动态风险评估方法是值得研究的问题。BP神经网络具有高度自学习、自修正能力，其优点可以满足钻井工程动态风险评估的要求，因此利用BP神经网络实现钻井作业动态过程中的风险评估，并利用PSO算法弥补BP神经网络的缺陷，建立了基于PSO粒子群算法优化BP神经网络的钻井动态风险评估模型。该模型通过对录井资料的监测分析，实时判断井下风险类型，并计算风险发生概率，可以在风险发生的早期给出预警信息，及时指导风险调控措施的开展。

1 钻井作业过程动态风险评估理论基础

1.1 BP神经网络

BP神经网络是1种典型的人工神经网络系统[13-14]，最主要的优点是最有较强的非线性映射能力，这使得其适合于求解内部机制复杂的问题；同时，BP神经网络具有高度自学习、自修正能力，可以满足钻井工程动态风险评估的要求，因此，利用BP神经网络来实现钻井作业动态过程中的风险评估。

1.1.1 BP神经网络拓扑结构

BP神经网络是由输入层、隐含层和输出层构成的三层前向人工神经网络，如图1所示，其中，输入层有n个神经元，隐含层有l个神经元，输出层有m个神经元。

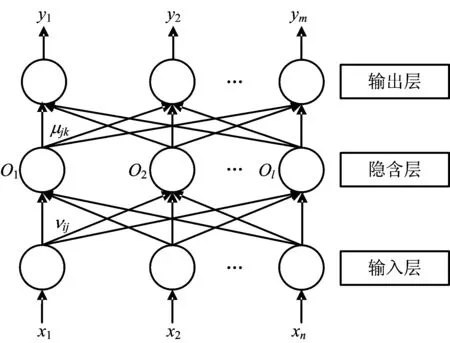
图1 BP神经网络示意Fig.1 Schematic diagram of BP neural network

根据神经元输出信号的计算公式可以得到隐含层各个神经元的输出为：

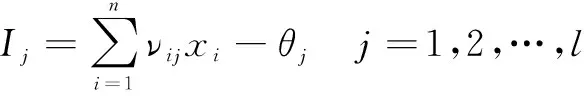
(1)

式中：νij是输入层神经元i和隐含层神经元j的连接权重；θj是隐含层神经元j的阈值；f()是神经元的激活函数。

同理，得到BP神经网络的输出层的输出信号为：

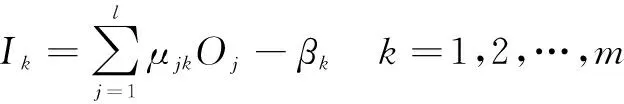
(2)

式中：μjk是隐含层神经元j和输出层神经元k的连接权重；βk是输出层神经元k的阈值；f()是神经元的激活函数。

1.1.2 BP神经网络学习算法

标准的BP网络采用的是最速下降法算法，是1种非线性回归模型参数最小二乘估计的1种迭代算法。BP神经网络的学习过程是通过学习动态地调整输入层、隐含层和输出层神经元之间的连接权重νij，μjk，以及隐含层和输出层神经元的阈值θj，βk，从而得到与实际期望相符合的输出值。

1.2 基于粒子群算法(PSO)改进BP神经网络

BP神经网络在过程控制、故障诊断、预测预报和非线性仿真问题中得到了很好的应用；同时，BP神经网络也有缺陷，比如BP神经网络采用梯度下降法，误差训练函数不是严格的凸函数，导致BP算法在寻找最优连接权值和阈值时，容易陷入到局部最小点，无法得到全局最优解，这就影响了BP算法预测结果的准确性；因此，应当寻找1种优化算法来弥补BP神经网络的缺陷。通过调研文献发现，粒子群优化算法适合于解决寻找全局最优解的问题，因此利用粒子群算法(PSO)的全局搜索最优解的能力来弥补BP神经网络局部寻优的缺陷，利用粒子群优化算法对神经网络的各层神经元之间的连接权值和阈值进行优化。粒子群优化算法是模拟鸟群寻找栖息地的行为，通过搜索各个粒子的优解和利用这些优解使整个粒子群达到最优的过程[15-16]。

1.2.1 粒子群算法(PSO)原理及数学模型

PSO是基于群体智能理论的优化算法。每个粒子代表解空间的1个候选解，解的优劣程度由适应函数决定。在粒子群算法的寻找最优解的过程中，需要首先根据实际问题确定维度，假设在1个D维空间内进行最优解的寻找与搜索，设定初始化有M个粒子，这些粒子组成1个待研究的“鸟群”T={Z1,Z2,…,ZM),i=1,2,…,M，其中，zi=(zi1,zi2,…,ziD),i=1,2,…,M，表示第i个粒子在D维空间内的位置向量，si=(si1,si2,…,siD),i=1,2,…,M表示第i个粒子在D维空间内的速度向量；粒子自身的飞行运动经验，也就是截止到目前为止搜索到的个体粒子的最优位置表示为Pbesti=(Pbesti1,Pbesti2,…,PbestiD)，全局最优位置为Gbest=(Gbest1,Gbest2,…,GbestD)。粒子位置的更新由4部分组成：粒子当前位置和速度、粒子当前位置与Pbesti，Gbest的距离。因此，粒子算法的递推公式为：

(3)

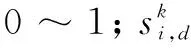
1.2.2 基于粒子群算法改进BP神经网络

用粒子群算法优化BP神经网络，主要是通过粒子群的迭代取代BP神经网络的梯度下降法。基于PSO优化BP神经网络的主要步骤如下：

1) 初始化参数。确定BP神经网络拓扑结构，初始其连接权值和阈值，根据其权值和阈值的个数确定粒子群维数D；设置种群规模M；设置迭代次数N；对神经网络权值和阈值进行实数编码，得到初始种群；并且在允许范围内[smin,smax]，[zmin,zmax]内设定粒子速度si,d和位置zi,d；然后，设置学习因子c1，c2。

2) 将神经网络中每次迭代得到的均方误差作为粒子的适应度函数。

3) 根据粒子群算法的步骤2)～4)，求解粒子全局最优位置。

4) 检查是否满足迭代终止条件，若满足，则停止，输出最优粒子，反解码得到最优权值和阈值。

5)按照BP神经网络进行训练和预测。

2 基于PSO优化BP神经网络的钻井动态风险评估模型

2.1 钻井动态风险评估模型的设计

2.1.1 BP神经网络结构的设计

选用BP神经网络法，结合综合录井参数建立钻井作业过程中动态风险评估模型。首先应明确BP神经网络的结构，即从解决钻井动态风险评估的实际问题出发，分别对输入层、输出层和隐含层进行科学合理的设计。

1)输入层设计

任何一种钻井工程风险的发生均需要一定的时间，在该风险发生的初始阶段，会出现不同的录井参数特征发生变化，这些风险均对应有不同的特征参数(见表1)。对于钻井事故及风险与录井参数之间的关系国内外技术人员开展了大量的研究工作。

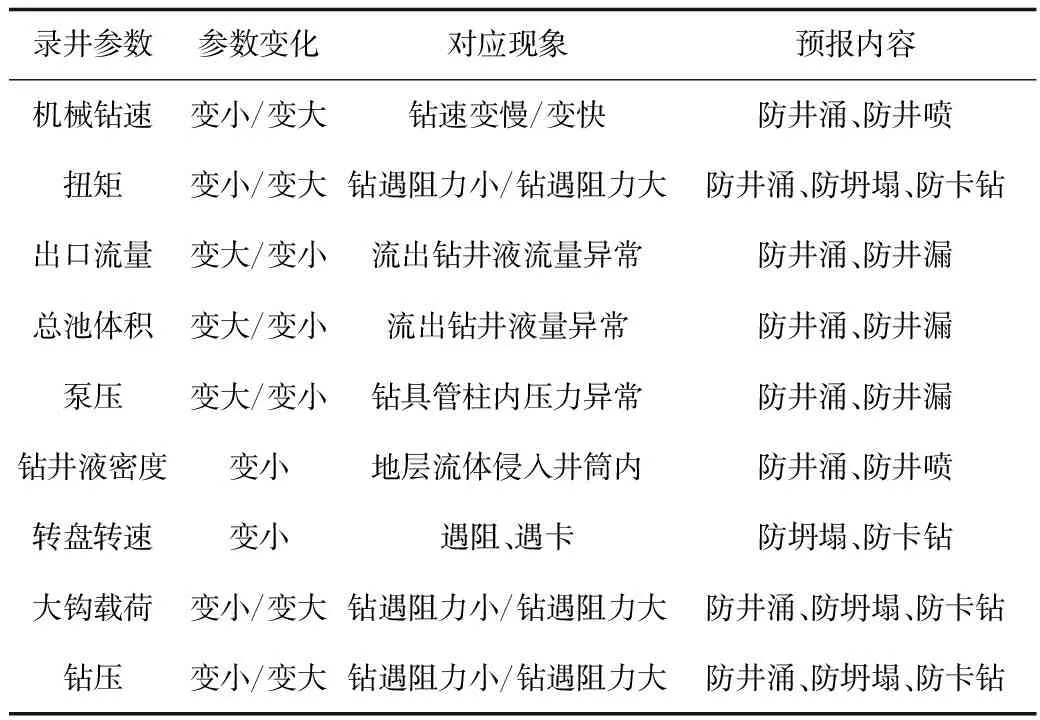
表1 井下风险与录井参数变化的对应关系

在前人研究的基础上，根据井下异常及工程风险专家知识，去掉与钻井工程风险相关性较小的录井特征参数，同时综合兼顾4种风险的表征录井参数，最终设定9个录井特征参数作为BP神经网络的输入神经元，即：钻井液出口流量、钻井液出口密度、钻井液池总体积、泵压、大钩载荷、机械钻速、转盘转速、扭矩、钻压。

2)输出层设计

重点以井涌、井塌、井漏和卡钻风险为主进行钻井作业动态风险评估。因此有5个输出神经元：井涌、井塌、井漏、卡钻和正常。5种井下状态所对应的期望向量为：q1=(1,0,0,0,0)，q2=(0,1,0,0,0)，q3=(0,0,1,0,0)，q4=(0,0,0,1,0)，q5=(0,0,0,0,1)。

3) 隐含层设计

在BP神经网络中，一般都是设计1个隐含层，增加隐含层的目的是为了进一步降低输出结果的误差、提高精度；但是，增加隐含层层数会导致BP神经网络结构更加复杂，致使网络训练时间增加。研究证明：增加隐含层神经元的个数，同样可以降低误差、提高精度。结合钻井动态风险评估问题的实际，只考虑1个隐含层，采用经典的3层BP神经网络结构解决问题。隐含层的个数初步由经典公式(4)计算得到，然后再结合钻井动态风险评估实际问题的网络训练情况进行优选。

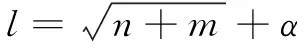
(4)

式中：n为输入层节点数；l为隐含层节点数；m为输出层节点数；α取值为1～10。

建立的BP网络输入层节点数n=9，输出层节点数m=5，根据经验公式计算得到隐含层神经元节点个数l∈[3,17]。为了确定最佳隐含层节点数，将隐含层节点数分别设置为3～17的BP网络分别进行训练，最终确定使得网络误差最小的节点数为10。

最终建立了BP神经网络结构，如图2所示。

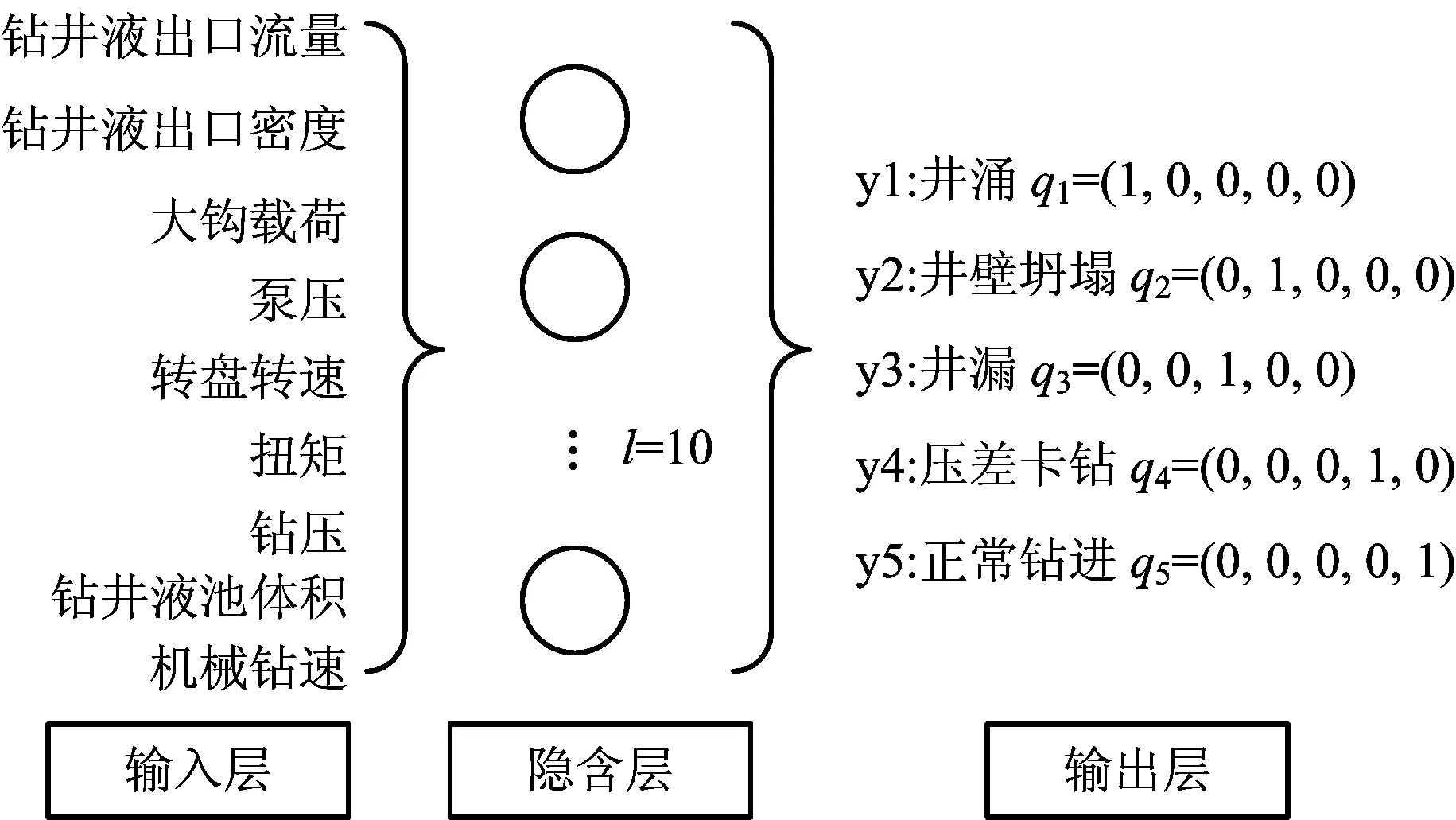
图2 钻井动态风险评估BP神经网络结构Fig.2 BP neural network structure for dynamic drilling risk assessment

2.1.2 粒子群算法设计

BP神经网络动态风险预测模型确定后，下面进行粒子群算法的设计，主要包括粒子编码、适应度函数以及算法关键参数的确定。

1) 粒子编码

在粒子群算法优化BP神经网络时，神经网络中的连接权值和阈值对应粒子种群中的粒子。在上一节中，已经确定神经网络结构中各层神经元的节点数分别为，输入层节点数n=9，输出层节点数m=5，隐含层节点数l=10。神经网络结构为9-10-5，所以，共有9×10+10×5=140个权值，10+5=15个阈值。则粒子群优化参数的个数为155个，粒子的长度为155，网络结构如图3所示。

采用向量编码，粒子i被编码为：

particle(i)=

(5)

则BP神经网络初始权值和阈值的寻优过程就转化成粒子的进化过程。

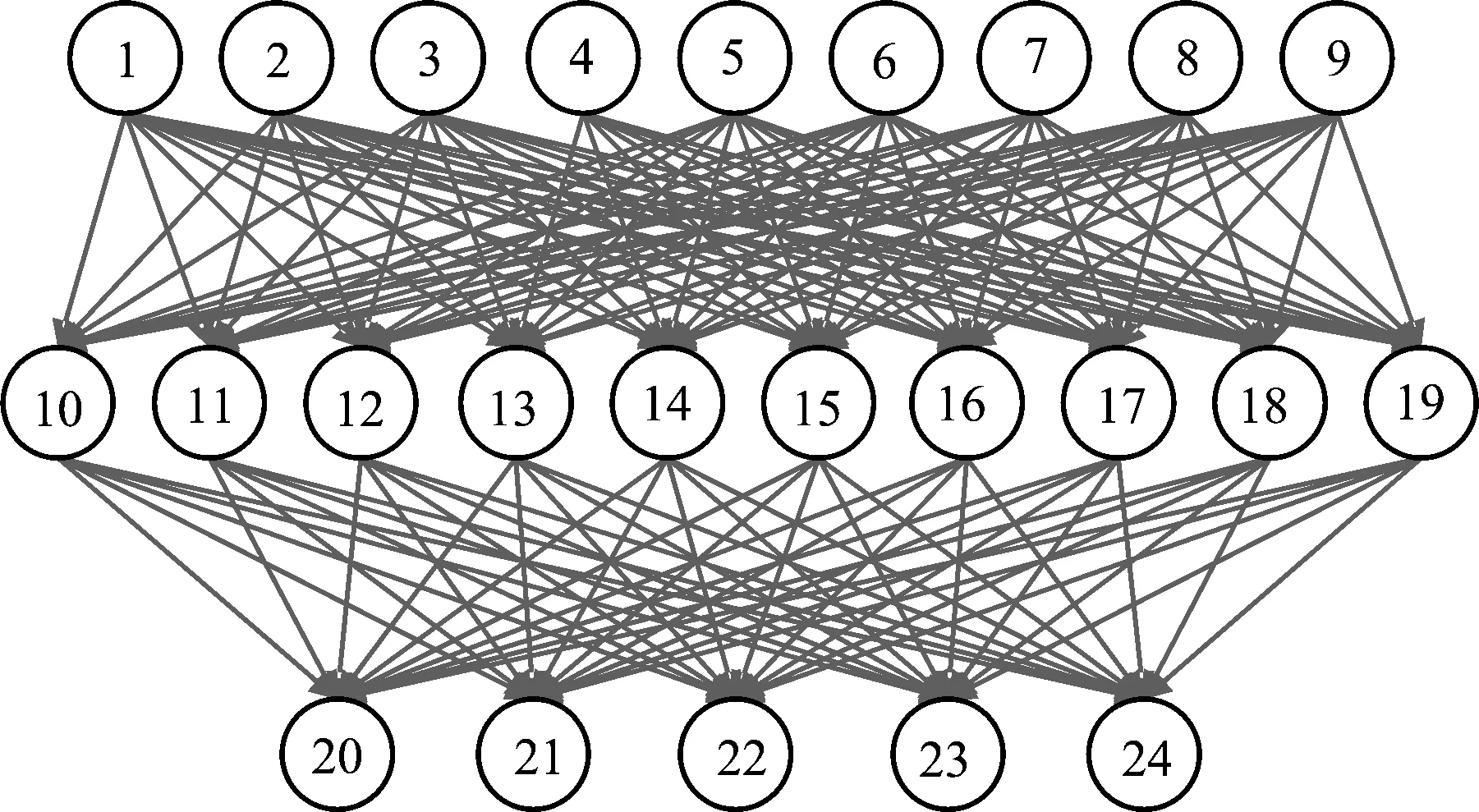
图3 基于粒子群算法优化钻井动态风险评估BP神经网络Fig.3 Optimized BP neural network based on Particle Swarm Optimization for dynamic drilling risk assessment

2)适应度函数

权值和阈值的优化就是为了减少网络训练误差，因此将BP网络训练的均方根误差作为适应度函数。

(6)

式中：M为训练样本个数；l为输出层神经元个数；yj,i为第i个训练样本第j个输出节点的实际输出值；qj,i为第i个训练样本第j个输出节点的理想期望输出值。

3) 粒子算法关键参数

需要初始化的关键参数：种群规模M=30；迭代次数N=100；在速度和位置允许范围内[smin,smax]，[zmin,zmax]内进行粒子速度si,d和位置zi,d的随机初始化；学习因子c1=2.0，c2=2.0。

2.2 录井数据处理

不同录井参数数据之间的量级差别较大，因此需要对录井资料进行数据归一化处理，消除神经网络输入层各个数据的量级差别，避免因为输入输出数据数量级差别较大而造成网络预测误差较大，基于最大最小法对录井参数进行归一化处理。结合海上BD气田已钻井典型风险对应的录井资料，选取风险发生前后一段时间内录井参数进行归一化处理，如表2所示。

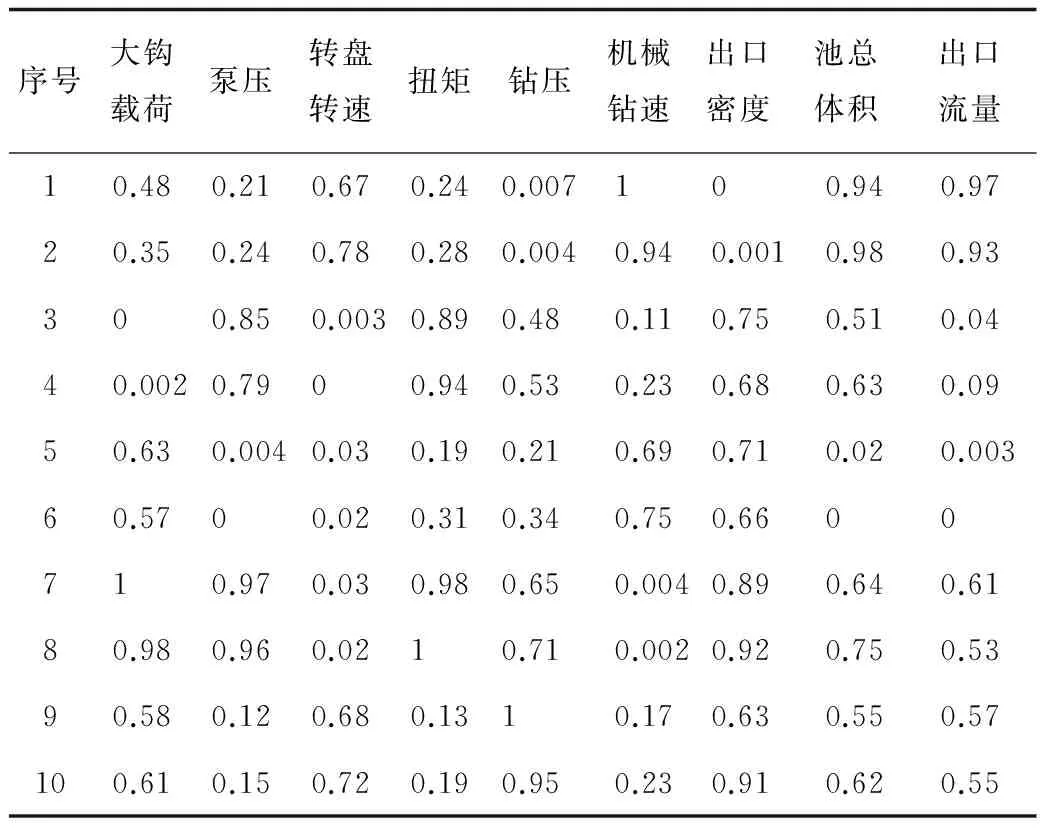
表2 录井参数归一化处理结果

2.3 风险模型学习训练与结果分析

2.3.1 算法基本控制要素

采用PSO优化BP神经网络算法的基本控制要素如表3所示。

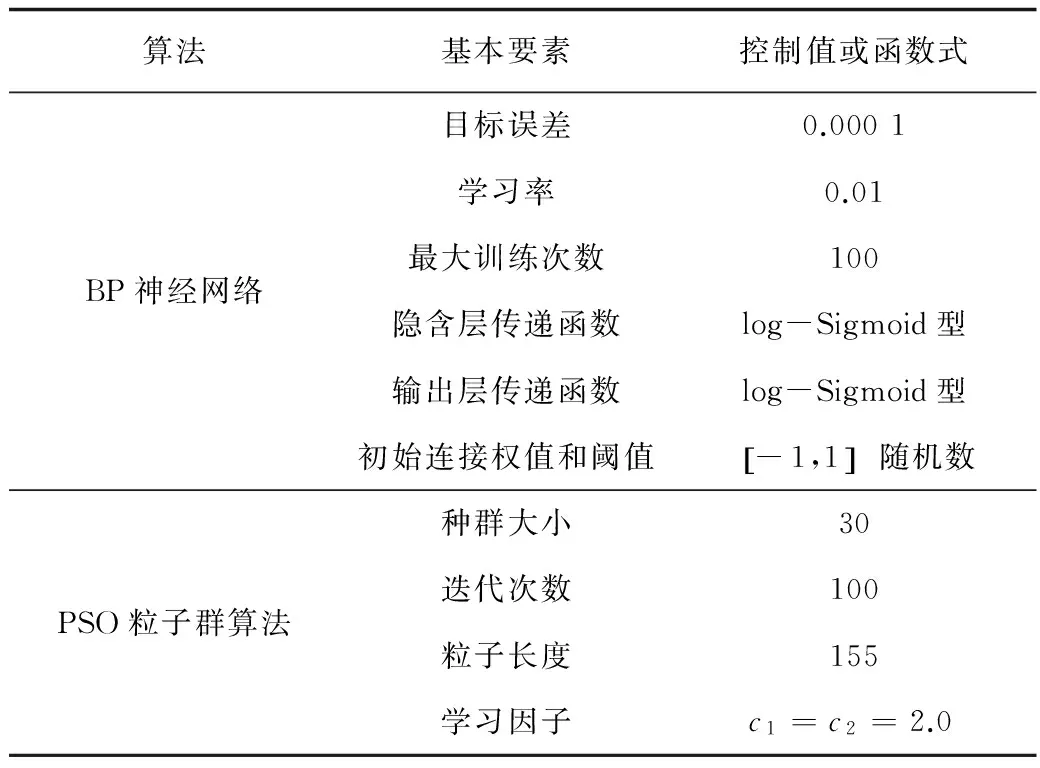
表3 PSO优化BP神经网络算法的基本控制要素

2.3.2 网络训练仿真与结果分析

选取BD区块10组录井归一化数据以及相对应的井下钻井状态作为训练样本，对动态风险评估神经网络进行训练，网络训练样本如表4所示。

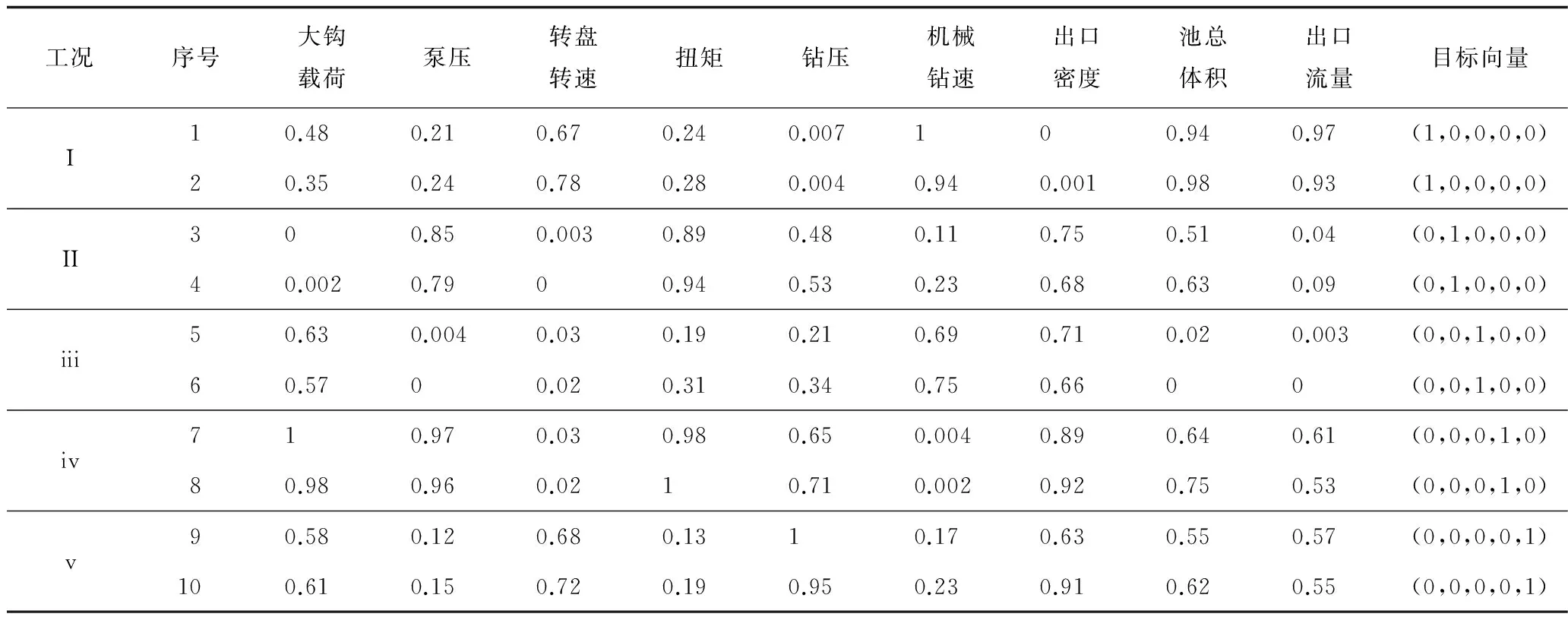
表4 网络训练仿真样本

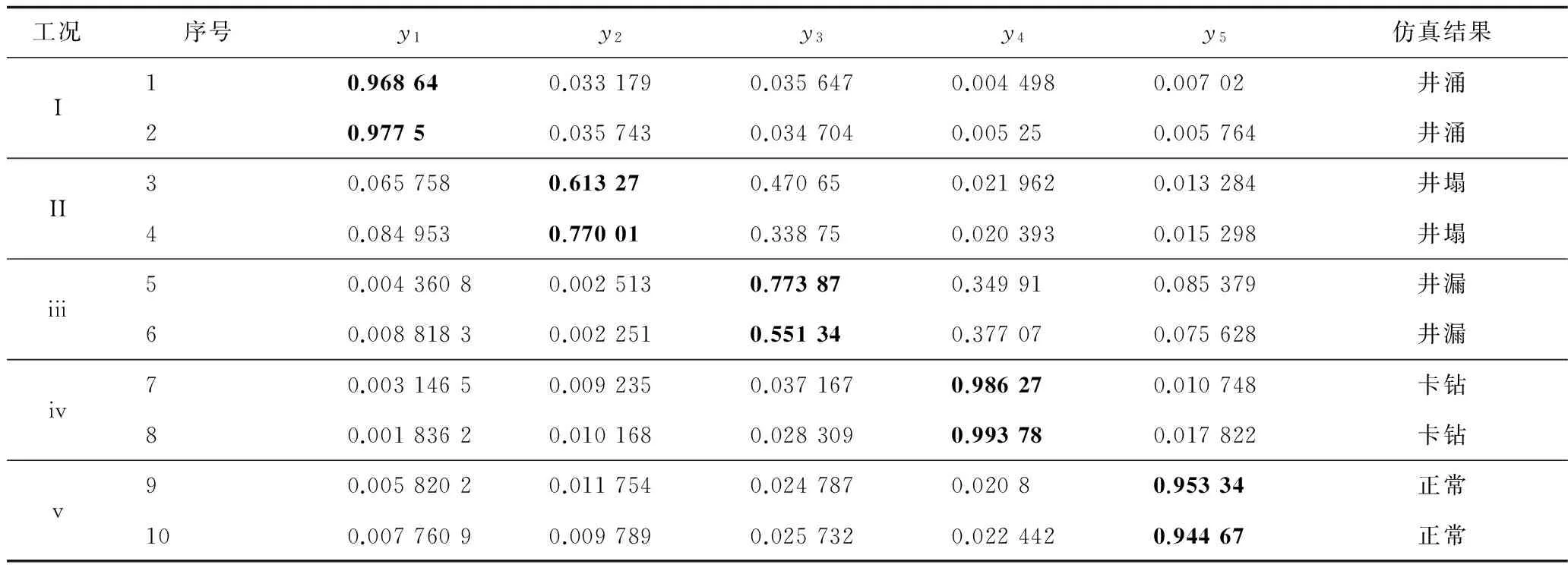
表5 动态风险评估神经网络训练仿真结果

表5中，y1，y2，y3，y4，y5分别对应井涌、井塌、井漏、卡钻和正常状态；并且每一行最接近1的数值(表5中加粗)所对应的结果即是仿真预测的井下风险类型。根据表5的网络仿真结果可以得到如下结论：10组仿真结果全部与实际井下实际状态相吻合，表明训练得到的神经网络具有很高的可信度，能够很好地满足该区块该层段钻井风险动态评估的要求。

值得注意的是，建立的风险动态评估模型具有一定的适用性：在不同的地质环境以及不同的钻进条件下，井下异常状态或风险对应的录井参数的变化会有所区别，所以在选取训练样本时，应该根据不同钻井环境和钻遇的地层条件进行选择，并且训练得到的神经网络只运用于相似钻井条件下的异常工况及风险诊断。

3 动态风险评估实例分析

BD气田是中海油海外重要的高温高压气田之一，其储层为礁灰岩，储层以上为大段泥岩、页岩、泥灰岩、薄层砂岩，地质环境复杂；BD气田前期2口探井在钻井施工过程中频繁出现井下复杂情况和事故，严重影响了钻井安全高效的进行。因此，有必要针对BD气田开展钻井动态风险评估。

选取BD气田BD A井待分析评估的风险井段对应的录井参数，首先进行归一化处理，构建分析样本，如表6所示；然后代入训练好的适用于BD区块的动态风险评估模型中进行风险评估实例分析，结果如表7所示。实例分析结果表明，动态风险评估结果与实际风险相互吻合。说明本文建立的方法可以很好地对钻井作业过程中动态风险进行评估，可以及时对可能发生的风险进行预警，并采取控制措施，能够有效地降低钻井过程中风险发生的概率及抑制钻井风险程度的恶化，对于安全高效钻井具有重要意义。

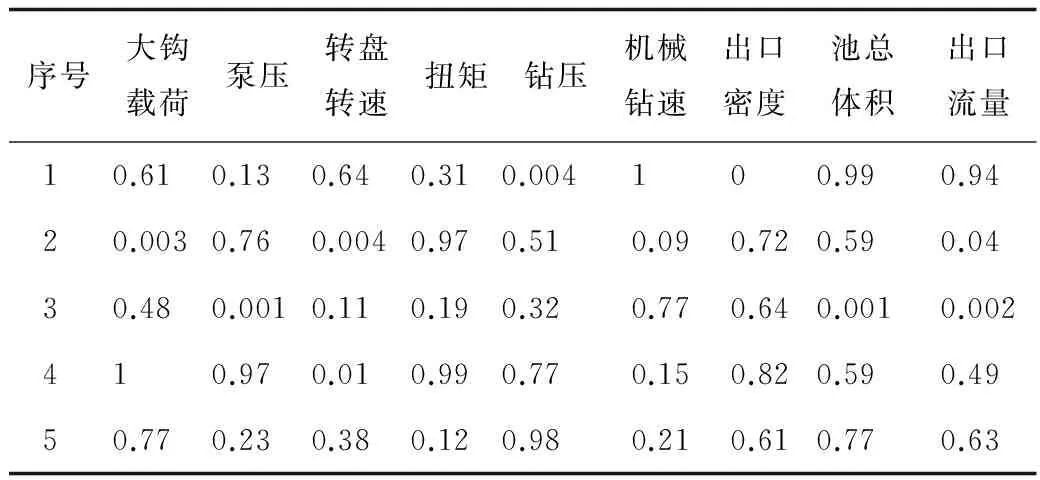
表6 待评估井段录井参数归一化结果

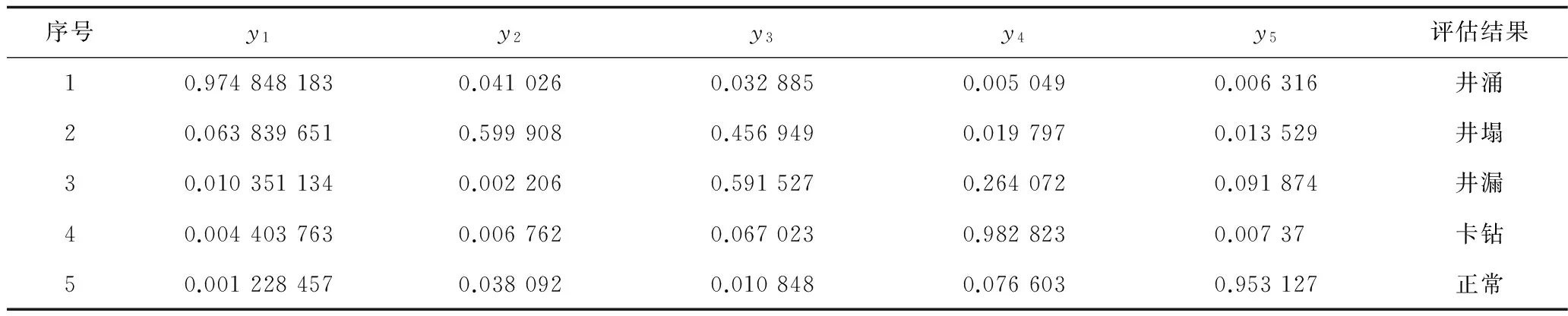
表7 神经网络钻井动态风险评估结果

4 结论

1)BP神经网络的误差训练函数不是严格的凸函数，导致在寻找最优连接权值和阈值时，容易陷入局部最小，无法得到全局最优解；BP网络的缺陷影响了动态风险评估结果的准确性；基于PSO粒子群算法的全局搜索最优解的能力可以弥补BP神经网络局部寻优的缺陷。

2)通过对录井资料的监测分析，基于人工智能的理论及方法，实时判断井下风险发生的类型，并定量计算风险概率，建立了基于PSO优化BP神经网络的钻井动态风险评估模型。相比较传统风险评估的定性、半定量结果而言，构建的定量评估模型在解决深井复杂地层或深水环境钻井过程中的风险预测问题方面更具有优势。

3)采用所建立的模型对BD气田进行实例分析，10组仿真结果全部与实际井下实际状态相吻合；同时，5组预测结果也全部与实际风险相互吻合，结果表明动态风险评估结果与实际风险相互吻合，说明采用建立的方法得到的风险预测结果具有较高的可信度，对于安全高效钻井具有参考意义。

[1] 陈庭根,管志川.钻井工程理论与技术[M]. 东营：石油大学出版社,2000: 251-254

[2] Bratton T, Edwards S, Fuller J, et al. Avoiding drilling problems [J]. Oilfield Review, 2001, 13(2):75-77.

[3] Ismail Z, Kong K K, Othman S Z, et al. Evaluating accidents in the offshore drilling of petroleum: regional picture and reducing impact[J]. Measurement, 2014, 51(1):18-33.

[4] Moos D, Peska P, Finkbeiner T, et al. Comprehensive wellbore stability analysis utilizing quantitative risk assessment [J]. Journal of Petroleum Science & Engineering, 2003, 38(4):97-109.

[5] 增义金,刘建立.深井超深井钻井技术现状和发展趋势[J].石油钻探技术,2005,33(5):1-5.

ZENG Yijin, LIU Jianli. Present situation and development trend of deep and ultra-deep well drilling technology [J]. Petroleum Drilling Technology, 2005, 33(5):1-5.

[6] 蒋希文.钻井事故与复杂问题[M].2版. 北京：石油工业出版社，2006.

[7] 高德利.复杂地质条件下深井超深井钻井技术[M].北京：石油工业出版社，2004.

[8] Khakzad N, Khan F, Amyotte P. Quantitative risk analysis of offshore drilling operations: A Bayesian approach [J]. Safety Science, 2013, 57(57):108-117.

[9] 管志川,柯珂,路保平.压力不确定条件下套管层次及下深确定方法[J].中国石油大学学报(自然科学版),2009,33(4):71-75.

GUAN Zhichuan, KE Ke, LU Baoping. An approach to casing program design with formation pressure uncertainties [J]. Journal of China University of Petroleum (Natural Science Edition), 2009, 33(4):71-75.

[10] Qiang L I, Zhang J, Xiao R J, et al. Tracing analysis on long distance transmission pipeline girth weld quality causes-based on analytical hierarchy process(AHP)[J]. Welded Pipe & Tube, 2007(1)：67-71，86.

[11] Guan Zhich uan , Ke Ke , Lu Baoping .A new approach for casing program design with pressure uncertainties of deepwater exploration wells[R] .SPE 130822, 2010 .

[12] 袁智, 汪海阁, 王海强,等. 基于事故树分析的钻井井漏事故危险评价研究[J]. 中国安全科学学报, 2010, 20(3):107-112.

YUAN Zhi, WANG Haige, WANG Haiqiang，et al. Application of fault tree analysis to risk assessment of lost circulation hazards in drilling[J]. China Safety Science Journal, 2010, 20(3):107-112.

[13] 高隽. 人工神经网络原理及仿真实例[M]. 北京：机械工业出版社, 2007.

[14] 苏高利, 邓芳萍. 论基于MATLAB语言的BP神经网络的改进算法[J]. 科技通报, 2003, 19(2):130-135.

SU Gaoli, DENG Fangping. On the improving backpropagation algorithms of the neural networks based on MATLAB language: a review [J]. Bulletin of Science and Technology, 2003, 19(2):130-135.

[15] 杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5):87-94.

YANG Wei, LI Qiqiang. Overview of particle swarm optimization algorithm [J]. China Engineering Science, 2004, 6(5):87-94.

[16] 纪震, 廖惠连, 吴青华. 粒子群算法及应用[M].北京：科学出版社, 2009.