挖掘数学教材,培养探究能力
福建省上杭县第三中学 陈尚宽
挖掘数学教材,培养探究能力
福建省上杭县第三中学 陈尚宽
教材既是教育之“材”,又为课时之“本”。挖掘教材,是优化教学设计、高效课堂教学的基石,是教师专业成长的“快车道”。教师只有以生为本,与时俱进,钻研教材、感悟教材、领会教材,即真正“品其味,悟其神”,才能挖掘教材资源的深层价值,进而创造性地开发和使用教材,引领学生探究创新,提升学生数学素养。
怎样才能充分挖掘初中数学教材,提升课堂教学魅力,创建自主探究平台,培养学生探究能力?下文是笔者在初中数学教学实践中的一些体会。
一、引申【探究】,激趣质疑
人教版数学教材中的【探究】栏目给学生提供了思维发展、合作交流的空间,搭建了一个探究、创新的舞台。但学生探究要有欲望来支撑,而欲望要用“情境”来“激活”,所以在课堂教学中,教师应根据【探究】栏目的内容加以引申,以现实逼真的情景引入课堂,使数学真正融入情境,让课堂充满情趣,进而激发学生的探究质疑。
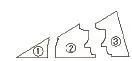
如人教版八年级数学上册“三角形全等的判定”中的【探究4】,在课堂教学时,我首先创设这样的情景:“老师刚刚不小心打碎了一块三角形玻璃,它碎裂成如下的三块。现要重新配置,请同学们帮老师出主意,要带哪块去,才能配置出一模一样的玻璃出来?”学生一听到这个关于现实生活的问题,立即有了兴趣,主动参与,纷纷动手画起来,从而进入最佳的学习状态,为主动探究新知和合作交流聚集动力。
教师为教材中的【探究】栏目创设情景,激趣质疑,把探究的第一棒交给学生,并珍视学生独特的感受、体验和理解以及由此而萌生的与人交流的冲动。这种探究不是老师强加的“为赋新诗强说愁”,而是学生逼真情境中的自然需求,这时课堂才是美丽的,探究才是有效的。
二、拓展【例题】,活化思维
教材中的【例题】具有典范作用,极具探究价值,但探究要找准“接受”经典过程的“距离”,用“问题”来“架桥”。教师应充分挖掘【例题】内蕴,巧妙拓展延伸,通过对例题的条件发散或结论发散或相似问题的递进研究,精心设计问题,启发引导学生发散探索,从而活化思维。
如九年级数学上册“直线和圆的位置关系”中的【例2】:如图(1)所示,△ABC的内切圆⊙O与BC、CA、AB分别相切于D、E、F,且AB=9,BC=14,CA=13,求AF,BD,CE的长。

教学中,我将原例题拓展加工,设计如下几个问题:
问题1 如果已知条件改为BC=a,AC=b,AB=c,那么AF,BD,CE的长应该分别怎样表示?
问题2 如图(2)所示,若∠A=60°,则∠FOE为多少度?∠FDE为多少度?若∠A=α呢?
问题3 △ABC可以是锐角三角形、直角三角形、钝角三角形,而△DEF是否也是这样?
问题4 如果已知条件改为BC=a,AC=b,AB=c,⊙O的半径为r,那么△ABC的面积与△ABC的周长、内切圆的半径之间有什么关系?
问题5 边长3,4,5的三角形能覆盖多大的圆?
问题6 如果已知条件改为∠C=90°,BC=a,AC=b,AB=c,那么△ABC的内切圆的半径r是多少?
问题7 如果过△ABC的内心的直线l把△ABC周长两等分,那么l能否把△ABC面积两等分?
问题8 如果直线l将△ABC的周长和面积都平分,那么l是否过△ABC的内心?
在教学中,教师根据教材中的【例题】精心设疑,通过提问,由浅入深、环环紧扣地引导学生释疑,使学生体验数学过程,培养探索意识,激发积极思维,让学生感到自己是一个发现者、研究者、探索者。
三、类比【归纳】,迁移变换
教材中的【归纳】栏目主要是对数学内容的重点进行总结,有一个一般性的结论,对整节课或整章节的学习有指导性作用。而类比是一项探索性或发现性活动,它是提出问题、发现新知的主要源泉,是科学研究最普遍的方法。在教学中,教师可根据【归纳】栏目的结论,细致琢磨,深入推敲,紧扣结论,类比变换,精心设计问题,引导学生探索,实现知识的迁移,达到举一反三,触类旁通的目的。
如九年级数学上册“关于原点对称的点的坐标”中的【归纳】:两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P'(-x,-y),亦即点P(x,y)绕原点旋转180°后对应点的坐标为(-x,-y)。
教学时,我在此结论的基础上类比设计以下问题,引领同学们进行探究:
问题1 你能否利用所学的知识来证明此结论?
问题2 如果点P(x,y)绕原点顺时针旋转90°,那么点P的对应点的坐标是怎样?你能否直观形象地描述出来?
问题3 如果点P(x,y)绕原点逆时针旋转90°,那么点P的对应点的坐标是怎样的?你能否直观形象地描述出来?
在教学中,教师要启发学生充分利用教材中的【归纳】栏目的结论,从知识的顺延、从属、引申、互逆、相似等方面考虑和发掘类比因素,抓住新旧知识的共同性质加以分析、比较,同时逐步引导学生由“已知”发现“未知”,从而使学生在类比推理、迁移变换的探究活动中,体会到这是对教材感悟体验的释放,这也是类比中情感智慧的升华!
四、【阅读思考】,勇于探究
教材中的【阅读与思考】等选学栏目,为学生提供了通今达古、博大精深的数学天地,具有丰富的教育教学功能。在教学中,教师应充分挖掘【阅读与思考】等栏目奥妙无穷的素材,拓宽学生知识视野,提炼数学思想方法,引导学生通过数学实践、主动阅读、独立思考,大胆猜想,勇于探究,掌握科学的思维方法,提高数学思维能力。
如八年级数学上册“完全平方公式”中的【阅读与思考】“杨辉三角”,我利用其中的公式设计了如下问题:
解:由a3+b3+c3=0 可得:(a+b)3-3ab(a+b)+c3=0,
∴(-c)3+3abc+c3=0,
∴3abc=0,∴a=0或b=0或c=0,
不妨设a=0,则b=-c,
∴a5+b5+c5=0+(-c)5+c5=0。
问题解决后,教师又提问:问题2 已知不变,你能否求出a7+b7+c7的值呢?
问题3 比较上述结论,结合已知条件,请你大胆猜想一下a2015+b2015+c2015的值是多少。
问题4 你能不能用一般式来表示你的猜想,并证明你的结论?
像本例就涉及观察—分析—综合,联想—猜想,特殊—一般等思维方法。教师利用教材中的【阅读与思考】栏目内容精心编制问题,通过设问引导学生进行探索,获取解决问题的思维方法,达到发挥教材【阅读与思考】等栏目培养学生思维方法,增强学生探究能力等的教育教学功能。
因此,在新课程理念下,挖掘数学教材,培养探究能力,正是我们教师应深思和值得研究的一个重要课题。在初中数学教学中,教师应高度重视把教材作为载体和资源,源于教材,活于教材,高于教材,进而引领学生像“小科学家”一样,以主人的身份去发现问题、解决问题,并在探究的过程中获取知识、发展技能、培养能力。

