追问：将数学思维引向纵深处

江苏省淮阴师范学院第一附属小学 陈志凤

追问：将数学思维引向纵深处

江苏省淮阴师范学院第一附属小学 陈志凤

“问题”是数学的心脏，是学生思维的动力源泉，没有问题就没有思维，所以，课堂教学就是围绕解决问题来展开的，而解决问题，就少不了学生思维的参与，少不了师生之间的互动。提问是教学过程中师生之间经常发生的—种对话，“追问”是其中很重要的一种，是在提问的基础上进行的。“追问”作为前一问题的延伸，被更广泛地运用于各个教学环节。数学课堂中善于追问的老师，一定是有学生立场的教师，在尊重学生已有思考的基础上，通过追问，将学生思维引向纵深处。

一、在关键处追问，用“追问”来启发学生的思维

“追问”的价值在于探明学生的思维状态，促进思维能力的提升。思维的参与是学生参与数学课堂的最高境界，平时应该提供给学生充分思考和表达的空间，对学生正确的答案及时进行追问，从而引导学生及时还原思考过程，提升思维能力。我们平时的课堂中，经常在学生回答了问题之后追问“你是怎么想的？说说你的理由？为什么？”等等这些看似简单的问题，却能触发学生思考的本原，让学生在老师有意识地引领下积极思维。

下面是三年级《认识长方形和正方形》的教学片段：

师：（出示教室情境）找一找教室里的长方形，正方形。

生：教室黑板的面是长方形，课桌的面是长方形，窗户的面是正方形……

师：生活中，你在哪里见过长方形和正方形？

生：家中电视机的面是长方形，魔方的一个面是正方形……

揭题：生活中有那么多的长方形和正方形，它们有什么特征呢？今天这节课就来研究长方形和正方形的特征。

师启发：可以从哪些方面去研究长方形和正方形呢？

生：边和角。

追问：你打算怎样研究边？怎样研究角？

生讨论，交流。

师生小结方法：量一量，折一折，比一比……

学生操作活动：研究长方形边和角的特点。

……

我们知道，长方形和正方形的特征不是由老师直接给学生的，而是学生在丰富的操作活动中探究发现的，所以课中安排了大量的时间让学生充分操作，但如果没有明确的操作方向和要求，学生的操作可能是无效的活动，所以在学生已经知道要从“边和角”两个方面去研究长方形和正方形时，我没有满足，而是继续对学生操作的方法进行追问：你打算怎样研究边？怎样研究角？学生在讨论、交流中明确方法，也许学生会一时语塞，但却活跃了学生的思维，使学生的思维没有仅仅停留在表面，而是变得更深刻，更为后续学生操作活动的高效提供了保证。

在平时的课堂中，不能因为学生的回答是正确的就止步，应该多去听一听他们是怎么想的，这样才能还原他们的思考过程，从而更好地为老师提供更多的教学资源。如果我们在课堂中缺少追问，那么就可能无法知道学生的真实想法，也就不能及时调整我们的课堂教学。

二、在易错处追问，用“追问”让学生思维更缜密

学习的过程往往是一个“试误”的过程，“试误”的目的旨在暴露学生的思维过程。“错误”中往往孕育着比正确更丰富的教学资源，它是学生最朴实的思想、最真实的经验，往往是一种鲜活的教学资源，我们要善于挖掘和发现错误背后隐藏的教学价值，引导学生从错中求知，从错中探究，从而引导学生全方位、多角度地思维，使思考方法不断优化，让学生学会合理地调整思维方向。

如：在教学二年级上册《表内除法》时，教材中安排了这样两道题：

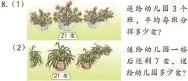
因为这段学习内容是表内除法，学生在做这两道题时总是习惯性思维，所以列算式：（1）21÷3=7（盆）；（2）21÷7=3（盆）。

针对学生的思维错误，课堂上我这样讲解：

提问：这两个问题一样吗？每个问题应该怎样想？

生无语，发愣。（生没有发现两个问题的不同）

追问：仔细读一读每道题，每道题中的数量关系是怎样的呢？

生读题，思考。

引导发现：问题（1）“把21盆花平均分给幼儿园的3个班”，这是“平均分”的问题，用除法计算；问题（2）“把21盆花送给幼儿园一些后还剩7盆”，这是已知总量和部分量，求部分量的问题，应该用减法计算，列式为：21-7=14（盆）。

这儿的追问看似平淡，但这绝不是一般的对话，对话是平铺直叙地交流，而“追问”是对事物的深刻挖掘，是逼近事物本质的探究，是促进学生思考的催化剂。通过对两道题中数量关系的分析，让学生明白了错误的原因，理解了每道题的计算方法。在教学中，只是让学生判断对或错是远远不够的，要通过教师的有效追问让学生明白对或错的成因，找出问题的症结，从而有利于从本质上去理解数学知识，解决数学问题。

三、在对比中思考，用“追问”探寻数学知识的本质

课堂上学生对知识的理解可能表面化、浅层化，不能深入思考，这时候,我们就可以用追问的方式来推进学生的思维不断深化。当然推进思维深化的方式有多种，可以是由果到因的追根溯源，也可以是由因到果的推演判断，还可以是通过对比归纳后的总结。总之，我们要让学生在数学学习中透过现象，逐层深入，抓住本质。

比如在教学《分数的初步认识》时，在学生初步学习了几分之一后，安排了这样两个层次的动手操作活动：

活动一：折出一张正方形纸的四分之一。

学生折完，展示各种折法。

追问：为什么折的方法不一样，但都能用四分之一这个分数来表示呢？学生思考后明白，不管怎样折，只要是把正方形纸平均分成四份，每一份就都可以用四分之一来表示。

活动二：准备圆、长方形、正方形等不同形状的图形，让学生折出每种图形的四分之一。

学生折完，展示。

追问：为什么不同形状的图形，它们的阴影部分都可以用四分之一来表示呢？

学生交流，思考后明白：无论什么图形，只要平均分成四份，其中的一份就可以用四分之一来表示。

通过两次追问，学生对“平均分”和“几分之一”的数学概念的认识变得更真切、准确和完整，同时也理解了概念的本质，提升了思维水平。

总之，及时有效的追问，能够让学生透过表面现象，理解数学知识的本质、还原学生真实的思考过程。在课堂上，当老师的“追问”成为一种习惯时，学生的思考也自然成为一种习惯，这样良性循环，学生思维的深度和广度会不断发展，学生数学思维能力的提升也就成了有本之木，有源之水。