超混沌数字电路在数字供应链中的应用

李玥++张之光

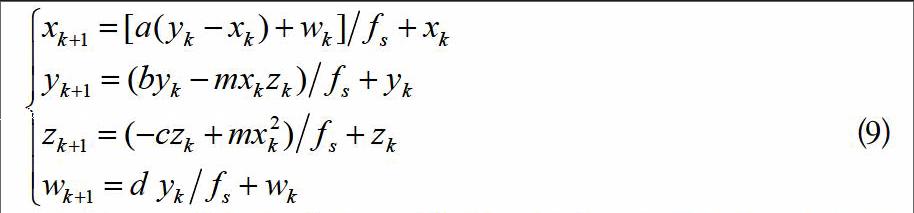
摘要：随着网络技术的迅猛发展和用户创造内容（UGC）的网络数字信息资料指数倍增长，数字供应链管理已然成为一个新的热点。本文以超混沌系统为研究对象，采用优化的一阶数字差分方程将混沌系统进行预处理，提出了基于DSP Builder超混沌数字电路设计方案。该數字电路可通过FPGA进行快速开发，通过相应的软件平台支撑，可以直接运用于数字供应链中，提升信息的安全性和保密性。

关键词：超混沌数字电路 数字供应链 超混沌系统

中图分类号：TN79 文献标识码：A 文章编号：1007-9416（2016）12-0078-02

混沌系统由于对初值、参数的敏感性，轨迹的伪随机性、不可预测性和遍历性，在保密信息中有广泛运用前景。本文尝试将数字混沌系统引入数据量巨大的云环境数字供应链的传输调制端，通过优化电路设计，在一定精度下避免其动力学退化的问题。

1 系统的动力学行为研究

1.1 系统的扩展

经典系统是一个典型三维自治非线性系统，可表述为：

上式中常数为控制参数，状态变量有。当系统参数时，系统处于混沌状态。

将系统从维度增加一并获取反馈至，可以获得四维系统。

上式中常数为系统参量。

1.2 四维系统性能分析

（2）式中的四维系统是一个耗散系统散度为：

当，且时，初始体积的体积元在时间时收缩为体积元，即一个吸引子上。

四维系统的矩阵为：

可见该四维系统具有唯一的平衡点，平衡点处的特征值为。平衡点是不稳定的鞍结点。

从解可以看出，该四维系统正Lyapunov指数有两个，系统处于超混沌状态其Lyapunov维数为公式

由解可看出，Lyapunov维数是分数，说明该系统属于超混沌系统的范畴。

2 数字混沌信号的生成规则

2.1 超混沌系统的离散化

混沌系统的时域波形具有非周期性，可以通过低通滤波等简单方法提取。将图1三维Lorenz系统进行快速傅里叶变换，根据变换结果归一化处理，得出带宽比较图如图1所示。

从图1中可以看出，三维Lorenz系统带宽较超系统带宽窄。

2.2 离散仿真算法的不足

离散化混沌系统采用式（7）的快速数字差分算法：

其中为采样时间，将其变形可得：

上式中为采样频率。由于这类系统采样频率较低（仅为100Hz），精度有限，故相空间出现了锯齿状轨迹。

2.3 优化的一阶离散化方程

采用一阶差分公式（7）将超混沌系统（2）的微分方程组离散化，迭代规则如下：

在（9）式中采样频率能同时作用于混沌系统的线性项和非线性项。

3 超混沌系统的数字电路设计（如图2）

本数字混沌系统的采样频率为增益模块Gain（fs）取值的倒数。此时的采样频率取值为1000Hz，设定初值为（0，1，1，0）。本电路构成一个数字积分反馈网络，将x， y， z， w信号反馈到数据选择器。

4 超混沌数字电路实验结果

在通过实验将混沌时间序列各向量在数字电路示波器中显示，如图3所示。从该实验结果上看，各向量时间序列具备较好的混沌属性，能够运用于混沌的调制或加密。

在采样频率过低的条件下，不能获得超混沌，没有可控的收敛信号轨迹，没有得到超混沌吸引子相图，故没有得到理想的实验结果。如图4所示。

在采样频率取值为1000Hz时，从各平面相图5看出，实验结果比较理想，各吸引子的形状、幅值

都。

通过实验可以看出，虽然理论推断上，更高的采样频率能反映超混沌系统的动力学特性，取得越大，离散化后的系统就越能精确反映原系统的动态特性，在采样频率取值为1000Hz时获得的实验结果最为理想，也最具实用价值。这与本文第二章论证的数字混沌信号生成规则是相吻合的。

5 结语

本文基于现代数字信号处理技术，在数字供应链的应用环境中，通过优化的离散化方程改进了数字电路，设计实现了超混沌系统族的数字电路。设计的数字电路在实际应用中可以通过通过增益模块和常数模块的调整实现混沌系统的参数配置而改变超混沌的离散特性，可移植性较好。实验结果较为理想，电路运行得到的相图与Matlab模拟仿真相近。

参考文献

[1]Lorenz Edward Norton.Deterministic nonperiodic flow[J].Journal of Atomsphere Science. 1963，20：130-141.

[2]王兴元，王明军.三种方法实现超混沌Chen系统的反同步[J].物理学报，2007，56（12）：6843-6850.

[3]Ge Zhengming， Cheng-Hsiung Yang. Chaos synchronization and chaotization of complex chaotic systems in series form by optimal control[J].Chaos， Solitons and Fractals，2009，42：994-1002.