基于单值中智集VIKOR的应急群体决策方法*
谭睿璞,张文德,陈龙龙
(1. 福州大学 经济与管理学院,福建 福州 350116;2. 福建江夏学院 电子信息科学学院,福建 福州 350108;3. 福州大学 信息管理研究所,福建 福州 350116;4. 福州大学 信息化建设办公室,福建 福州 350116)
0 引言
近年来,我国社会经济建设的快速发展创造了大量财富,但同时带来的系列其它社会与经济问题也应运而生,其中1个十分重要的方面就是各种突发事件频发。如:2014年12月,上海外滩跨年夜活动,发生踩踏事件,造成36人死亡,49人受伤[1];2015年,河南省平顶山市鲁山县1家名为康乐园的民办老年公寓发生火灾,造成38人死亡;2016年6月,全国14省(区、市)遭遇暴雨,造成全国1.37亿人次受灾,1 074人死亡,624万人次紧急转移安置,40万间房屋倒塌,直接经济损失2 983亿元[2]。总之,突发事件无论从发生频率、规模及复杂性程度上都呈上升趋势,给人民和国家造成巨大的人员伤亡和财产损失。突发事件一般具有复杂性、扩散性和高破坏性等特点, 如何根据突发事件的特征进行及时、有效决策,具有重要的理论意义和现实作用。因此,近几年来应急决策方法成为研究热点[3-11]。Zhao等[7]提出基于模糊AHP和WOWA算子的决策方法,并应用于无人值守运行的地铁系统急救方案评价;Wang等[8]提出考虑区间动态参考点法的、基于前景理论的应急决策方法;Xu等[9]提出基于群体偏好一致性和广义区间梯形模糊数的应急群体决策方法;Zhang等[10]提出区间值模糊环境下的不确定网络舆情应急决策方法;Sun等[11]提出基于软模糊粗糙集的非常规突发事件应急预案评价方法。
由于实际应急决策环境的复杂性和不确定性,决策信息通常具有模糊、犹豫和不确定性的特点,很难给出精确的数据[3]。因此,近年来决策信息常表征为模糊数、直觉模糊数等模糊信息,而1999年Smarandache[12]提出中智集能够满足这种决策需求。中智集更接近于人的思维,体现由于不完整知识、知识获取的过失或随机猜测而造成的不确定性的特点。中智集是元素的真实程度(T)、不确定程度(I)及谬误程度(F)存在于非标准单位区间的集合,是对模糊集、直觉模糊集及悖论集合等的概括总结。为便于将中智集应用于实际问题中,Wang等[13-14]提出区间中智集(INS)和单值中智集(SNS)的概念;王坚强等[15]提出多值中智集概念,并将其应用于多属性决策;Ye[16]提出基于梯形中智的决策方法。然而,综合国内外文献研究成果,将中智集应用于突发事件应急决策还较少见,因此提出基于单值中智集的拓展VIKOR应急群决策方法。
1 基础理论
1.1 中智集和单值中智集
定义1[13]设X为对象集,x为其中任意1个元素,X上的1个中智集A可以由真实程度函数TA(x),不确定程度函数IA(x)及谬误程度函数FA(x)表示,其中TA(x),IA(x)和FA(x)是]0-,1+[ 的标准或非标准实数子集,即TA(x):X→]0-,1+[,IA(x):X→]0-,1+[,FA(x):X→]0-,1+[(其中非标准有限数1+=1+ε,“1”是它的标准部分,“ε>0”为无穷小数,是它的非标准部分),且0-≤supTA(x)+supIA(x)+supFA(x)≤3+。
定义2[14]设X为对象集,x为其中任意1个元素,X上的1个单值中智集A可以由真实程度函数TA(x),不确定程度函数IA(x)及谬误程度函数FA(x)表示:
A={
其中:TA(x),IA(x),FA(x)∈[0,1],并满足0≤TA(x)+IA(x)+FA(x)≤3。为简便起见,1个单值中智数可以表示为a={T,I,F}。
定义3[17]设a1={T1,I1,F1}和a2={T2,I2,F2}是2个单值中智数,则
1)λa1=<1-(1-T1)λ,(I1)λ,(F1)λ>;λ>0。

3)a1⊕a2=
4)a1⊗a2=
定义4[18]设a1={T1,I1,F1}和a2={T2,I2,F2}是2个单值中智数,则其标准化的Euclidean距离为:
D(a1,a2)=
(1)
定义5[18]设a1={T1,I1,F1}是1个单值中智数,则其模糊性测度定义如下:
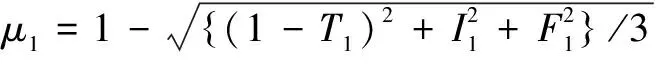
(2)
1.2 中智熵
针对指标权重未知的决策问题,基于李鹏等[19]提出的直觉模糊熵确定属性权重的方法,提出基于中智熵的属性权重确定方法。
定义6 设X=(x1,x2,…xn),单值中智集A={
(3)
在单值中智决策矩阵F(aij) (其中aij表示第i个方案的第j个属性)中,对任意1个属性,根据式(3)可以计算出其中智熵。熵表示属性值的不确定,熵越大、不确定性越大,则权重可由式(4)计算得出:
(4)
2 基于单值中智集VIKOR方法的应急决策模型
VIKOR方法是由Opricovic等人提出的1种基于理想法的折中排序方法,通过最大化群体效用和最小化个体遗憾,实现对有限决策方案的优选排序[21]。将传统VIKOR方法扩展到单值中智数环境下,为应急决策提供1个科学合理的决策框架。
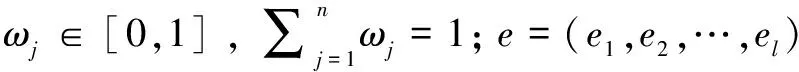
步骤1:确定专家权重。根据给定语言术语评价值及相对应的单值中智数表征的决策专家重要性,根据公式(2)可得专家权重如下[18]:

(5)
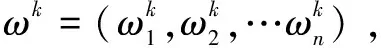


(6)
步骤 4:确定单值中智数正理想解方案A+和负理想方案A-,其中:
{(1,0,0),(1,0,0),…,(1,0,0)},
{(0,1,1),(0,1,1),…,(0,1,1)}。
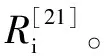
(7)
(8)
步骤 6:综合考虑群体效用值Si和个体遗憾值Ri的基础上,获取各应急方案的折中评价值[21]。
(9)
式中:S+= minSi,S-= maxSi,R+= minRi,R-= maxRi。λ∈[0,1]为最大群体效用权重或决策机制系数,如果λ=0.5,则表示根据均衡折中的方式进行决策,在VIKOR中,一般选取λ=0.5。
步骤 7:按照Qi,Si,Ri数值大小进行升序排序,得到3个排序序列Qσ,Sσ,Rσ。
步骤 8:确定妥协解。
1) 若x(1)是Qσ中排在第1的应急方案,如果它同时满足下面2个判断条件,则被视为最佳折中决策结果。条件1:可接受优势准则Q(x(2)) -Q(x(1)) ≥ 1/(m-1),式中x(1),x(2)分别表示序列Qσ中排在第1、第2的最优决策结果,m是方案的总数目,并且有m≤4时,取1/(m-1)=1/4[21];条件2:可接受稳定性准则,如果x(1)在序列Sσ,Rσ中也是排在第1位,则x(1)在决策过程中是稳定的。
2)如果上述2个条件有1个不满足,则得到1组妥协解。如果仅仅不满足可接受稳定准则,x(1),x(2)都为最优决策结果;如果不满足可接受优势准则,由Q(x(U)) -Q(x(1)) < 1/(m-1)可得到最大U值,则x(1),x(2),…,x(U)在Qσ中是临近排序,都接近理想方案。
3 实例分析
3.1 算例分析
应急决策问题是现代社会背景下的热点问题,尤其是复杂的群体应急决策问题更值得关注和研究。在对文献[23]中应急决策问题数据进一步丰富和完善的基础上,解决事发后确定当前最佳救援点的应急决策问题。以某次交通突发事件为例,针对3 个应急救援点(x1,x2,x3),由4 名专家构成决策群体,救援点的评判指标有:出行能力(c1)、储备能力(c2)、调度能力(c3)、后勤保障能力(c4)。专家对3 个救援点(方案)的4个属性进行评价,指标评价值采用单值中智数表示。为适应应急决策的环境,同时考虑现实中人类倾向于用定性的语言信息来评价属性,采用文献[18]给出的语言术语和单值中智集的对应关系表给定评价数据,如表1所示,则基于表1中专家的重要性评价及对应急方案的评价,如表2~6所示。

表1 语言术语与单值中智数对应关系

表2 专家重要性评价

表3 专家1的单值中智数决策矩阵

表4 专家2的单值中智数决策矩阵

表5 专家3的单值中智数决策矩阵

表6 专家4的单值中智数决策矩阵
1)确定专家权重。利用表1、表2及公式(5),可得专家权重为:
e=(e1,e2,e3,e4)=(0.288,0.288,0.212,0.212)
2)利用中智熵求出属性权重。利用公式(3)和公式(4),可得属性权重为:
ω=(0.256,0.233,0.195,0.315)



4)利用式(7)、式(8)和式(9),可得群体效用值Si、个体遗憾值Ri和折中评价值Qi为:

表7 各方案群体效用值、个体遗憾值和折中评价值
由表7可知,根据折中评价值Qi的大小得到应急决策方案的优先序为x1≻x2≻x3,因此最优方案为x1,即第1个救援点为此次最佳救援点。方案x1在Si中排名也为第1,说明满足可接受稳定性准则。同时由于Q(x(2))-Q(x(1))=0.500-0.099=0.401≥0.25,说明满足可接受优势准则。
3.2 灵敏度分析
在VIKOR方法中,各应急方案的折中评价值受最大群体效用权重或决策机制系数λ的影响,为考虑λ取值不同时对评价决策结果的影响,通过设置不同的λ值进行灵敏度分析,观察其对基于Qi的排序结果的影响,具体如图1所示。
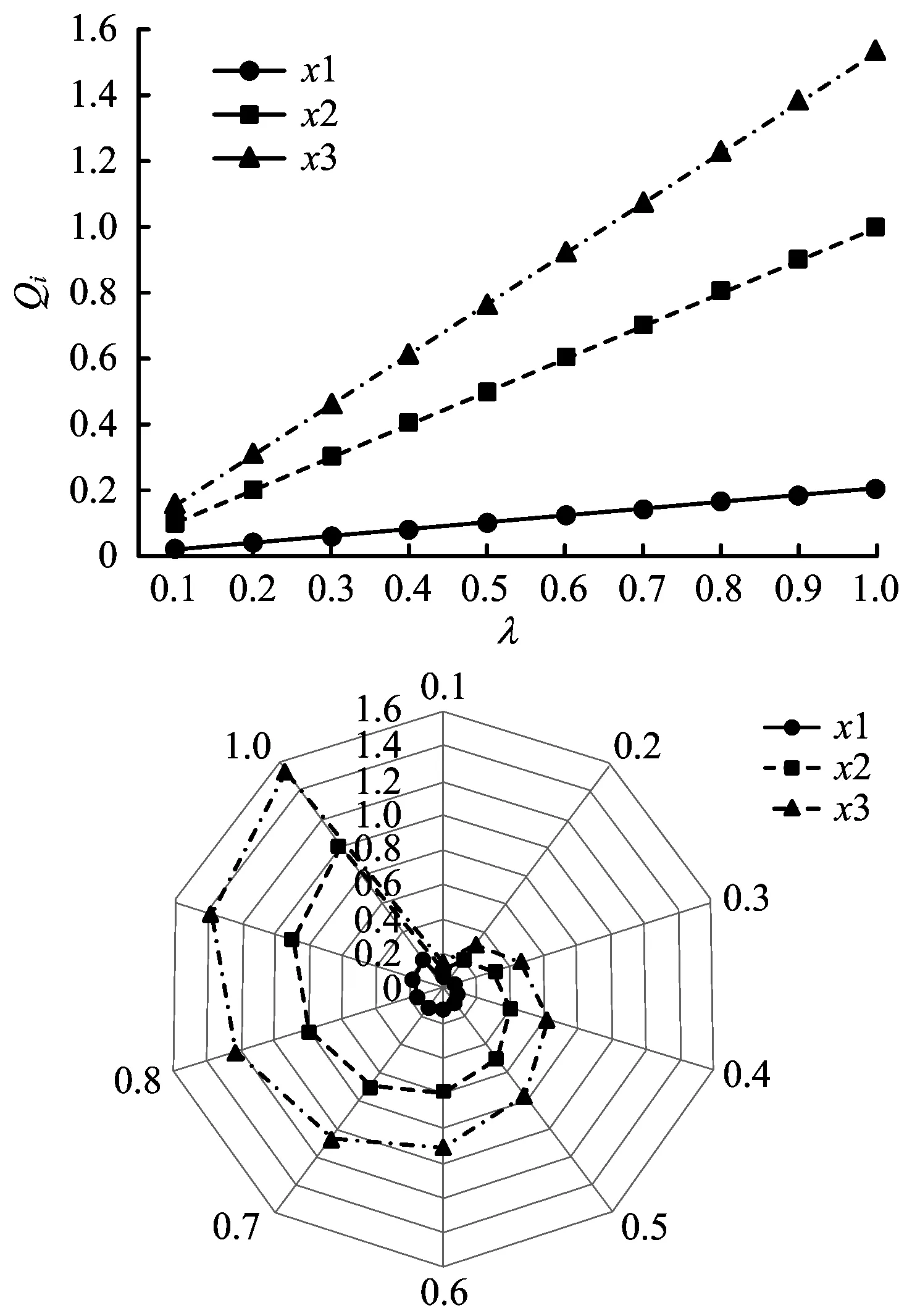
图1 灵敏度分析结果Fig.1 Sensitivity analysis results
从图1可知,在不同的λ取值下,应急方案排序结果具有稳定性,最优方案保持不变,λ对排序结果影响有限。
3.3 与TOPSIS 法对比分析

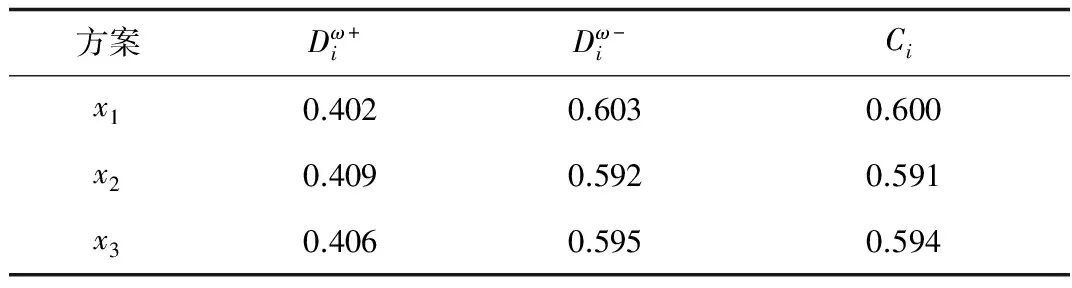
表8 TOPSIS方法计算结果
根据Ci值的大小,应急决策方案的有限排序为x1≻x3≻x2,最优方案为x1,与VIKOR方法的最优方案一致,从而验证方法的有效性。另外采用TOPSIS方法得出的相对贴近度值Ci都很接近,特别是方案x2和x3,而VIKOR方法的折中评价值的区分度更高,能够更显著的区分各应急方案。
4 结论
1)针对突发事件应急决策问题,提出1种基于单值中智数的扩展VIKOR应急群决策方法。
2)提出基于中智信息熵的属性权重计算方法,同时利用单值中智数模糊性测度计算专家权重,解决决策过程中权重未知的问题。
3)将VIKOR方法扩展到单值中智数环境下,并通过应急突发事件算例分析、灵敏度分析及与TOPSIS方法的对比分析,验证方法的有效性和合理性。
4)对基于中智集(单值中智集、区间中智集、梯形中智模糊数、双极中智集及中智图)的决策方法及在应急决策问题中的应用进一步深入研究,是未来研究的重点。
[1]光明新闻. 12·31上海外滩踩踏事故[EB/OL]. (2015-01-13)[2016-11-15]. http://news.gmw.cn/newspaper/2015-01/13/content_103695455.htm.
[2]新华网. 今年14省份遭洪涝灾害 死亡79人经济损失137亿元[EB/OL]. (2016-06-04)[2016-11-15]. http://news.xin huanet.com/politics/2016-06/04/c_129039939.htm.
[3]郑晶, 王应明, 陈圣群. 考虑方案有效性的应急案例决策方法[J]. 控制与决策, 2016, 31(10): 1824-1830.
ZHENG Jing, WANG Yingming, CHEN Shengqun. Decision method for emergency case with considering effectiveness of alternative [J]. Control and Decision, 2016, 31(10): 1824-1830.
[4]赵树平, 梁昌勇, 罗大伟. 基于诱导型直觉不确定语言集成算的应急预案评估群决策方法[J]. 计算机应用研究. 2016, 33(3):726-729.
ZHAO Shuping, LIANG Changyong, LUO Dawei. Emergency plan evaluation group decision making method based on induced intuitionistic uncertain linguistic aggregation operators [J]. Application Research of Computers, 2016, 33(3):726-729.
[5]陕振沛, 张转周, 宁宝权. 基于直觉模糊集TOPSIS决策方法的应急预案综合评价研究[J]. 数学的实践与认识, 2016(3):160-166.
SHAN Zhenpei, ZHANG Zhuanzhou, NING Baoquan. The application of intuitionistic fuzzy sets in evaluating emergency response plan using TOPSIS method [J]. Mathematics in Practice and Theory, 2016 (3):160-166.
[6]徐选华, 蔡晨光, 王佩, 等. 面向具有多部门多指标特征的复杂大群体应急决策方法[J]. 控制与决策, 2016, 31(2):225-232.
XU Xuanhua, CAI Chenguang, WANG Pei,et al. Complex large group emergency decision making method orientedcharacteristic of multi-department and multi-index [J]. Control and Decision, 2016, 31(2):225-232.
[7]Zhao B, Tang T, Ning B. Applying Hybrid Decision-Making Method Based on Fuzzy AHP-WOWA Operator for Emergency Alternative Evaluation of Unattended Train Operation Metro System[J]. Mathematical Problems in Engineering, 2016, 2016(2-4):1-12.
[8]Wang L, Zhang Z X, Wang Y M. A prospect theory-based interval dynamic reference point method for emergency decision making[J]. Expert Systems with Applications, 2015, 42(23):9379-9388.
[9]Xu X, Cai C, Chen X, et al. A multi-attribute large group emergency decision making method based on group preference consistency of generalized interval-valued trapezoidal fuzzy numbers[J]. Journal of Systems Science & Systems Engineering, 2015, 24(2):211-228.
[10]Zhang Q S, Xie B L, Zhang X M. Uncertain internet public opinion emergency decision-making method under interval-valued fuzzy environment[J]. Applied Mechanics & Materials, 2015, 713-715:2024-2028.
[11]Sun B, Ma W. An approach to evaluation of emergency plans for unconventional emergency events based on soft fuzzy rough set[J]. Kybernetes, 2016, 45(3):461-473.
[12]Smarandache F. A Unifying Field in Logics: Neutrosophy, Neutrosophic Probability, Set and Logic [M]. Rehoboth: American Research Press, 1999.
[13]Wang H, Smarandache F, Zhang Y Q et al. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing [M]. Hexis: Arizona, 2005:6-14.
[14]Wang H B. Smarandache F, Zhang Y Q, et al. Single valued neutrosophic sets [J]. Multispace and Multistructure, 2010, 4(10):410-413.
[15]王坚强, 李新娥. 基于多值中智集的TODIM方法[J]. 控制与决策, 2015,30(6):1139-1142.
WANG Jianqiang, LI xine. TODIM method with multi-valued neutrosophic sets [J]. Control and Decision, 2015, 30(6):1139-1142.
[16]Ye J. Trapezoidal neutrosophic set and its application to multiple attribute decision-making[J]. Neural Computing and Applications, 2015, 26(5):1157-1166.
[17]Peng J J, Wang J Q, Zhang H Y, et al. An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets[J]. Applied Soft Computing, 2014, 25(25):336-346.
[18]Biswas P, Pramanik S, Giri B C. TOPSIS method for multi-attribute group decision-making under single-valued neutrosophic environment[J]. Neural Computing and Applications, 2016, 27(3):727-737.
[19]李鹏, 吴君民, 朱建军. 基于新直觉模糊距离的随机决策方法[J]. 系统工程理论与实践, 2014,34(6):1517-1524.
LI Peng, WU Junmin, ZHU Jianjun. Stochastic multi-criteria decision making methods based on new intuitionistic fuzzy distance [J]. Systems Engineering-Theory & Practice, 2014, 34(6): 1517- 1524.
[20]Majumdar P, Samanta S K. On similarity and entropy of neutrosophic sets[J]. Journal of Intelligent & Fuzzy Systems Applications in Engineering & Technology, 2014, 26(3):1245-1252.
[21]杨山亮, 王鹏, 李革,等. 基于直觉模糊VIKOR方法的装备优选群决策模型[J]. 系统仿真学报, 2015, 27(9):2169-2175.
YANG Shanliang, WANG Peng, LI Ge, et al. Group decision making model for weapon selection using extended VIKOR method under intuitionistic fuzzy environment [J]. Journal of System Simulation, 2015, 27(9):2169-2175.
[22]Ye J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets[J]. Journal of Intelligent & Fuzzy Systems Applications in Engineering & Technology, 2014, 26(5):2459-2466.
[23]王畅, 曾亚. 基于直觉模糊集的应急决策方法研究[J]. 情报探索, 2016(3):125-128.
WANG Chang,ZENG Ya. Study on intuitionistic fuzzy set-based emergency decision making method [J]. Information Research, 2016 (3):125-128.

