隧道并行输气管道爆炸对邻管的冲击效应分析*
文 霞,姚安林,2,陈 谦,徐涛龙,2
(1.西南石油大学 石油与天然气工程学院,四川 成都 610500;2.油气消防四川省重点实验室,四川 成都 610500; 3.中石油天然气销售东部分公司,上海 200122)
0 引言
近年来,随着我国输气管道建设速度的加快,输气管道采用管隧并行敷设方式通过各种障碍点的情况日益增多。例如,中卫—贵阳输气管道通过秦岭和大娄山区,与西气东输二线、兰成原油管道、兰成渝成品油管道、中缅原油管道并行敷设,其中,与兰成原油管道共用40座隧道,全长约42.99 km[1];陕京三线输气管道总长约1 026 km,与石楼—顺义成品油管道共用隧道[2];中缅油气管道(国内段)工程隧道穿越共64处,天然气、原油、成品油三管同隧河流大型穿跨越14处[3];西气东输二线管道工程果子沟隧道内同时敷设2根D1219 mm×26.4 mm管道,是西气东输二线西段管道工程重要控制性工程之一[4]。由于隧道内的输气管道具有所处环境敏感、致灾因素复杂和事故抢修困难等特点,管道不仅要克服自身输送介质易燃易爆的脆弱性,还需防范来自邻近管道失效所引起的连锁破坏。因此,有必要针对隧道并行管道爆炸对邻管的力学影响和冲击破坏进行研究。
随着数值模拟方法的广泛应用,出现了多种分析算法,如拉格朗日(Lagrange)法、欧拉(Euler)法、CLE(Couple Lagrange Euler)法[5]和ALE(Arbitrary Lagrange Eule)法[6]。目前,隧道、管道、空气和炸药等多种物质共存的爆炸模拟主要采用ALE算法。众多国内外学者就爆炸荷载对管道的影响进行了大量研究[7-10]。以下在已有研究的基础上拟合出气体泄漏扩散分布,利用TNT当量法计算出等效炸药尺寸。建立了隧道、管道、空气和炸药的多物质耦合模型,得到管道在不同的泄漏尺寸、爆心距和风速(共15种工况)下的爆炸冲击动力响应。
1 天然气泄漏的TNT当量
当管内介质压力较高时,孔口为临界流泄漏,气体泄漏率[11]的计算公式如下:
(1)
式中:Q为气体泄漏率,kg/s;A为泄漏孔面积,m2;CD为泄漏系数,取1.0(圆形孔);k为气体绝热系数;P1为泄漏起点的压力,Pa;T1为泄漏起点的温度,K;M为气体摩尔质量,kg/mol;R为气体常数,取8.314 J/(mol·K);φ为孔口流速系数。
天然气爆炸的浓度下限为5.3%,泄漏扩散浓度大于5.3%的蒸气云分布[12]为:

(2)
式中:x,y和z分别为下风向、横风向和垂直风向扩散长度,m;u为风速,m/s。
基于TNT当量法,利用TNT爆炸的破坏作用代替蒸气云爆炸的破坏作用,能较准确、方便地分析出爆炸的危害,TNT当量的计算[13]见式(3)。
(3)
式中:WTNT为TNT当量,kg;λ为蒸气云爆炸当量系数;W为参与爆炸的蒸气质量,kg;Q为蒸气燃烧热,MJ/kg;QTNT为TNT的爆炸热,MJ/kg。
由以上分析可得,TNT当量与风速、泄漏率的关系分别见图1和图2。
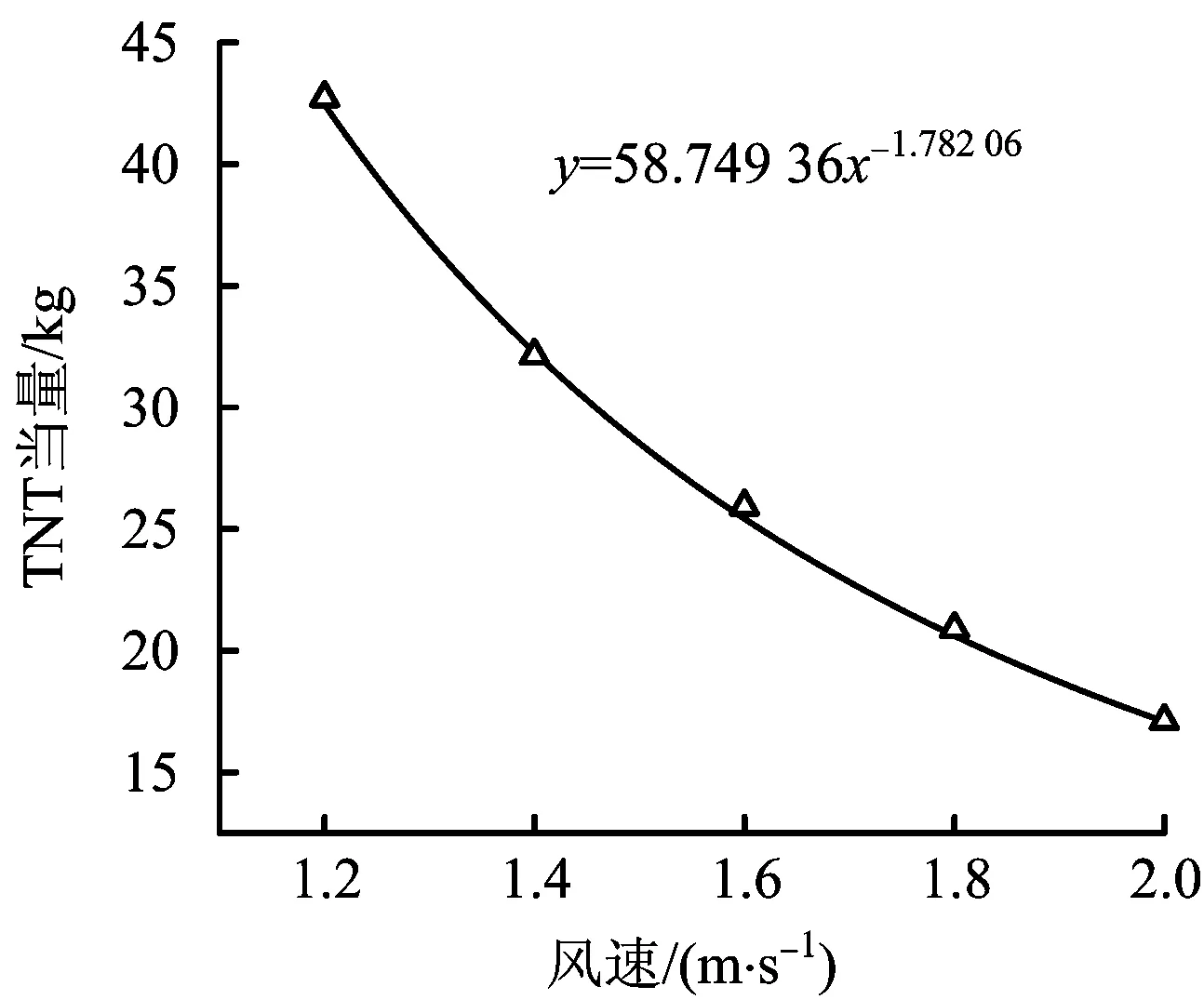
图1 TNT当量与风速关系Fig.1 Relationship between TNT equivalent and wind speed
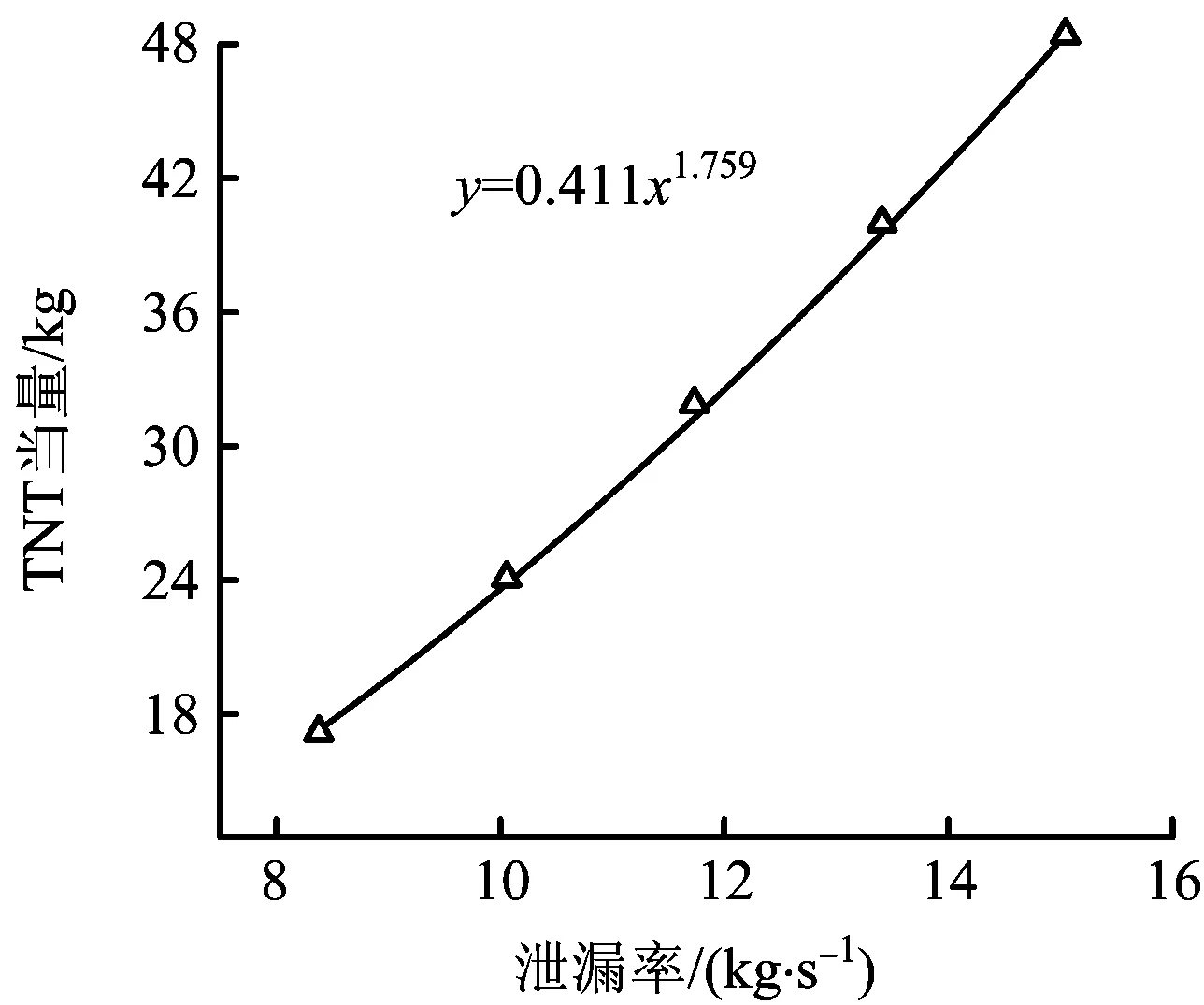
图2 TNT当量与泄漏率关系Fig.2 Relationship between TNT equivalent and leakage rate
2 管隧并行输气管道爆炸响应分析
2.1 有限元建模
根据图3所示的某管隧的实际几何尺寸,建立有限元分析模型。圆形虚线指爆炸前的管道,虚线内的矩形指将爆炸蒸气云等效成条状的炸药。由于管隧结构的对称性,选用1/2管隧模型,隧道模型长5.0 m,断面净高4.3 m,其中,直墙高2.05 m,拱高2.25 m,内径为4.5 m,衬砌厚度为300 mm,隧道内并行架空敷设输气管道,管径为1 016 mm,壁厚为26.2 mm,管材为X70,管道中心离隧道底部1 025 mm。细化管道、炸药及周围空气单元的网格边长至100 mm,管道周围空气单元的尺寸比例设置为5,其余单元的网格边长为400 mm,有限元网格划分如图4所示。

图3 管隧断面Fig.3 Section of pipeline and tunnel
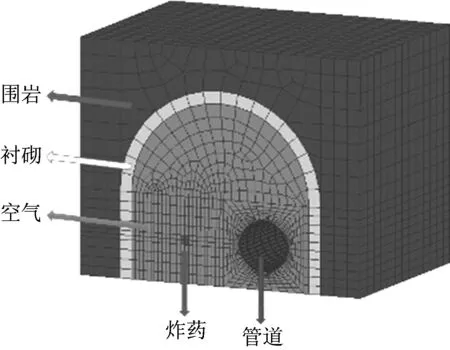
图4 模型网格划分结果Fig.4 Result of model grid
空气和炸药采用Euler单元,围岩、衬砌和管道采用Lagrange单元,有限元分析采用Soild164八节点六面体单元。设定炸药与空气为多物质组,衬砌与围岩采用面面接触,空气与管道、衬砌分别进行流固耦合分析。将图4显示的隧道前断面设置为对称约束,其余面为无反射约束。
2.2 材料选取
炸药的模拟常选用*MAT_HIGH_EXPLOSIVE_BURN材料和JWL状态方程。炸药爆轰产物的状态方程式为
(4)
式中:V为相对体积;E0为初始内能密度,J/m3;E0为7.0×109J/m3;A为371.2 GPa;B为3.231 GPa;R1为4.15;R2为0.95;ω为0.35;选取炸药密度为1.63 g/cm3,爆速为6 700 m/s,爆压为28 GPa。
管道采用Johnson-Cook材料模型和Gruneison状态方程进行模拟。
压缩材料压力:
p1=
(γ0+αμ)E
(5)
膨胀材料压力:
p2=ρ0c2μ+(γ0+αμ)E
(6)
式中:ρ为材料密度,取7.85 g/cm3;ρ0为初始密度,g/cm3;μ为体积变化率,μ=ρ/ρ0-1;c=4 569 m/s;S1=1.49;S2=S3=0;γ0=2.17;α=0.46[14]。
空气的模拟采用*MAT_NULL空材料模型和*EOS_LINEAR_POLYNOMIAL状态方程。其状态方程式为
P=c0+c1μ+c2μ2+c3μ3+(c4+c5μ+c6μ2)ρ0E
(7)
式中:ρ0为气体的初始密度,g/cm3;E0为单位体积初始内能,J/cm3;V为相对体积,μ=1/V-1;ci(i=0,1,2,3,4,5,6)为常数;ρ0为1.292 9×10-3g/cm3;E0为2.5 J/cm3;c0为1.0×10-6;c4和c5为0.5;V0为1.0。
隧道衬砌材料为C25,采用*MAT_JOHNSON_HOLMQUIST_CONCRETE混凝土模型模拟。JHC模型的本构方程是:
(8)
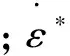
JHC本构参数取值:密度为2.4 g/cm3;剪切模量为14.86 GPa;应变率系数为0.007;压溃压力为16.7 MPa;失效应变为0.02。
围岩材料选择*MAT_PLASTIC_KINEMATIC材料模型。材料参数取值:混凝土密度2.65 g/cm3;弹性模量为65 GPa;泊松比为0.24;屈服应力为0.1 GPa;切线模量为4.0 GPa;β为0.5;失效应变为0.8。
3 结果分析
为了掌握隧道内输气管道泄漏后爆炸对相邻管道的动力响应规律,利用LS-DYNA有限元软件对不同泄漏尺寸、爆炸距离和风速下的15种工况进行模拟计算。基于式(2)所示的蒸气云分布,利用MATLAB拟合出泄漏气体爆炸的总扩散体积;由式(3)所示的TNT当量计算法,得到等效的炸药尺寸,具体结果见表1。
3.1 模型验证
为了说明数值模拟的可靠性,将得到的数值模拟结果与经验公式计算结果进行对比。管道在爆炸荷载作用下的峰值振速可用萨道夫斯基经验公式[15]计算,见式(9)。

(9)
式中:vmax为峰值振速,m/s;K为爆炸场地系数;W为装药量,kg;R为爆心距,m;η为衰减系数。
根据数值模拟结果,可得到管道峰值振速与泄漏孔口面积的关系。由表1可知,A组数据的5种泄漏孔口面积对应于5种不同的TNT当量。因此,可拟合出与式(9)类似的管道峰值振速与TNT当量的关系,其中,K取2.635 7,η取3.473 4,见式(10)和图5。
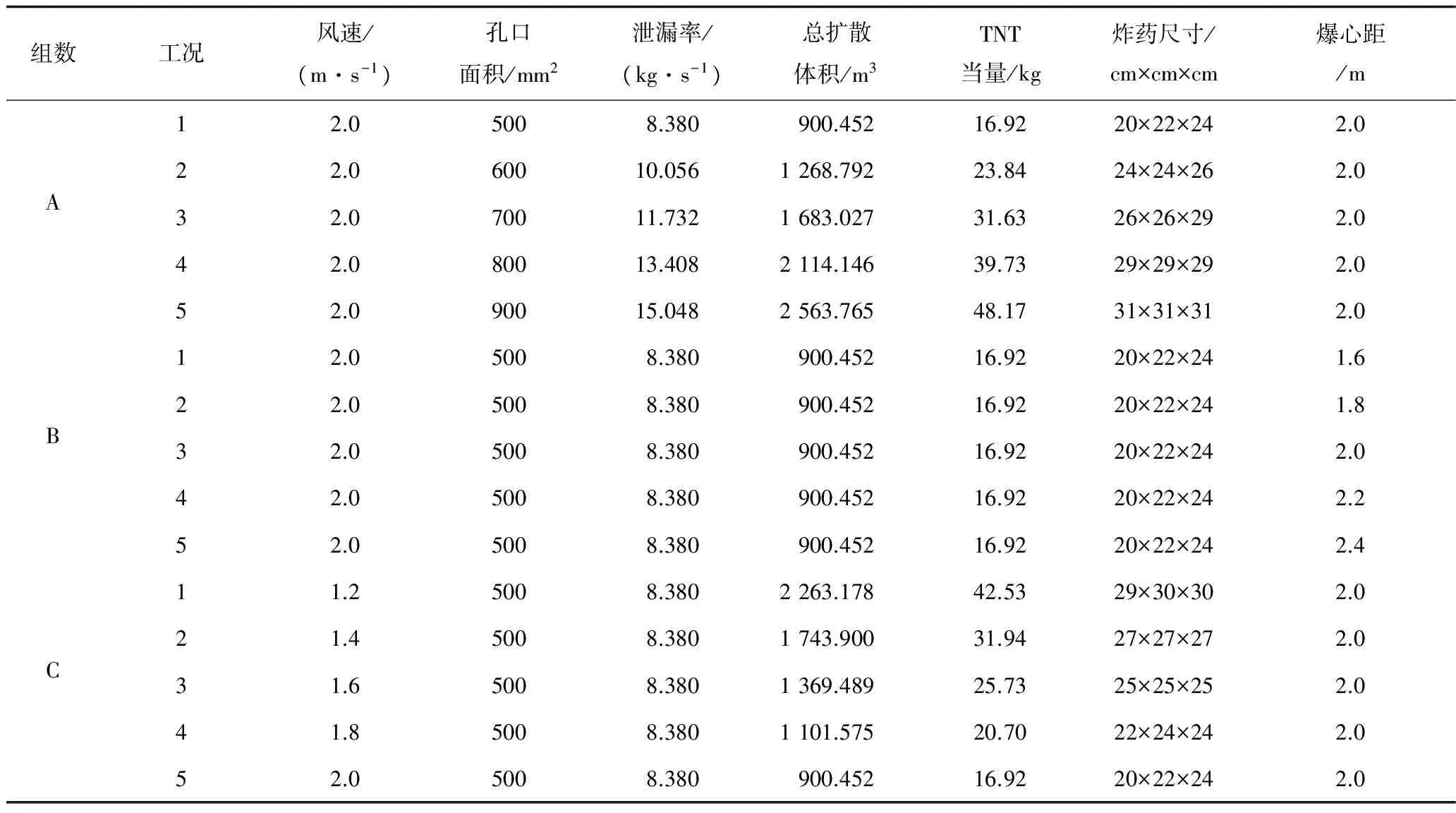
表1 各种工况对应的参数值
(10)
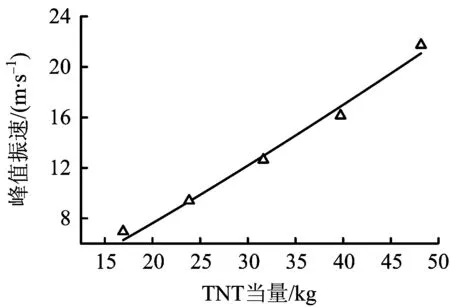
图5 峰值振速与TNT当量关系Fig.5 Relationship between peak velocity and TNT equivalent
由图5和式(9)可得,当TNT当量为16.92 kg时,管道的峰值振速与爆心距R的关系式为:
vmax=69.684 8R-3.473 4
(11)
将表1中B组数据模拟的结果和经验式(11)计算的结果进行对比,绘制于图6中。
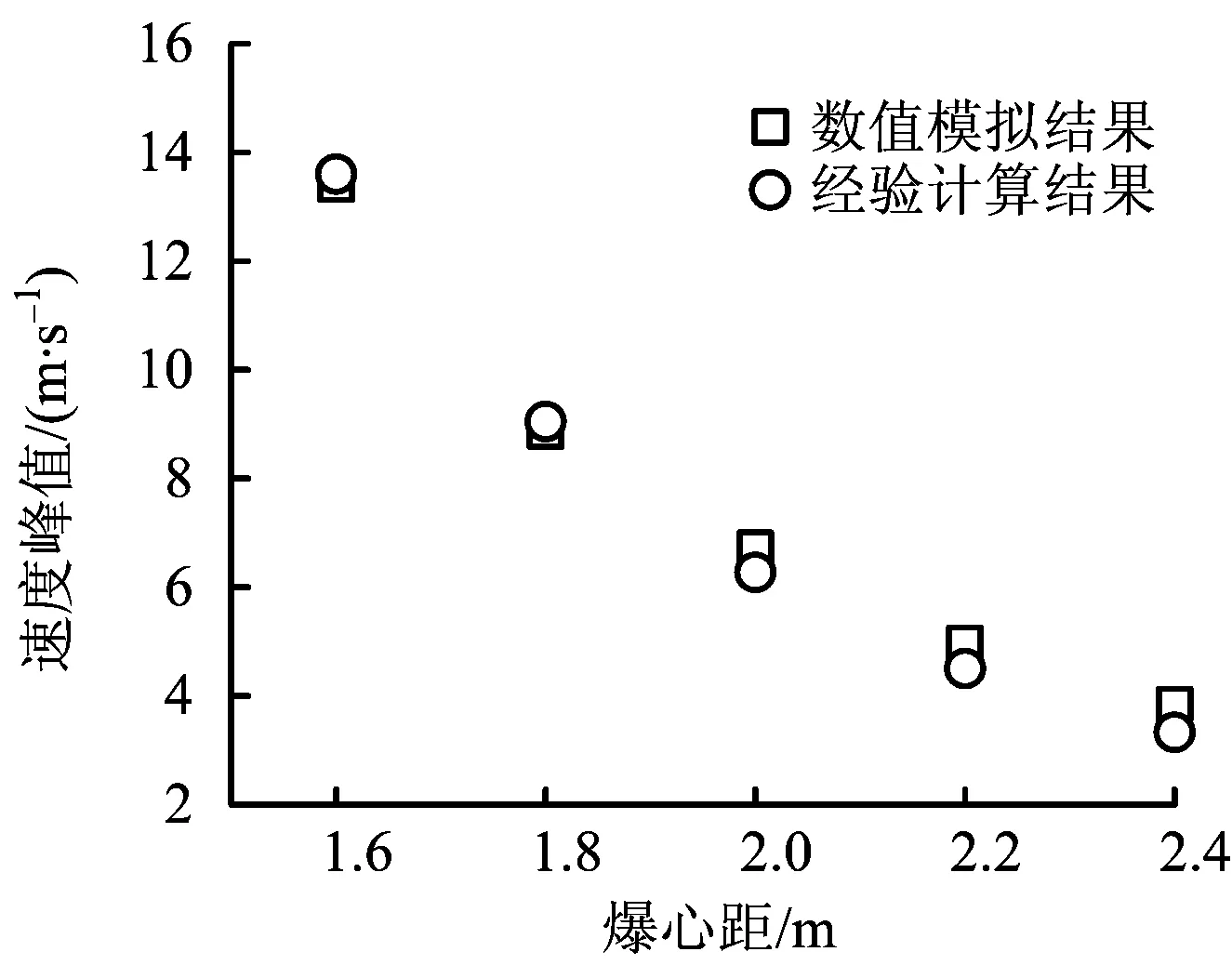
图6 结果对比Fig.6 Comparison of results
如图6所示,数值模拟结果和经验计算结果比较接近,说明采用该模型模拟隧道内管道的爆炸影响规律是可行的。
3.2 不同泄漏尺寸
选取表1中的A组数据,模拟与爆心最近的管道单元在不同泄漏尺寸下的动力响应,见图7~图9。

图7 等效应力时程Fig.7 Time history of effective stress
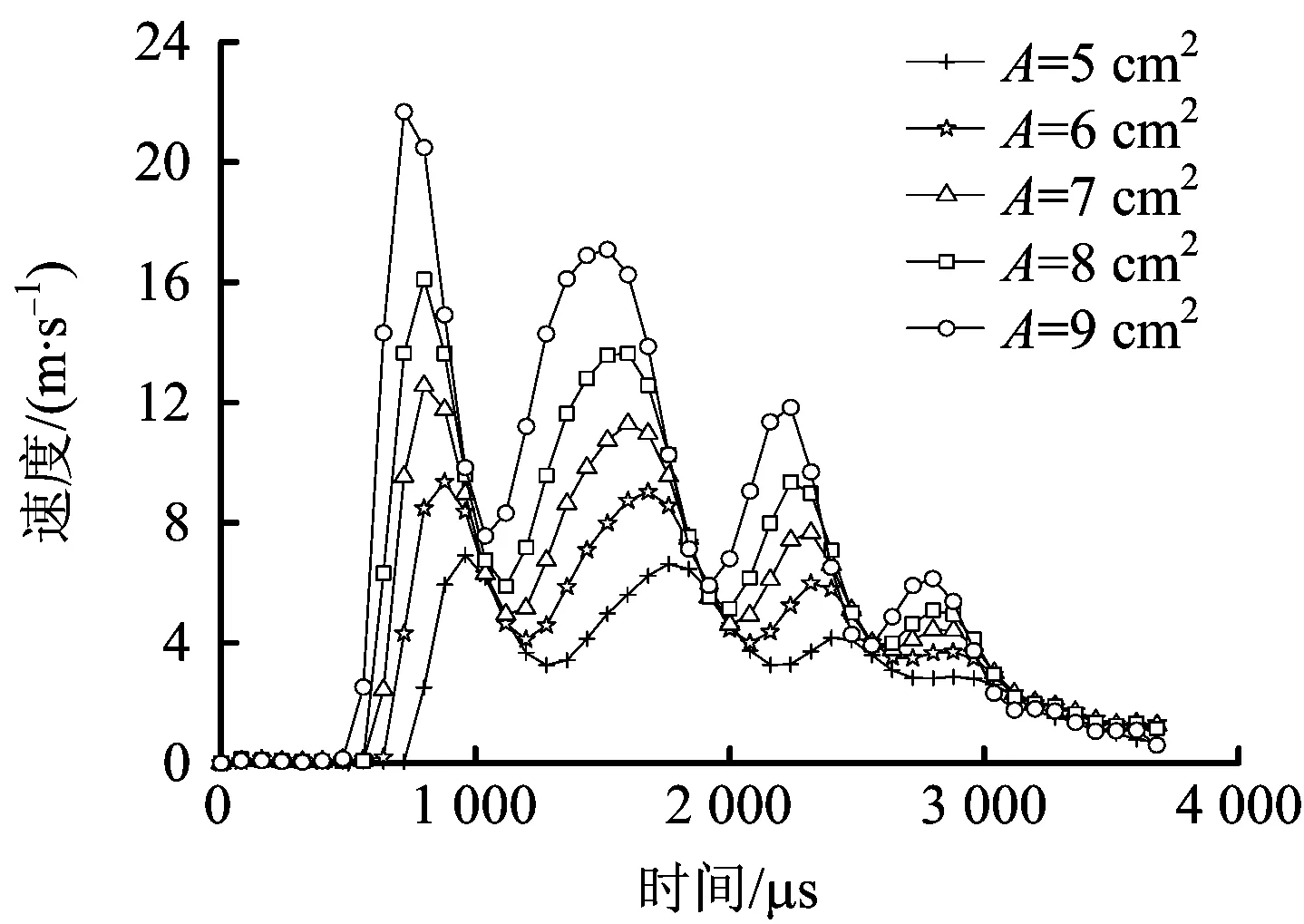
图8 速度时程Fig.8 Time history of velocity
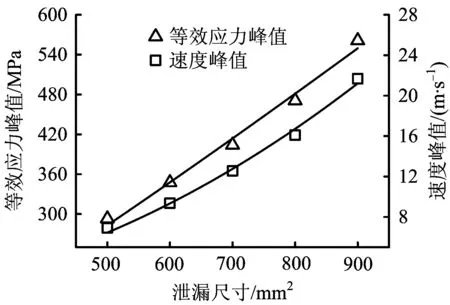
图9 管道的动力响应峰值Fig.9 The maximum dynamic response of pipeline
如图7和图8所示,在5种泄漏尺寸下,管道的等效应力时程和速度时程变化趋势一致。管道内压以初始应力的形式作用在管道上,在爆炸荷载的反方向作用下,管道的等效应力有减小的趋势。随着爆炸过程的进行,等效应力会增大直至峰值,然后在衬砌的反射和空气的耗散下,不断在初始应力附近波动。由图9可知,管道最大等效应力σ和速度峰值v与泄漏尺寸A成正相关,拟合出的关系式分别为:σ=46.017A1.129和v=0.248A2.025。孔口面积越大,等效应力和速度峰值越大。孔口面积由500 mm2增至900 mm2,对应的等效应力峰值从293 MPa增至561 MPa,速度峰值则从6.92m/s增至21.70 m/s。即泄漏尺寸增加80.0%,等效应力峰值增幅为91.5%,变化率为1.14;速度峰值增幅为213.6%,变化率为2.67。基于A组数据,当泄漏孔面积为805 mm2时,邻管达到屈服极限。
3.3 不同爆炸距离
选取表1中的B组数据,模拟在不同爆心距下管道的动力响应,见图10~图12。
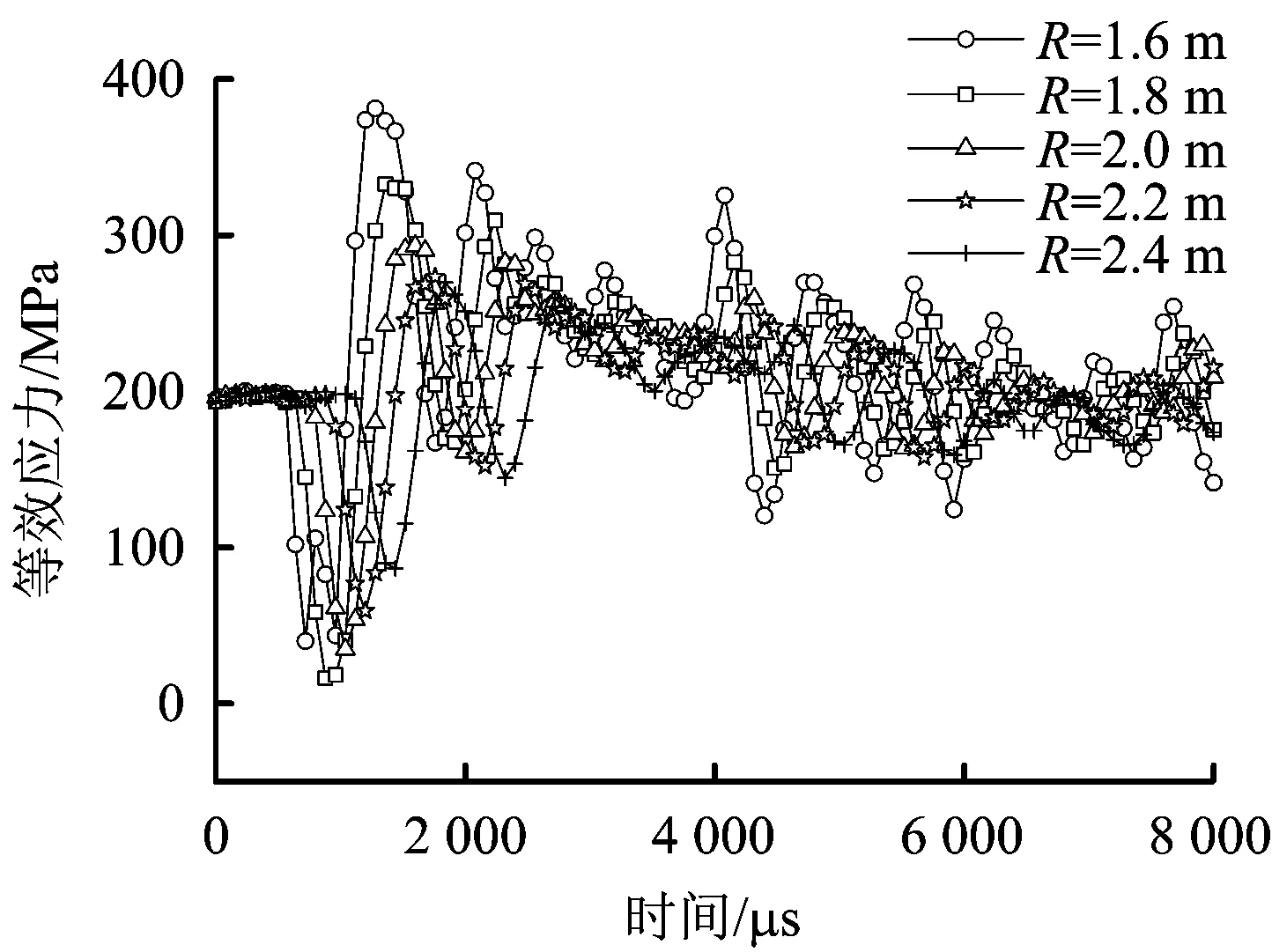
图10 等效应力时程Fig.10 Time history of effective stress
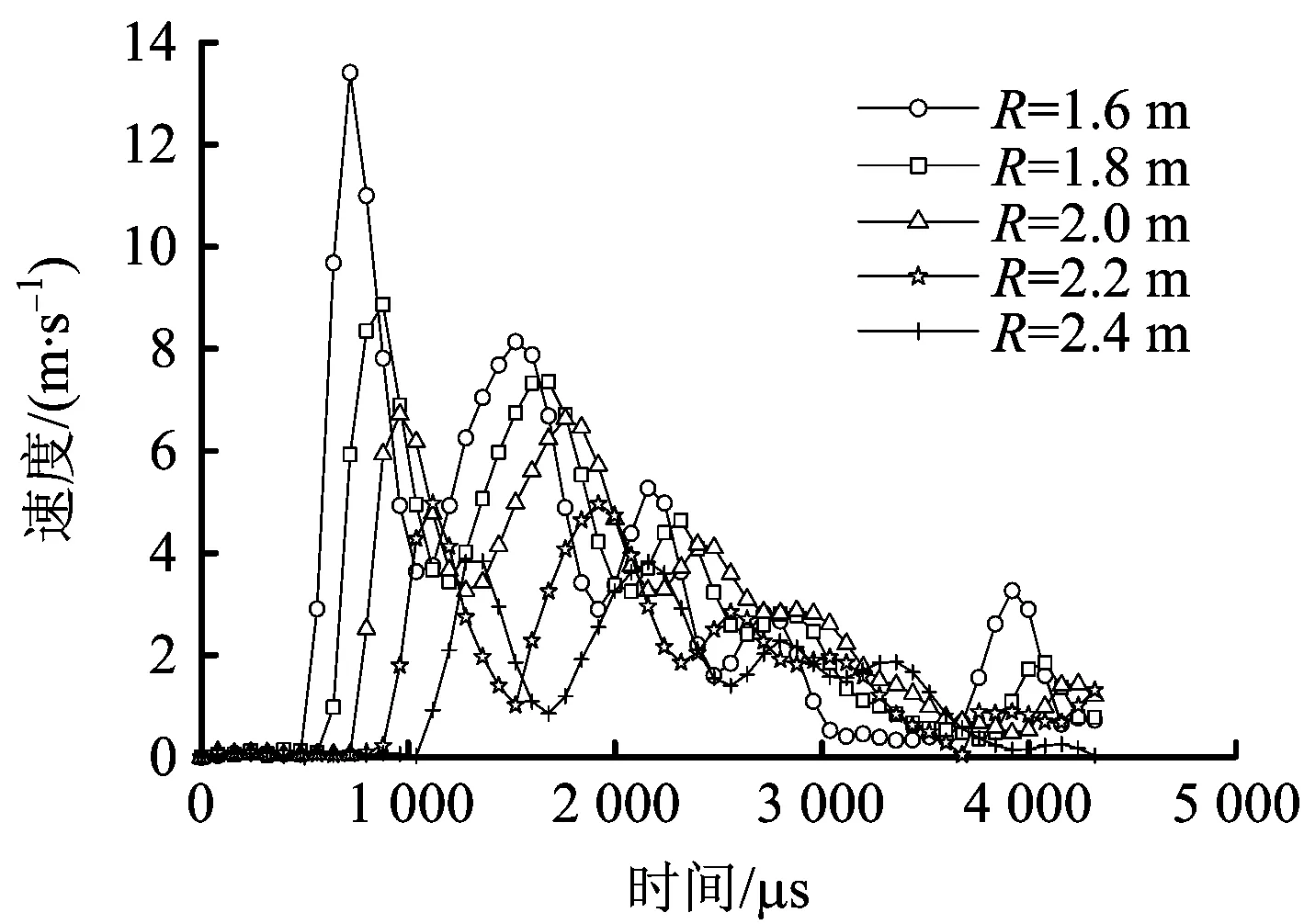
图11 速度时程Fig.11 Time history of velocity
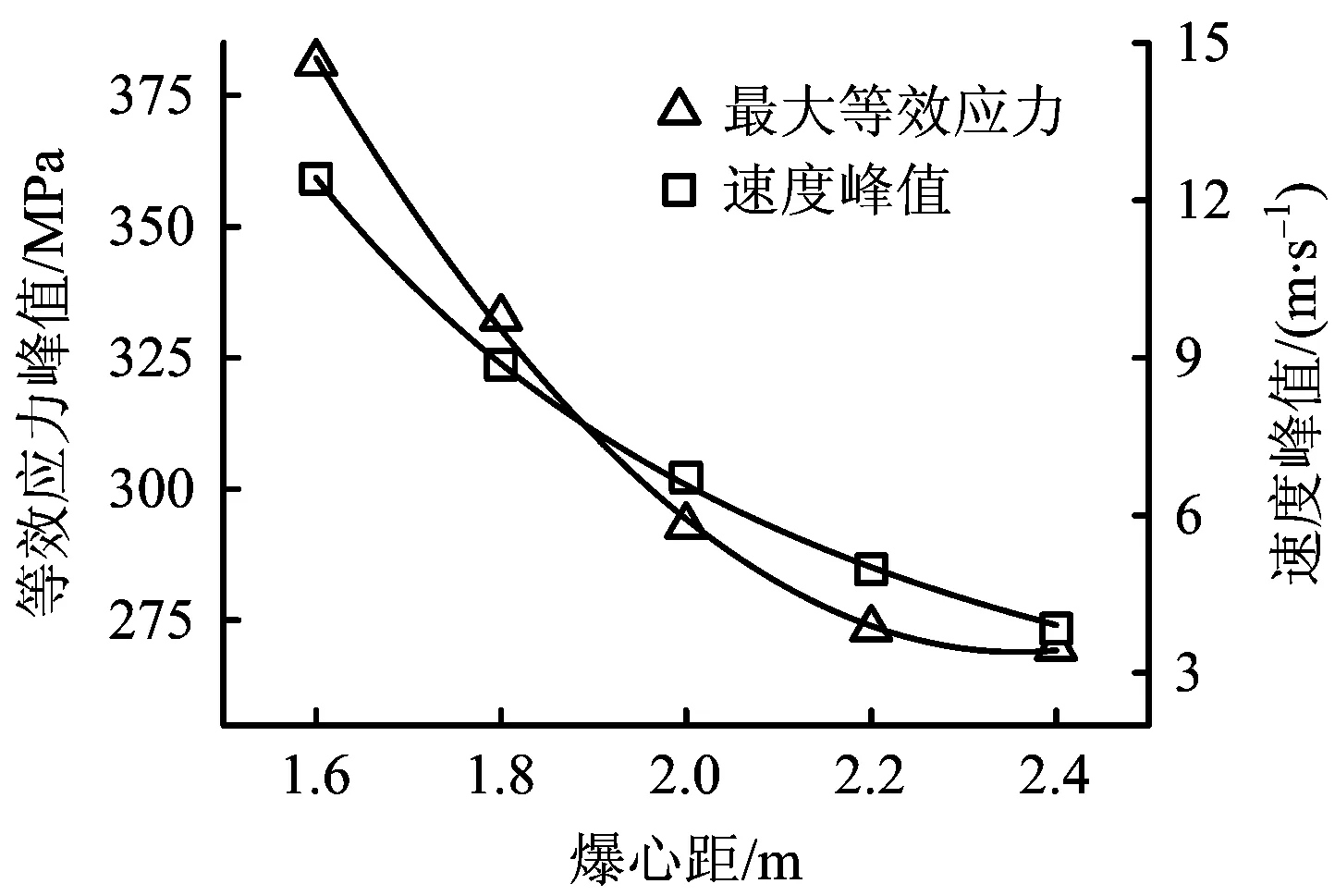
图12 管道的动力响应峰值Fig.12 The maximum dynamic response of pipeline
由图10和图11可知,爆心距由1.6 m等距增至2.4 m的过程中,等效应力峰值到达的时间依次滞后80.7,319.3,480.8和559.7 μs;速度峰值依次滞后159.6,240.4,400.0和640.4 μs。图12表明,爆心距越小,管道的动力响应越大。管道的最大等效应力σ和速度峰值v与爆心距R的关系式分别为:σ= 1 361.380-926.065R+196.262R2和v=47.469R-2.851。爆心距由1.6 m增至2.4 m,管道等效应力峰值从381.17 MPa减至269.79 MPa;速度峰值则从13.41 m/s减至3.84 m/s。即爆心距增加50%,管道的最大等效应力减幅为29.2%,变化率为0.58;速度峰值减幅为71.4%,变化率为1.43。基于B组数据,当爆心距减至1.31 m时,邻管开始屈服。
3.4 不同风速
对于管隧结构的爆炸数值模拟,风速直接影响蒸气云泄漏扩散的程度。选取表1中的C组数据,模拟出管道的动力响应,见图13~图15。
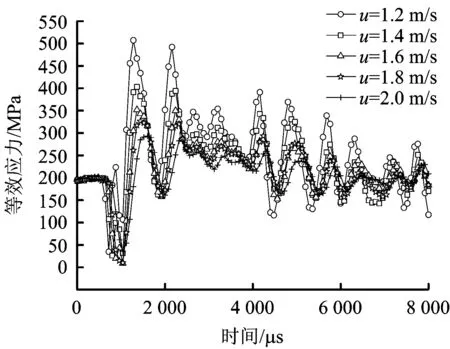
图13 等效应力时程Fig.13 Time history of effective stress
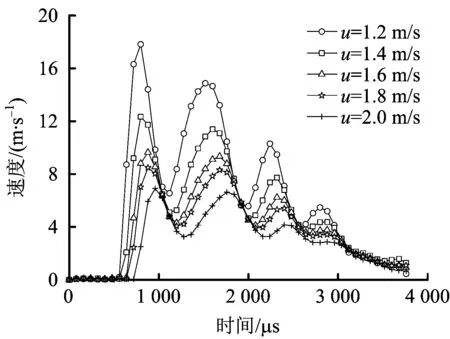
图14 速度时程Fig.14 Time history of velocity

图15 管道的动力响应峰值Fig.15 The maximum dynamic response ofpipeline
图13和图14表明,随着风速的增大,管道的最大等效应力和速度峰值减小。因为风速越大,蒸气云扩散越快,导致爆炸气体浓度越小,等效的TNT当量越小,即管道的动力响应越小。由图15可知,管道的最大等效应力(σ)和速度峰值(v)与风速(u)的关系分别为:σ=1 521.984-1 209.331u+298.985u2和v=24.649u-1.904。风速从1.2 m/s增至2 m/s,管道的最大等效应力从507 MPa减至293 MPa;速度峰值从17.82 m/s减至6.92 m/s。即风速增加66.7%,管道最大等效应力减幅42.2%,变化率为0.63;速度峰值减幅61.2%,变化率为0.92。基于C组数据,当风速小于等于1.23 m/s时,邻管会发生塑性变形。
4 结论
1)管道对爆炸作用的响应是内压和爆炸荷载共同作用的结果。隧道内爆炸冲击波经过衬砌的不断反射和叠加,管道的等效应力和速度会出现多个峰值,爆炸冲击波只产生一个显著的波峰。
2)通过隧道内并行管道的爆炸数值模拟,得出了管道的动力响应与泄漏尺寸、爆心距和风速的关系。其中,管道的最大等效应力和速度峰值对泄漏尺寸的变化最敏感,变化率分别为1.14和2.67。在不同的泄漏尺寸和风速下,管道的动力响应时程变化趋势一致;而在不同的爆心距下,管道的动力响应峰值有明显的滞后现象。在一定的条件下,管道泄漏尺寸越小、管间距越大以及风速越大,爆炸导致邻管失效的可能性越小。
3)本文提出的计算方法较好地描述了隧道内管道发生爆炸后对邻管的动力响应,数值模拟结果与经验公式计算结果比较吻合,为隧道并行输气管道在爆炸荷载作用下的后果严重度评估提供了一种新的计算方法。
[1]向波,陈静,杨帆,等. 中卫-贵阳输气管道的创新设计研讨[J]. 天然气与石油, 2010,28(5):1-5.
XIANG Bo,CHEN Jing,YANG Fan,et al. Research on innovative design of gas pipeline along zhongwei and Guiyang[J]. Natural Gas and Oil,2010,28(5):1-5.
[2]秦玉新,荣军,王奉生,等. 陕京三线输气管道与石楼-顺义成品油管道共用隧道设计[J]. 石油化工设备,2015, 44(6):36-39.
QIN Yuxin,RONG Jun,WANG Fengsheng,et al. Shared tunnel design of shanxi-beijing gas pipelineIII and shilou-shunyi pipeline[J]. Petro-Chemical Equipment,2015, 44(6):36-39.
[3]周子栋,林罡,徐娜,等. 中缅油气管道(国内段)工程建设难点及对策[J]. 石油工程建设,2014,40(4):52-54.
ZHOU Zidong,LIN Gang,XU Na,et al. Construction difficulties and countermeasures of domestic pipeline section of Myanmar-China oil and gas pipeline[J]. Petroleum Engineering Construction,2014,40(4):52-54.
[4]高云宇,魏仁军,易志军,等. 果子沟隧道内同时敷设两根管道施工技术创新[J]. 石油工程建设,2010, 36(S1):226-229.
GAO Yunyu,Wei Renjun,YI Zhijun,et al. The innovation of construction technology of two pipelines laying simultaneously in the tunnel[J]. Petroleum Engineering Construction,2010, 36(S1):226-229.
[5]MOKHTARI M, NIA A A. A parametric study on the mechanical performance of buried X65 steel pipelines under subsurface detonation[J]. Archives of Civil and Mechanical Engineering, 2015, 15(3): 668-679.
[6]J.Malachowski,L. Mazurkiewicz,R.Gieleta. Analysis of structural element with and without protective cover under impulse load,in: Proc. 12th Pan-American Congress of Applied Mechanics,January 2-6,Port of Spain,Trinidad,2012.
[7]高进东,韦春艳,周轶. 爆炸载荷下埋地管线动力学分析数值模拟[J]. 科技导报,2013,31(26):30-34.
GAO Jindong,WEI Chunyan,ZHOU Yi. Dynamic analysis of buried pipelines under blast loads with numerical simulation method[J]. Science & Technology Review,2013,31(26):30-34.
[8]姚安林,赵师平,么惠全,等. 地下爆炸对埋地输气管道冲击响应的数值分析[J]. 西南石油大学学报(自然科学版),2009,31(4):168-172.
YAO Anlin,ZHAO Shiping,ME Huiquan,et al. Numerical analysis of impact response of underground explosion on buried gas transmission pipeline[J]. Journal of Southwest Petroleum University(Science & Technology Edition),2009,31(4):168-172.
[9]GIANNAROS E, KOTZAKOLIOS T, KOSTOPOULOS V. Blast response of composite pipeline structure using finite element techniques[J]. Journal of Composite Materials, 2016, 50(25): 3459-3476.
[10]WON J H, KIM M K, KIM G, et al. Blast-induced dynamic response on the interface of a multilayered pipeline[J]. Structure and Infrastructure Engineering, 2014, 10(1): 80-92.
[11]刘富君,凌张伟,孔帅,等. 天然气管道泄漏扩散实时计算与燃爆危害预测研究[J]. 压力容器,2010,27(10):21-29.
LIU Fujun,LING Zhangwei,KONG Shuai,et al. Research on the realtime calculation of gas leakage and diffusion and hazards prediction of fire and explosion for nature gas pipeline[J]. Pressure Vessel,2010,27(10):21-29.
[12]魏韡. 爆炸冲击荷载下油气管道的动态响应分析与安全评价[D]. 西南石油大学,2014.
WEI Wei. Dynamic response analysis and safety evaluation of oil and gas pipeline under blast loading[D]. Southwest Petroleum University,2014.
[13]金军. 蒸气云爆炸事故的风险评估方法[J]. 消防技术与产品信息,2014(12):25-27.
JIN Jun. Risk assessment method of vapor cloud explosion[J]. Fire Technique and Products Information, 2014(12):25-27.
[14]纪冲,龙源,唐献述,等. 爆炸载荷下X70钢管道的局部破坏效应[J]. 高压物理学报,2013,27(4):567-574.
JI Chong,LONG yuan,TANG Xianshu,et al. Local damage effect of X70 steel pipeline under blast loading[J]. Chinese Journal of High Pressure Physics,2013,27(4):567-574.
[15]胡春红,周晶.炸药量和场地条件对水下爆炸地震波影响的数值模拟[J].爆破,2007,24(3):11-15, 32.
HU Chunhong,ZHOU Jing. Numerical simulation of the influence of explosive quantity and site conditions on underwater explosion seismic wave[J]. Chinese Journal of explosion, 2007, 24(3): 11-15,32.

