集对分析理论在爆破工程安全预评价中的应用*

陈雪锋，陈文涛

(1.北京科技大学 土木与资源工程学院，北京 100083；2.中国职业安全健康协会，北京 100013)

0　引言

随着国家建设发展，爆破技术在基础建设、矿山开采等领域得到了广泛的应用。爆破能够加快工程建设速度，节省建造成本，给工程建设带来极大的便利。然而，爆破工程作业过程中一旦发生生产事故，将会造成严重的经济损失和恶劣的社会影响。因此，为了保障人的生命和财产安全，确保爆破工程的顺利实施，对爆破工程进行科学合理的安全预评价，具有重要的现实意义[1]。

爆破工程安全受设计方案、施工过程、爆区环境等多种因素影响，是一种多因子的综合评价。目前，爆破工程安全预评价方法主要采取预先危险性分析法、模糊综合评价法、灰色关联分析方法等[2-4]，这些方法虽然考虑了爆破安全影响因素的模糊性，但并没有考虑到安全影响因素的不确定性问题，因而存在一定的局限性。集对分析理论正是一种用于处理模糊和信息不确定性系统的理论和方法，其核心思想是把不确定性与确定性视为一个既确定又不确定的同异反系统进行分析和数学处理[5]，且在水质评价、自然灾害风险度评价、工程造价风险评价等方面得到了成功应用[6-8]，很好地解决了影响因素的不确定性问题。鉴于此，以下将集对分析理论应用于爆破工程安全预评价，以期为同类施工提供借鉴和参考。

1　爆破工程安全预评价指标体系

1.1　爆破工程安全预评价指标体系构建

影响爆破工程安全的因素很多，有爆破设计方案、施工过程中的影响因素，又与爆区环境条件密切相关，而且通过大量的调查分析表明，安全管理也是分析事故致因不可或缺的因素之一。在以往研究成果的基础上，遵循全面性、简洁性、可操作性原则[9]，并结合有关法律法规及规程，构建爆破工程安全预评价指标体系，如图1所示。

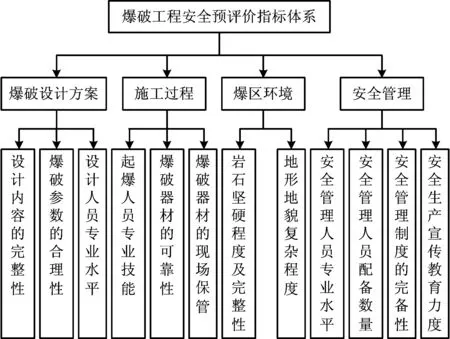
图1　爆破工程安全预评价指标体系Fig.1　Indexes system of blasting engineering safety pre-evaluation

1.2　爆破工程安全预评价指标权重确定

合理地确定各指标权重是实现科学合理评价的关键问题之一。常见的指标权重计算方法分为主观赋权法和客观赋权法。主观赋权法具有利用专家知识的优点，但存在较大的主观性。因此，以下采取客观赋权法中的熵值法，即文献[10]中的方法来计算权重，以降低这种主观性，计算结果见表1。

2　基于集对分析理论的爆破工程安全预评价

2.1　集对分析理论

集对分析是我国学者赵克勤于1989年提出的一种处理不确定性问题的系统分析方法，其基本思想是从同一、差异和对立等3个方面系统描述2个被比较对象的关系[11]。集对分析理论有3个基本概念：集对、联系度和集对势。所谓集对，是指具有一定联系的两个集合组成的一个对子。如给定2个集合A和B，则用H=(A，B)表示2个集合组成的对子。在具体背景下，联系度用来对集对H=(A，B)的特性展开数学分析，其表达方式如下:

μ=a+bi+cj(1)

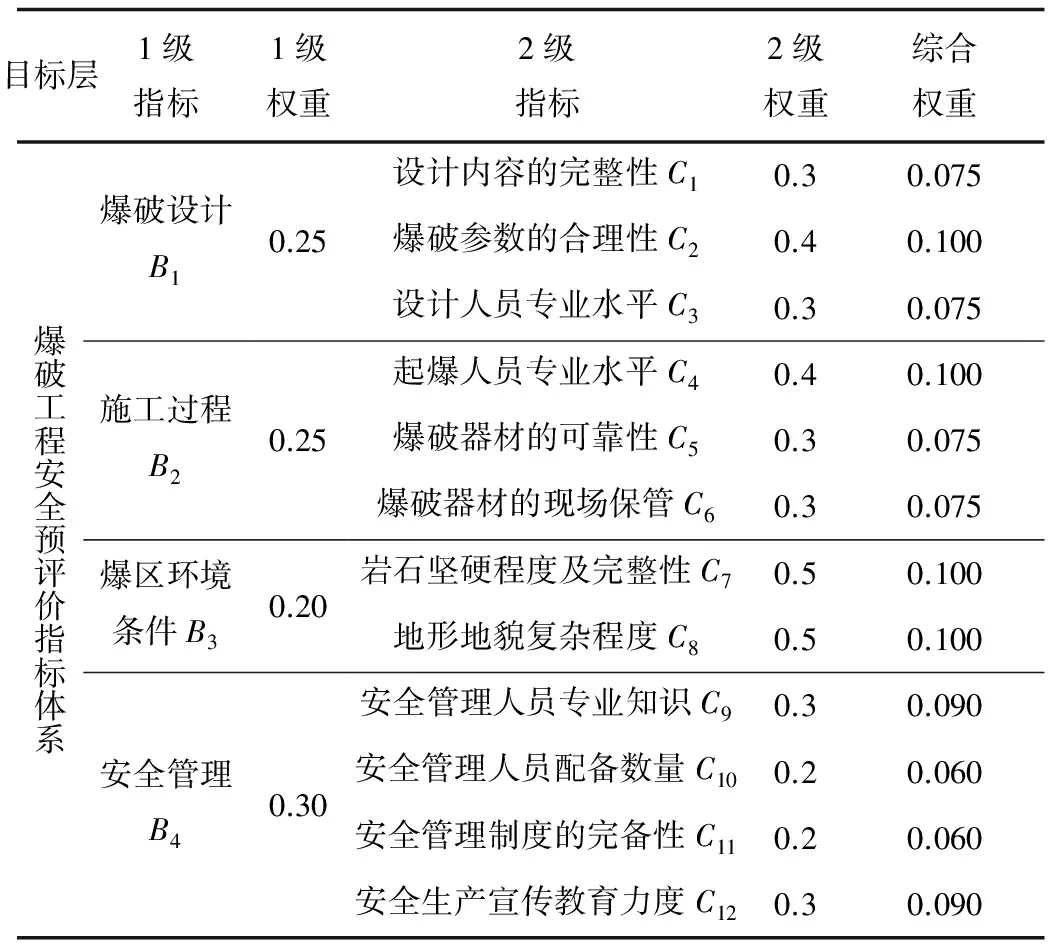
表1　爆破工程安全预评价指标权重

式中：μ为联系度；a，b，c分别为集合A和集合B的同一度、差异度和对立度，且满足归一化条件，即：a+b+c=1；i为差异度系数，取值范围为[-1，1]；j为对立度系数，取值为-1。

式(1)称为三元联系数表达式。在实际应用中，如果将bi分解为n个级别，则将三元联系数引申为多元联系数，即：μ=a+bi1+b2+…+bn+cj，称之为n+2元联系数[12]。

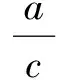
由式(1)可知，联系度是从同一、差异和对立等3个方面全面描述2个事物的确定与不确定性信息，其中，bi反映集合A和集合B的差异性，bi随着i的变化而变化，属于不确定性信息；a和cj分别体现集合A和B的同一性和对立性，属于确定性信息，故联系度充分考虑了事物的确定性与不确定性，从而能够更加准确地处理事物的模糊性。

2.2　基于集对分析理论的爆破工程安全预评价模型

在基于集对分析理论的爆破工程安全预评价模型中，将安全评价结果和安全评价标准一起构成一个集对。

2.2.1安全评价等级划分

在安全评价过程中，需要制定合理的安全评价等级。在实际应用中，通常将安全评价等级划分为奇数个等级[13]，本文将爆破工程安全分为5个等级，具体见表2。

表2　安全等级表

2.2.2五元联系数确定

根据安全评价等级划分，采取五元联系度进行集对分析，表达式为：

u=o+pi1+qi2+ri3+sj

(2)

式中：o+p+q+r+s=1；u表示评价结果与评价标准的联系度；o，p，q，r和s分别表示“很安全”、“较安全”、“安全”、“不安全”和“很不安全”的程度。

假设指标Ci(i=1，2，…，n)综合权重为Wi(i=1，2，…，n)，则式(2)可表示为：

(3)

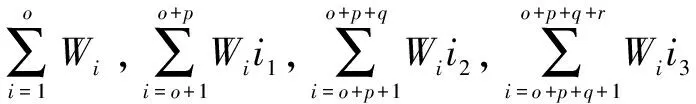
2.2.3五元联系数模型

邀请n位专家对各指标进行评价，根据专家的业务水平和知识，设专家权重W为[W1，W2，…，Wn]，令μ′(M)为n位专家对指标评价结果的五元联系数计算模型，则：

(4)

式中：R为同异反评价矩阵；E为联系分量矩阵；M代表模型“Model”。

2.2.4安全评价结果的判别

由于每种数学方法都存在局限性，为了防止评价结果失真，应对评价结果进行辨别。根据文献[14]，假设o=max(o，p1，p2，p3，q)，则o>0.5为集对分析在判别系统归属级别的适用条件；同样，p1，p2，p3和q为最大值时，可以与o直接替换。如果不满足此适用条件，则利用系统各级别变量的全部信息来求出系统级别特征值，来判断系统的安全等级，系统级别变量的归属程度见表3。

表3　系统级别变量的归属程度

将各级别归属程度作为权重，其对应的级别特征值之积的总和作为系统的级别特征值，计算公式为：

(5)

式中：usum为系统级别特征值。

2.2.5集对势分析

表4　集对势的等级划分

3　应用实例

将上述建立的模型应用于江油市某烟囱拆除爆破工程进行安全预评价。

3.1　问卷调查

根据现场的实际情况，邀请5位专家进行问卷调查，得到原始数据见表5。

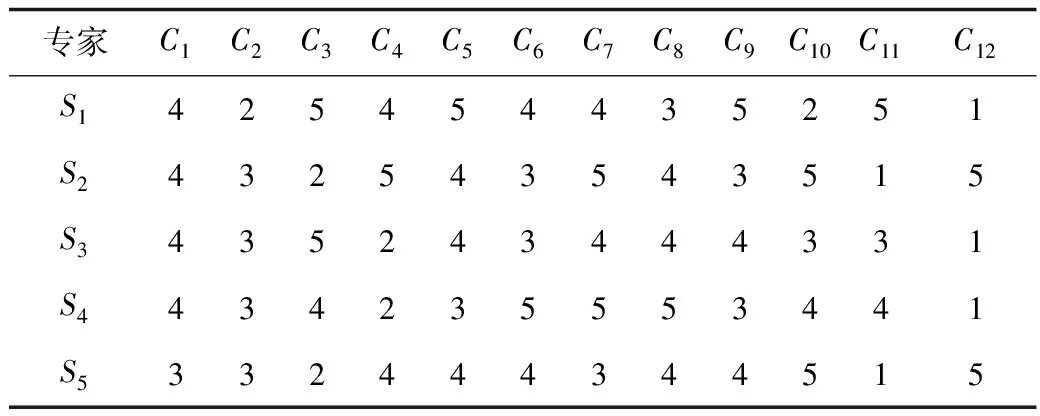
表5　爆破施工安全预评价指标调查表

3.2　安全评价联系数计算

根据5位专家评价结果和各项评价指标的权重，根据式(3)计算，得出每个专家所对应的安全评价联系数，结果见表6。

表6　爆破工程安全评价联系数

3.3　安全评价结果计算

依据专家的业务水平和知识，5位专家的权重W=(0.25，0.15，0.20，0.15，0.25)，结合式(4)，可以得出该次拆除爆破工程的综合安全评价联系式为：

0.221 25+0.363 500i1+0.193 25i2+0.144 00i3+0.078 00j

3.4　安全评价结果分析

由于o=max(o，p1，p2，p3，q)=0.363 5<0.5，故采取式(5)求出系统特征值，即：

usum=0.221 25×5+0.363 5×4+0.193 25×3+0.144×2+0.078×1=3.506

根据说明本次爆破工程处于“安全”与“较安全”之间。

3.5　集对分析势分析

4　结论

1)从爆破设计、施工过程、爆区环境和安全管理等4个因素中选取设计内容的完整性、爆破参数的合理性、设计人员专业知识等12个指标构建爆破工程安全预评价指标体系；采取熵值法计算指标权重，能够减少指标权重赋值的主观性。

2)针对诸多指标具有模糊性，难以确定的特点，建立基于集对分析理论的爆破工程预评价模型，且将该模型应用于工程实例，实例应用表明，该模型能够应用于爆破工程的安全预评价，可以为爆破工程顺利开展提供决策依据。

[1]张云鹏，于亚伦．爆破工程安全评价初探[J]．工程爆破，2004，10(4)：81-84，77．

ZHANG Yunpeng，YU Yalun．A preliminary study on appraisement of blasting engineering safety[J]．Engineer Blasting，2004，10(4)：81-84，77．

[2]张黎明，池恩安，赵明生，等．模糊综合评价法在岩土爆破安全评价中的应用[J]．工程爆破，2015，21(2)：13-17.

ZHANG Liming，CHI En’an，ZHAO Mingsheng，et al．Application of fuzzy comprehensive evaluation in rock-soil blasting safety assessment[J]．Engineer Blasting，2015，21(2)：13-17.

[3]李科斌，周俊珍，马海鹏，等．PHA法在高耸烟囱拆除爆破安全评价中的应用[J]．采矿技术，2013，13(5)：134-137.

LI Kebin，ZHOU junzheng，MA Haipeng，et al．PHA method in the application of the tall chimney demolition blasting safety assessment [J]．Ming technology，2015，21(2)：13-17.

[4]黄永辉.灰色理论在非煤矿山爆破评估及预测中的应用研究[D]．昆明：昆明理工大学，2009.

[5]李德顺，许开立，张喜嘉，等．集对分析集对势的研究及其应用[J]．工业安全与环保，2009，35(9)：8-9，17.

LI Deshun，XU Kaili，ZHANG Xijia，et al．Research and application of set pair situation in the set pair analysis[J]．Industrial Safety and Environment Protection，2009，35(9)：8-9，17．

[6]卢敏，张展羽，石月珍．集对分析法在水安全评价中的应用研究[J]．河海大学学报(自然科学版)，2006，34(5):505-508．

LU Min，ZHANG Zhanyu,SHI Yuezhen．Application of set pair analysis to evaluation of water safety[J]．Journal of Hohai University(Natural Science)，2006，34(5):505-508．

[7]王文圣，金菊良，李跃清．基于集对分析的自然灾害风险度综合评价研究[J]．四川大学学报(工程科学版)，2009，41(6)：6-12.

WANG Wensheng，JIN Juliang，LI Yueqing．Risk degree assessment of natural disaster based on set pair analysis method[J]．Journal of Sichuan University(Engineering Science Edition)，2009，41(6)：6-12．

[8]文洁．集对分析法在工程造价风险评估中的应用研究[D]．长沙：湖南大学，2013．

[9]罗德江，吴尚昆，郭科．基于组合权-灰色关联分析法的矿产资源开发利用综合评价[J]．金属矿山，2015(2)：20-25．

LUO Dejiang，WU Shangkun,，GUO ke．The comprehensive evaluation of evaluation and utilization efficiency of mineral resources based on combination weight and gray relation analysis method[J]．Metal Mine, 2015(2):20-25.

[10]陈雪锋，蒲传金，肖定军，等．基于熵理论的邻近天然气管道爆破施工风险评价[J]．现代矿业，2016(2)：147-149, 152．

CHEN Xuefeng，PU Chuanjin，XIAO Dingjun，et al．Study on risk evaluation mode of blasting construction near natural gas pipeline[J]．Modern Mining，2016(2)：147-149, 152．

[11]曹文贵，翟友成，王江营，等．山岭隧道塌方风险的集对分析方法[J]．中国公路学报，2012，25(2)：90-99．

CAO Wengui，ZHAI Youcheng，WANG Jiangying，et al．Method of set pair analysis for collapse risk during construction of mountain tunnel[J]．China Journal of Highway and Transport，2012，25(2)：90-99．

[12]刘保相．粗糙集对分析理论与决策模型[M]．北京：科学出版社，2010．

[13]魏勇，许开立．集对分析法在尾矿坝稳定性安全评价中的应用[J]．中国安全生产科学技术，2012，8(9)：101-105．

WEI Yong，XU Kaili．Application of set pair analysis on safety evaluation of tailing dam stability[J]．Journal of Safety Science and Technology，2012，8(9)：101-105.

[14]刘祖德，万福威．多元联系数集对分析在安全绩效评价中的应用[J]．中国安全科学学报，2014，24(5)：138-143．

LIU Zude,，WAN Fuwei．Research on application of multiple connection number set pair analysis in safety performance evaluation[J]．China Safety Science Journal，2014，24(5)：138-143．

[15]谭翀，陆愈实，车恒．集对分析法在露天采石场安全评价及预测中的应用[J]．安全与环境学报，2016，16(3)：25-29．

TAN Chong, LU Yushi，CHE Heng．On the application of the set pair analysis method to the safety evaluation and prediction of the open rock quarry[J]．Journal of Safety and Environment，2016，(3)：25-29.