平面界面折射成像位置的研究

郎 军 董洪琼

(重庆市第十一中学校，重庆 400061)

平面界面折射成像位置的研究

郎 军 董洪琼

(重庆市第十一中学校，重庆 400061)

应用几何画板软件根据折射定律对平面界面折射成像位置进行研究,得到了精确的定量结果,用实验对研究结果进行检验,发现理论结果与实验观测严重不符.通过分析,发现了传统分析中确定像点方法有重大疏漏.通过研究微小立体角光束的反向交汇点来确定平面界面折射成像位置,得到的理论结果与实验观测一致.

平面界面;折射;成像位置;立体角光束

1 问题的提出

图1

在岸上观察水中物体,像的位置在哪里呢?通常研究方法是在图1所示的平面内取两条夹角很小的入射光线,应用折射定律定量计算两折射光线反向延长线的会聚点,这个点就是像的位置.研究得到的结论是:相对于物点而言,像点在竖直方向要上移,在水平方向要靠近观察者，这是大家熟知的结论.然而在实际观察中发现,像点在水平方向移动不明显.对此中学阶段目前有两种观点.

观点1:通常情况下像点的水平偏移量很小,以致于人眼感觉不到.

观点2:由于观察方向的原因,像点的水平偏移无论多大都看不出来.

观点2很具有欺骗性,当用单眼观察物体时,人眼的确对距离的变化不是很敏感,但人是双眼观察,可以通过观察目标对两眼的夹角大小来判断物体的远近,只有当物体很远时,物体对两眼夹角小于人眼分辨角后,人对距离的变化才不敏感.

在图1中,设物点A经水面折射后理论上成像于A′点,相对于物点,像点的竖直位移为Δy, 水平位移为Δx.注意这种情况下,人眼观察的视线也并不是沿水平方向,视线与水平位移Δx和竖直位移Δy都不平行,凭什么人眼只能感受到Δy却感受不到Δx呢?

折射像和反射像尽管都是虚像,但人眼对它们的视觉感受与看实物是一样的.像不是影,观察虚像的位置不是人眼“发出”光将虚像投影.所以图1中人眼看到的像点的位置就在它实际的位置A′,只要水平偏移足够大,人眼是能感受到的.

为了进一步弄清真相,我们作了比较深入的研究,获得了令人意外的发现.

2 深度研究

研究的主要思路是先得出在不同视角下折射像点偏移量的理论数据,然后用实验测出在同等条件下折射像点偏移量的实验数据,最后对理论结果与实验结果进行比较分析.

2.1 用几何画板定量探究物点经平行玻璃砖折射成的像点偏移量的理论数据

用几何画板软件进行研究的界面设置如图2所示,软件严格按折射定律作图,物点S发出的光经两次折射后成像于S′,出射点C与S′的反向延长线与SO交于S″．重新设置参数Δi=0.001°及物点S距下界面的距离为0.01cm,界面变成图3所示．

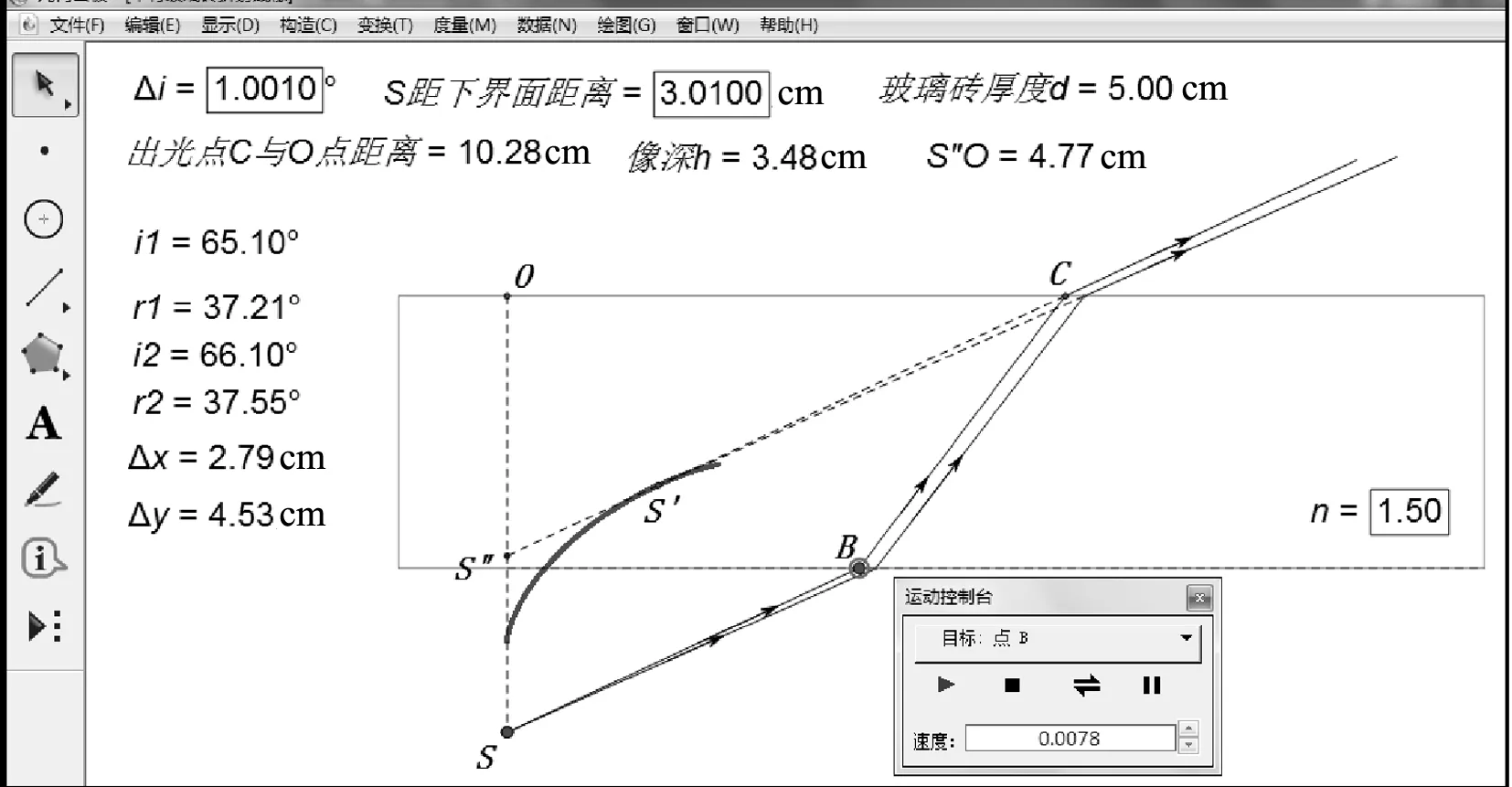
图2

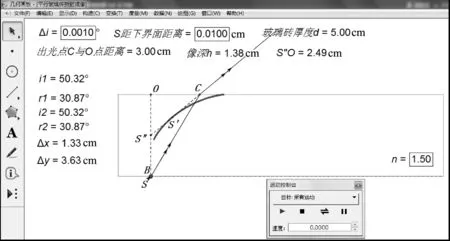
图3

选取S′后设置“追踪点”,调出“运动控制台”窗口,选取动点B点,调节播放速度至最慢,按播放按钮,屏上显示出沿不同方向观察对应像点S′的变动轨迹,随时暂停可记录不同视角下的偏移数据.得到的理论数据如表1所示.

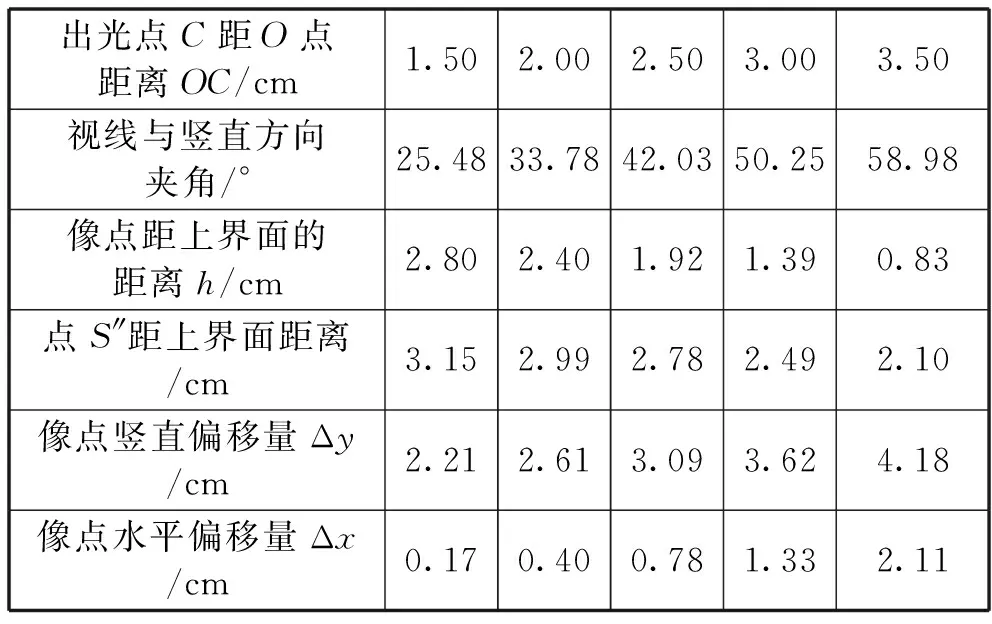
表1 物点经平行玻璃砖折射成像偏移量的理论数据(d=5.0cm,n=1.50)

数据表明,当视角(视线与竖直方向夹角,下同)较小时,像的水平偏移量确实很小,但当视角较大时,像的水平偏移量就不小了,视角约为60°时,水平偏移量将是竖直偏移量的一半,这么大的偏移无论如何应该能用实验观察出来.

2.2 测量折射像点偏移量的实验数据

实验装置原理图和实物图分别如图4和图5所示.物点为在白纸上画的5个点,中间点为研究对象,边缘4个点为参照点.实验前调节玻璃砖的位置,让过中点S点的竖直面与固定标尺的零刻度相交.打开手电筒(可用手机代替),顺着观察的方向补光,调节补光方向以便能同时看清物点的折射像和竖直活动标尺的反射像,调节竖直标尺的位置,让它的反射像的刻度线穿过折射像点S′.通过两个标尺的刻度可以确定像点S′的位置,保持视线不变,调节遮光片的位置至恰能看到像点的一半,通过遮光片所对的刻度可以确定光线出射点的位置坐标,结合像点S′的坐标进一步可以算出视角等.

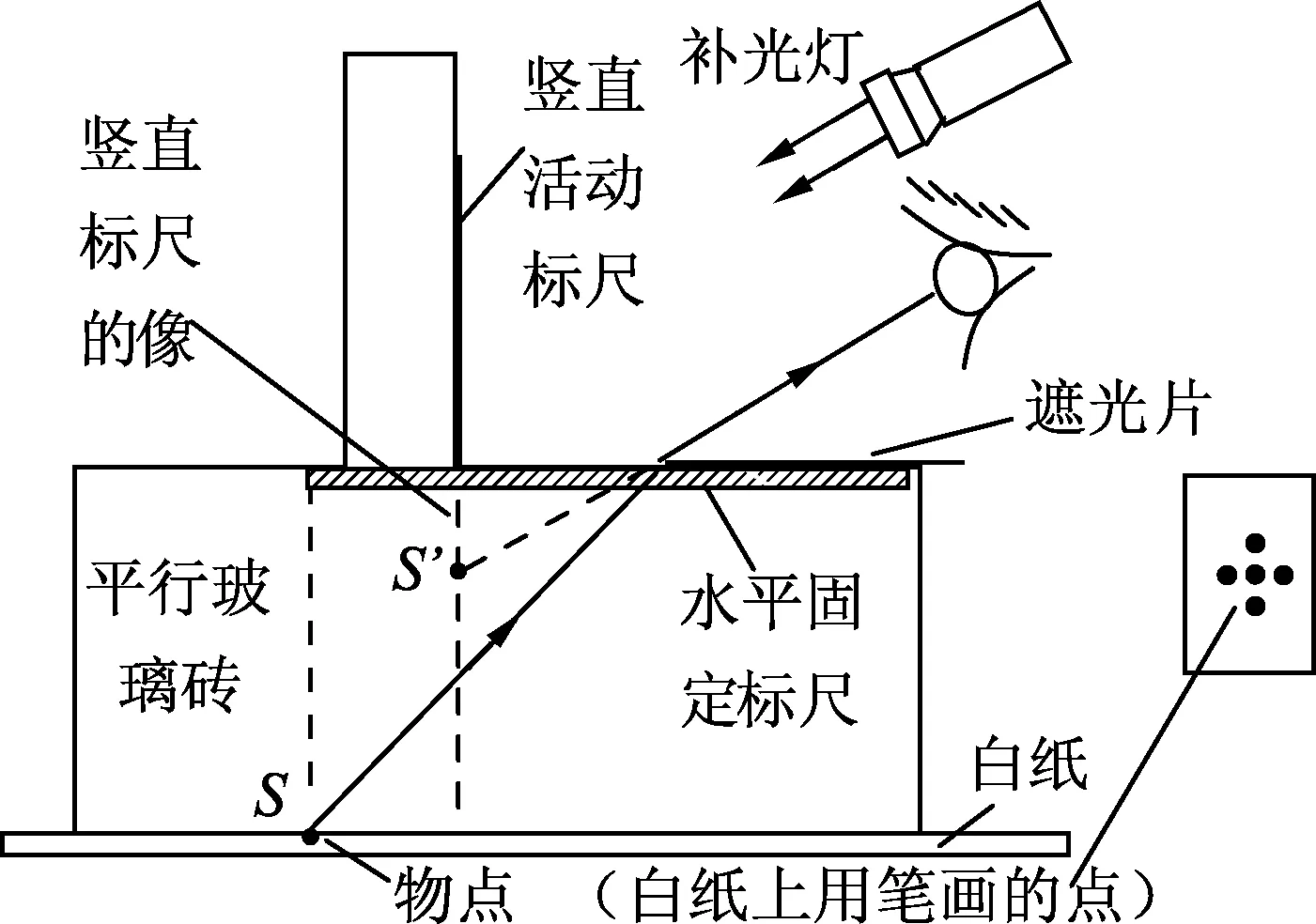
图4

图5

连续缓慢地改变观察方向,并随之调整补光方向,观察折射像点的位置变化情况并记录有关数据.

本实验所用玻璃砖的厚度为d=5.0cm,折射率约为1.50,观测的数据如表2所示.

表2 观察玻璃中物点的折射像偏移量的实验数据(d=5.0cm,n=1.50)

观察发现,活动标尺不需要作任何移动(稍微移动一下活动标尺,像点S′就会偏离标尺反射像的竖直线),它一直对准固定标尺的零刻度.随着视角的增大,折射像点沿标尺反射像的竖直线上升而逐渐变得模糊,但始终未偏离这条竖直线.

实验表明,折射像点在水平方向零偏移,在竖直方向的偏移也与理论结果有较大的差异.很显然,这么大的差异不可能是读数误差和玻璃折射率不准造成的.

对比表1和表2的数据不难发现,实验观察到的像点并不是在图3中S′,而是在S″的位置．

图6～8是用几何画板研究的从岸上同一观察点看水中竖直杆OA的折射像的理论结果.理论结果表明,直杆的折射像要弯曲,当观察方向与竖直方向达到70°左右时,很大一部分直杆的折射像将几乎横卧在水平面上.

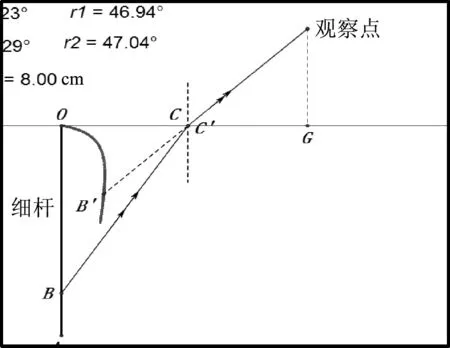
图6

图7

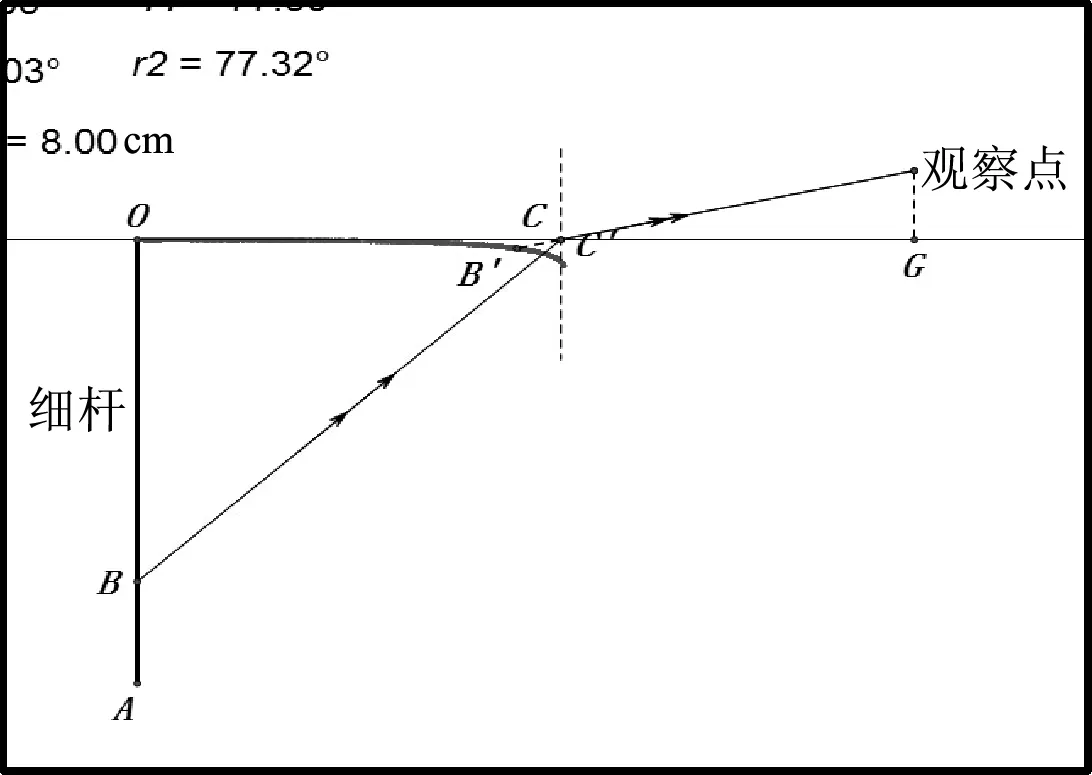
图8

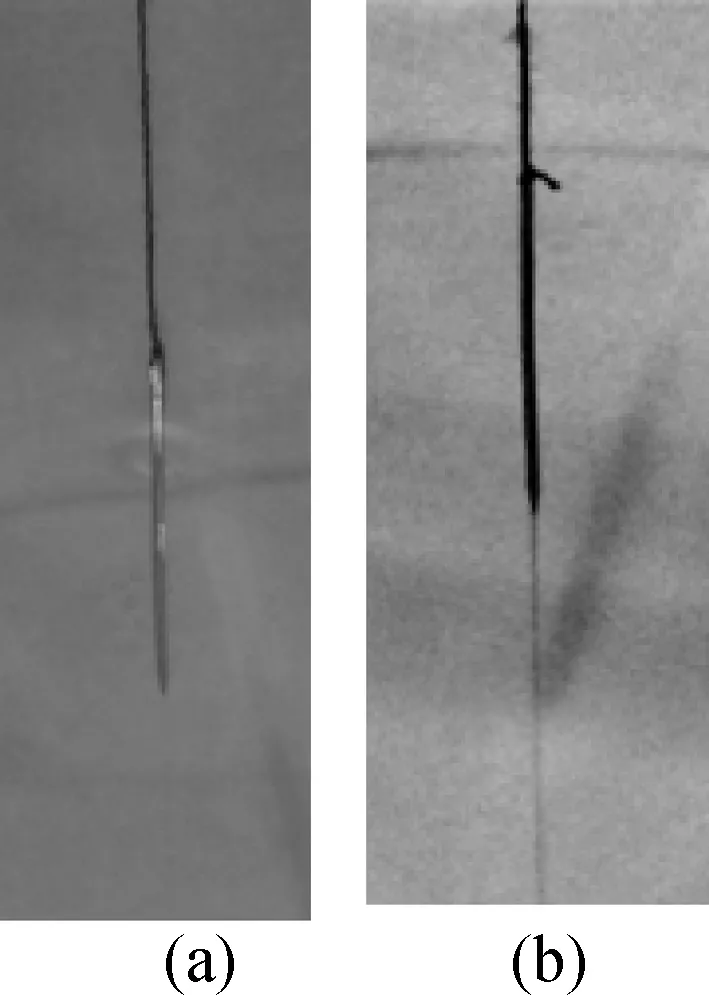
图9

我们用图9所示的实验进行检验.在实验时同样要注意沿观察的方向适当补光,以便能看清钢针的折射像和竖直悬线的反射像.(a)图中钢针有大半竖直插入水中,倾斜观察钢针与水面的交接处,看不到任何偏折.改变观察方向,水中钢针像的长度不断变化,但水面上下两部分钢针始终保持在同一条竖直线上.图(b)中钢针全部浸入水中,调节补光方向让细线的反射像清晰可见,随着视线与竖直方向夹角的变大,可以看到整个钢针不变形,只是长度逐渐变短,但始终保持竖直,针尖始终沿细线的反射像向上移动,始终看不到钢针的折射像偏离竖直方向的情况.

需要说明的是相机拍的照片远没有人眼看到的情况真切,希望读者不要仅从照片记录的结果来分析可能存在的观察错觉．

2.3 传统方法的错因分析

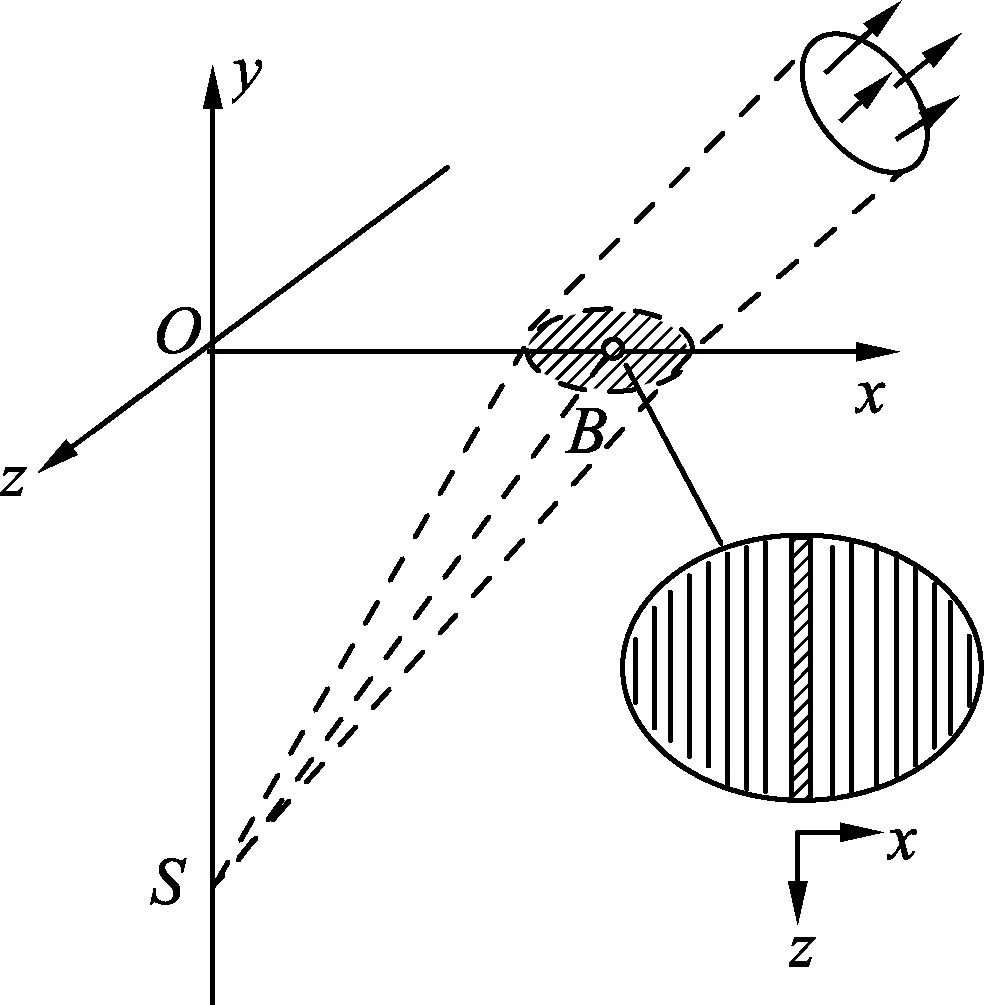
图10

物点发出的单心光束经平面界面反射后仍是单心光束,所以物点的反射像是严格的点像,所有反射光线的反向延长线均过像点,因此可以只用任意两条光线就可以确定反射像点的位置. 但是物点发出的单心光束经平面界面折射后不再是严格的单心光束,这时不是任意两条折射光线反向延长的交点都能引起人眼的视觉,要引起人眼视觉,必须有足够强的能量.

以水中物点成像为例,图10中S为物点,水平面为xOz平面,折射光进入人眼成像的光应考虑图中一个微小的立体角内的光束．一直以来人们都只考虑了xOy平面的一个微小平面角内的光,这一微小平面角内的折射光虽然近似反向会聚一点(这个点设为S′,前面用几何画板工具已定量证明,S′偏离y轴距离一般还不小),但其能量相对于总的进入人眼的这个锥体内的光而言,是微乎其微的,是不一定能成像的,除非光锥内的其他折射光也近似反向通过S′点. 光锥与xOy平面内的相截的部分可视为一个椭圆,在椭圆内非x轴上任取一点C,由立体几何知识易知,S′不在SOC平面内,但从C点折射出的光线必在SOC平面内,因此其反向延长线不会严格地通过S′点.倒是可以肯定锥体内的所有折射光线都一定反向通过y轴.由此可以初步发现,最可能成折射像的位置在y轴上.

2.4 平面界面折射像位置的证明

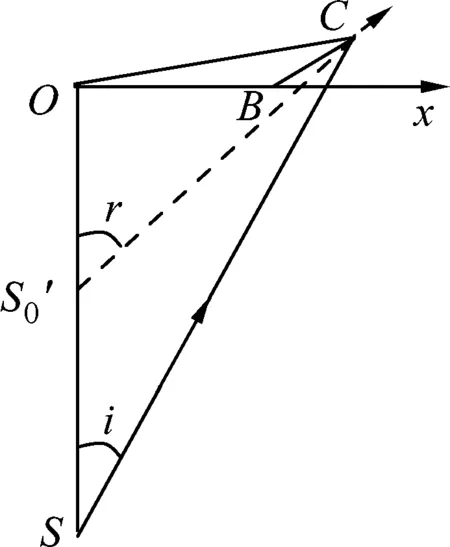
图11

将出射光的椭圆水面按图10的方式细分成许多水带,下面我们证明同一条水带出射的折射光的反向延长线近似地交于y轴上的同一点.考虑正中间的水带,设它的中点B到O的距离为L,物点S到O的距离为h,在水带上取一点C,C到B的距离为Δz,从C点折射出的光线的反向延长线与y轴的交点S0′与O点的距离为h0′,入射角和折射角为i和r,水的折射率为n.结合图11中的几何关系有

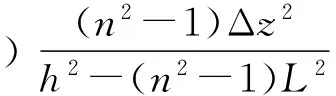
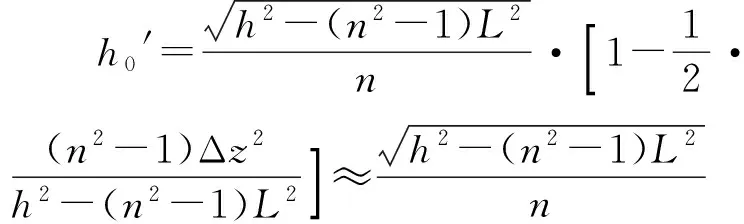
可见,同一水带射出的折射光的反向延长线近似交于y轴上的同一点.对此,我们也可以用数据进行验证,例如,设h=10cm,L=8cm,n=1.33, Δz=0.1cm,代入上面的表达式,可得h0′的精确值为5.35804cm, 近似值为5.35845cm,相差0.00041cm=4.1μm,误差为0.00008,可见近似程度非常高.

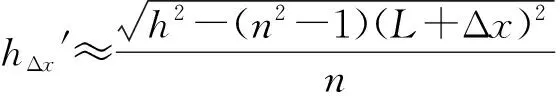
设h=10cm,L=8cm,n=1.33, Δx=0.1cm=1mm,代入上面的表达式,可得hΔx′的值为5.29253cm, 与中心点值(5.35845cm)相差0. 06592cm,误差为1.2%.

3 研究结论

物点经平面界面折射成的像不是严格意义的点像,对于这种非单心光束的像的位置,不能用任意两条光线的反向延长线的交点来确定像的位置,也不能只考查某一微小平面角内的光的反向延长线的交点,而应考虑一个进入人眼的微小立体角的光束的反向交汇点.

物点经过平面界面折射成像的位置在过物点作与界面垂直的线上.在光疏介质中观察时,像相对于物点沿垂线靠近观察者;在光密介质中观察时,像相对于物点沿垂线远离观察者.

1 桂健生.光经平面界面折射成像的位置与观察者方位的关系[J].物理教师,2010(9)：43-44.

2顾敏敏,邱勤薇.平面折射成像究竟在哪儿[J].物理教师,2015(3)：60-61.

2016-08-11)