积分上限函数的导数求法探讨

景慧丽,陈 磊,屈 娜

(火箭军工程大学 理学院, 陕西 西安 710025)

积分上限函数的导数求法探讨

景慧丽,陈 磊,屈 娜

(火箭军工程大学 理学院, 陕西 西安 710025)

积分上限函数的导数的计算是微积分学中的重点和难点，为了帮助学员熟练地掌握积分上限函数的导数求法，对其求导方法进行了探讨.首先定义了标准的积分上限函数，然后给出其求导定理，最后重点探讨了4类非标准型的积分上限函数的导数求法，其基本思想都是化归为标准的积分上限函数.

积分上限函数；导数；化归；高等数学；教学

微积分学的研究对象是函数，因此积分上限函数(也称为变上限的定积分)[1-2]作为一种新型函数在微积分学中的地位是非常重要的.在微积分学中只要是与函数有关的内容，积分上限函数都可以作为一个活跃分子参与其中，如函数的极限运算、函数的导数运算、函数的积分运算、函数的极值和最值运算、微分方程等.在这些运算中，经常要用到积分上限函数的导数，因此，积分上限函数的导数的计算就成了微积分中最重要的内容之一.但是，笔者在教学中发现相当一部分学员往往对求积分上限函数的导数这一问题感到束手无策、无从下手，而且经常出错，从这方面来看，计算积分上限函数的导数又是学员认为的微积分学中最难的知识点之一.为此，笔者对积分上限函数的导数求法进行了探讨，分析、归纳了一般的求法.为了方便说明问题，这里首先要定义一个“标准的积分上限函数”.

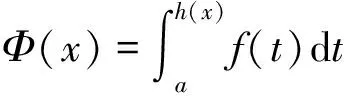
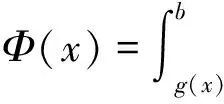
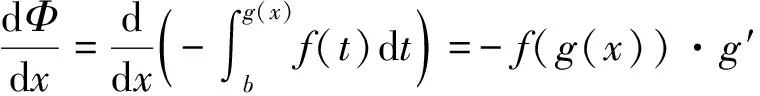
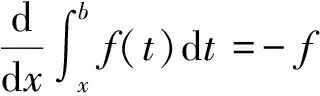
类型4中的被积函数中的自变量x是不能直接和积分变量t分离开的，需要利用定积分的换元积分法把其化归为标准的积分上限函数.

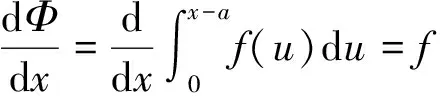
以上就是积分上限函数的求导方法，在所有求法中，最基本、最核心的就是标准的积分上限函数导数的求法，其他非标准的积分上限函数都要先化归为标准的积分上限函数，然后再利用定理.

化归是一种很重要的数学思想方法，化归就是把待解决或未解决的问题，通过转化过程，归结到一类已经解决或者比较容易解决的问题中去，最终求获原问题之解答的一种手段和方法[5].在科学探索中，化归的价值被许多科学家称道，如著名匈牙利数学家路莎·彼得(ROZSA PETER)曾指出：“数学家们往往不是对问题进行正面的攻击，而是不断地将它变形，直至把它转变成已经能够解决的问题.”[5]因此，教员在教学过程中要经常性地让学员体会、感受化归的思想、方法，并培养学员的化归能力.

[1] 同济大学应用数学系.高等数学：上[M].7版.北京：高等教育出版社,2014：238.

[2] 华东师范大学数学系.数学分析：上[M].3版.北京：高等教育出版社,2001：220.

[3] 景慧丽，屈娜，于宁莉，等.积分上限函数的探究式教学[J].河南教育学院学报(自然科学版)，2013,22(1)：54-56.

[4] 姜翠美，姜英，王海霞.变限积分的求导方法[J].高等数学研究，2013,16(6)：23-24.

[5] 熊惠民.数学思想方法通论[M].北京：科学出版社,2010：13-14.

On the Derivative of Integral Upper Limit Function

JING Huili，CHEN Lei, QU Na

(SchoolofNaturalScience,RocketForceUniversityofEngineering,Xi’an710025,China)

Calculating the derivative of integral upper limit function is the important and difficult content of the calculus. The derivative methods of the integral upper limit function were researched，which can help students grasp the derivative methods of the function. First, the standard integral upper limit function was defined, and then the theorem was discussed. Furthermore, the derivative methods of four kinds of non-standard integral upper limit function were particularly and thoroughly researched, and its basic idea is to turn them into the classified as the standard of the integral upper limit function.

integral upper limit function； derivative； transformation and classification; advanced mathematics; teaching

2016-09-18

火箭军工程大学教育教学立项课题(EPGC2015008)

景慧丽(1983—)，女，河南平顶山人，火箭军工程大学理学院副教授，主要研究方向：最优化理论与方法.

10.3969/j.issn.1007-0834.2017.01.013

G642.0;O174

A

1007-0834(2017)01-0059-03