对HB#协议的代数分析
姜 晓, 马昌社
(华南师范大学计算机学院, 广州 510631)
对HB#协议的代数分析
姜 晓, 马昌社*
(华南师范大学计算机学院, 广州 510631)
HB协议是一类对计算要求极低的认证协议,能够抵抗量子攻击,非常适合于移动和物联网环境,而这种无线通信环境要求HB协议应该具有抗中间人攻击的能力. 基于此,设计了一种对HB#协议进行中间人攻击的代数分析方法,在这种代数攻击中,认证密钥可以被快速地恢复. 这一攻击方法建立在Z2中一类多元二次方程组的解的基础之上,首先找到了这类方程组有解的充分必要条件和求解算法,然后利用这一结果对HB#协议进行中间人攻击.
HB协议; 代数攻击; 中间人攻击
LPN(Learning Parity with Noisy)[1]是计算复杂性理论领域内一个研究众多的困难问题,得到了安全界的高度关注. 首先,密码学界基于LPN设计了对称加密[2]、公钥加密[3]等诸多密码方案. 其次,LPN已成为最有可能为计算资源非常有限的设备提供身份识别和认证方案的设计工具[4]. 在这方面,自从HB协议[5]被提出来以后,相继出现了HB+[6]、RANDOM-HB#[7]和Auth[8]等众多基于LPN的认证协议. 这些协议统称为HB类型协议.
由于HB类型协议具有计算要求低和实现代码短的优点,它通常被用来设计RFID(Radio Frequency Identification)认证协议[9-12]. 而RFID系统中标签的被动性、RFID环境的开放性、标签的低成本要求和无线通讯方式给攻击者提供了大量的可用漏洞和资源[13],尤其是给中间人攻击[14]带来了诸多便利条件.
HB协议[5]的执行过程如图1所示. 容易看出HB协议中仅涉及比特加法和乘法,其计算要求非常低. HB协议能够抵御在线窃听等被动攻击,但是无法抵御主动攻击:攻击者只要选择k个线性无关的挑战向量,对每一个挑战向量发起多次主动攻击查询,利用Chernoff定理[3]便可获得其与密钥x的内积,然后用高斯消元法解线性方程组即可得到密钥x.

图1 HB认证协议
HB+协议具有主动安全性[6],但不能抗中间人攻击[14]. RANDOM-HB#协议[7]能抗GRS中间人攻击,但密钥的存储量太大,不符合RFID低成本标签的设计要求,而且不能抵抗一般中间人攻击[15]. 相对于HB+协议和RANDOM-HB#协议的3轮通信,KILTZ等[8]提出2轮认证协议——Auth协议,但Auth协议仍然无法抵抗中间人攻击[16].
在抗中间人攻击研究方面,KILTZ等[8]提出了基于LPN的MAC(Message Authentication Code),此协议能够抗一般中间人攻击,但需要用到两两独立的置换,超出了LPN的范围[17]. 最近,唐静和姬东耀[18]提出一个基于LPN的抗中间人攻击的认证协议HB#,但本文将分析其仍然不能抵抗中间人攻击.
由于LPN问题呈现出良好的线性代数特性,导致其容易遭受代数攻击[19]. 本文采用代数攻击方法对HB#协议进行攻击,将密码体制的加密活动描述为输入(密钥)和输出之间的多元方程组,并且通过求解方程组来恢复密钥. 每个密码都可以描述为Z2上的多元方程组[20],而解Z2上的非线性多元方程组的问题通常都是NP问题[20-21]. 因此,要想对某个安全方案进行代数分析,首先要找到该安全方案对应的多元非线性方程组的求解方法. 本文首先对Z2中一类多元二次方程组进行研究,给出其求解算法及该方程组有解的充分必要条件;然后利用GRS攻击原理[14]设计了对HB#协议[18]的中间人攻击算法,在该算法中,把认证密钥的恢复归约到这一方程组的求解,完成对HB#协议的中间人攻击.
1 预备知识
1.1 符号说明
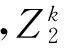
1.2 LPN问题

1.3 环排列
把k个不同的元素按照圆圈排列,这种排列叫做环排列[22]. 2个环排列是同一排列,若环排列中同一元素的左右邻居没有改变. 由(c0,c1,c2,…,ck-1)组成的环排列(图2)易知,由k个不同元素组成的环排列共有(k-1)!个.
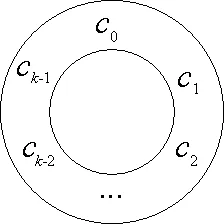
图2 环排列(c0,c1,c2,…,ck-1)
2 HB# 协议
为了解决HB协议不能抵御主动攻击的问题,JUELS和WEIS[6]设计了HB+协议. 与HB协议的2轮认证不同的是,HB+协议中阅读器与标签之间增加了另外一个共享的k比特密钥y,HB+协议中需要标签首先产生k比特向量b发给阅读器,并把b加入到验证值z的计算中,即z=a·xb·yv. 正是b的随机性使得攻击者无法利用主动攻击得到密钥,这样HB+协议实现了主动安全性. 但是HB+协议仍然无法抵御中间人攻击:文献[14]提出的一种中间人攻击的方法(简称GRS攻击),成功地对HB+协议进行了中间人攻击. GRS攻击原理为:攻击者通过“拦截消息-修改消息-发送消息”的方式[14]对阅读器和标签之间的通信进行干预,同时需要构建一些参数使认证通过,从而获得所需要的信息,这样经过多次攻击之后攻击者能够成功恢复出密钥. 下面具体阐述对HB+协议的GRS攻击.
针对HB+协议,攻击者伪装成合法的标签,截获每次阅读器发送的a,通过异或上同一个k比特向量б将a篡改为a′=aб;攻击者再伪装成合法的阅读器将a发送给标签;阅读器按照HB+协议验证a·xb·y=z是否成立. 整个攻击过程中,攻击者通过选择合适的б(比如б=(1,0,…,0)),通过一个完整的认证协议执行过程,根据认证结果即可恢复出密钥x的第一个比特,重复这个过程k次就可以恢复出密钥x的所有比特. 具体的GRS中间人攻击如图3所示.
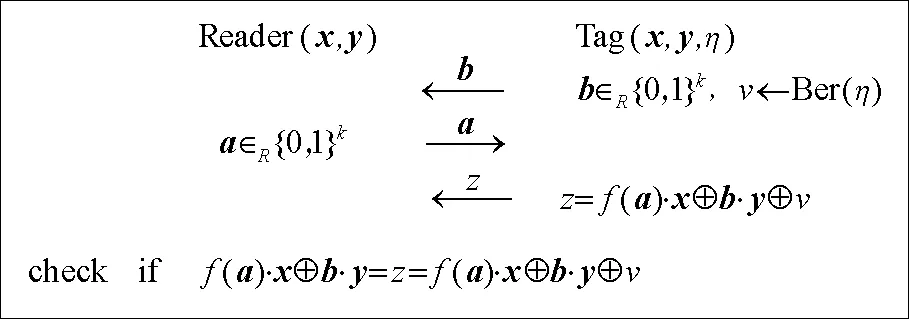
图3 GRS攻击
针对HB+协议不能抵抗中间人攻击的问题,唐静和姬东耀[18]提出了宣称能够抵抗中间人攻击的HB#协议. 与HB+协议不同的是,HB#协议中标签端先对挑战消息a进行一次非线性运算f,然后再按HB+的方式产生认证码z. 本文研究发现文献[18]提出的改进方法仍不能抵抗中间人攻击.
具体的HB#协议为:阅读器与标签共享2个k比特密钥x=(x0,x1,…,xk-1)和k比特密钥y=(y0,y1,y2,…,yk-1). 标签拥有1个噪声发生器,以ηa(0,1/2)的概率生成噪声v(即Pr[v=1]=η). 1个完整的HB#协议包括r次协议执行,在1次协议中,标签随机生成k比特向量b并发送其给阅读器. 阅读器收到后随机生成k比特向量a并发送其给标签. 标签计算验证码z=f(a)·x(b·y)v然后发送z给阅读器,阅读器检验f(a)·x(b·y)v=z是否成立. 这样进行r次交互后,如果标签响应错误的次数小于某个阀值ω,则认证通过. HB#认证协议的具体流程如图4所示,其中f是一个非线性函数,假设k比特向量则f(a)=f(a0,a1,…,ak-2,ak-1)=(a0a1,a1a2,…,ak-2ak-1,ak-1a0).
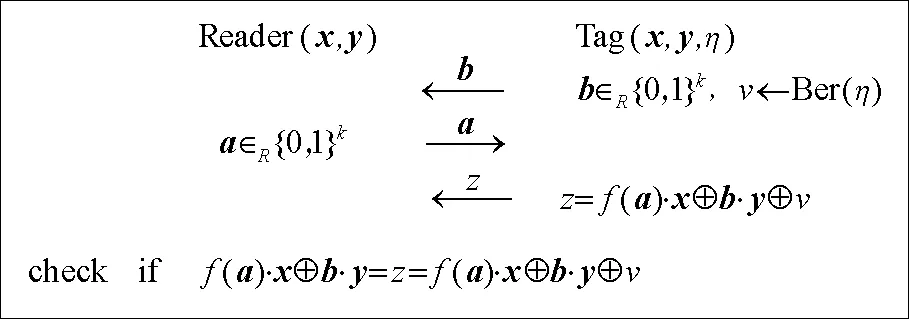
图4 HB#认证协议
3 HB# 协议中间人攻击
3.1 HB#协议中间人攻击原理
在HB#协议中,对挑战消息a进行线性篡改(把a改成aб)后把f(aб)拆分成f(a)+g(a,б)的形式,然后利用阅读器,攻击者就可以获得g(a,б)与标签密钥的内积,重复这一过程多次,可以建立以标签密钥为未知数的方程组,解方程组就可以得到标签密钥,从而完成中间人攻击.
具体来讲,攻击者伪装成一个合法的标签,截获每一次阅读器发送的a,异或上一个k比特向量б,然后伪装成合法的阅读器将a′=aб发送给标签. 标签收到后计算z=f(a′)·xb·yv并将z发回去,阅读器检验是否f(a)·xb·y=z.
每次认证中阅读器给出的a是随机的,要求攻击者每次通过选取б来消除由a带来的差异,使得多次认证中f(aб)-f(a)的结果以较大概率相同. 定义函数g(a,б)=f(aб)-f(a),则标签计算
z=f(a′)·xb·yv=f(aб)·xb·yv=f(a)·xb·yg(a,б)·xv.
而阅读器可以帮助攻击者验证f(a)·xg(a,б)·xv,从而获得g(a,б)·xv的值,则攻击者经过多次攻击就可以以很大概率获得g(a,б)·x的值,进一步根据r次交互认证的认证结果恢复密钥x. HB#协议的中间人攻击过程如图5所示.

图5 HB#协议的中间人攻击
3.2 HB#协议中间人攻击实施
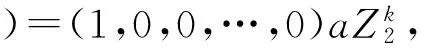
z=f(a′)·x(b·y)v=f(a)·x(b·y)g(a, б)·xv=f(a)·x(b·y)(1,0,0,…,0)·(x0,x1,x2,…,xk-1)v=f(a)·x(b·y)x0v.
r次交互以后,如果标签认证通过则设置x0=0,否则x0=1. 同样的方法,攻击者在接下来的攻击中选择б满足f(aб)=f(a)+(0,1,0,…,0)即可判断x1的值. 最后攻击者选择б满足f(aб即可判断出xk-1的值,这样,攻击者就成功恢复密钥x.
攻击者得到密钥x后可以成功冒充标签与阅读器进行通信,有2种方式:
(1)无需恢复密钥y:鉴于HB#协议中b由标签给定,因此攻击者可以每次设定b=(b0,b1,b2,…,bk-1)=(0,0,0,…,0),则由攻击者发送给阅读器的z值为:z=f(a)·x(0,0,0,…,0)·yv=f(a)·xv. 这样进行r次后,如果阅读器收到错误响应的次数小于ω,则攻击者冒充标签成功. 攻击者冒充标签的攻击过程如图6所示.

图6 标签冒充攻击
(2)选取k个线性无关的向量b,根据认证结果构成线性方程组,用高斯消元法解矩阵方程恢复密钥y:HB#协议中密钥y表示为y=(y0,y1,y2,…,yk-1),攻击者首先选取b=(b0,b1,b2,…,bk-1)=(1,0,0,…,0),则攻击者计算z=f(a)·x(1,0,0,…,0)·(y0,y1,y2,…,yk-1)v=f(a)·xy0v,保持b不变,攻击者与阅读器进行r次交互,并将r次认证后阅读器对攻击者的认证结果记为d0(若认证通过d0=0,否则d0=1). 同样的方法,攻击者选取b=(0,1,0,…,0),则计算z=f(a)·x(0,1,0,…,0)·(y0,y1,y2,…,yk-1)v=f(a)·xy1v,重复进行r次,并将阅读器对攻击者的认证结果记为d1. 最后选取b=(0,0,0,…,1),并将阅读器对攻击者的认证结果记为dk-1. 易知,密钥y=(d0,d1,d2,…,dk-1),即攻击者成功恢复密钥y.
3.3 HB#中间人攻击算法的分析
首先考虑一类Z2上多元二次方程组的解. 设u0,u1,…,uk-1aZ2为未知数,c0,c1,c2,…,ck-1äZ2为已知数. 关于u0,u1,…,uk-1的二次方程组为:
(1)
一般地,求解Z2的多元二次方程组是一个NP困难问题[16-17],但对于某些特殊方程组可以快速求解. 关于方程组(1)求解的情况如引理1所述:
引理1 方程组(1)有解的充要条件是:环排列(c0,c1,c2,…,ck-1)中不含有子串“101”.
证明 必要性:已知方程组(1)有解,将证明环排列(c0,c1,c2,…,ck-1)中不含有子串“101”.

由uiui+1=1可得ui=ui+1=1;由ui+2ui+3=1可得ui+2=ui+3=1. 据此ui+1ui+2≠0,即不存在ui、ui+1、ui+2和ui+3满足uiui+1=1、ui+2ui+3=1且ui+1ui+2=0,故方程组(1)无解.
充分性:已知环排列(c0,c1,c2,…,ck-1)中不含有子串“101”,接下来将证明方程组(1)有解. 求出方程组(1)的一个解的多项式时间算法如下:
for(i=1;i≤k;i++)
if(ci==1) then
ui=ui+1=1;
elseui+1=0.
算法的正确性分析:如果当前i满足ci=1,由uiu(i+1)mod k=1可知ui=u(i+1)mod k=1;如果ci=0,由于环排列(c0,c1,c2,…,ck-1)中不含有子串“101”,则c(i+1)mod k=0或者c(i-1)mod k=0. 此时可选取ui=0以同时满足ui-1ui=uiu(i+1)mod k=0. 而根据方程组(1)的多项式时间求解算法可知ui在第i-1次时已被设置为0,因此只需考虑c(i+1)mod k=0的情形,此时选择u(i+1)mod k=0即可满足. 从而按照方程组(1)的多项式时间求解算法可以得到方程组(1)的一个解(当环排列(c0,c1,c2,…,ck-1)中含有3个或3个以上连续的0时,方程组(1)有多个解,通过排列组合的方式可得到全部解,此处选择其中的一个解). 关于算法的时间复杂度,由于算法总共进行了k次比较,因此时间复杂度是O(k),为多项式时间复杂度.
其次,从3.2节可以看出,只要б存在,那么通过篡改a并利用认证结果就可以恢复标签密钥x. 下面将分析б存在的概率和恢复x的概率. 这里先分析б存在的概率,具体如引理2所示:

证明 由引理1易知,f(a)=(c0,c1,c2,…,ck-1)所组成的环排列中不含有子串“101”,其中ci=aiai+1. 由引理1知,只要f(a)+(0,…,0,1,0,…,0)不含有子串“101”,那么必然存在б满足f(aб)=f(a)+(0,…,0,1,0,…,0),而f(a)+(0,…,0,1,0,…,0)中子串“101”只可能存在于以第i个位置为中心的5个连续的位置,因此需要考虑(ci-2,ci-1,ci,ci+1,ci+2)+(0,0,1,0,0)中出现子串“101”的情况, 其中ci-2、ci-1、ci、ci+1、ci+2由ai-2、ai-1、ai、ai+1、ai+2、ai+3决定. 经计算发现,当ai-2、ai-1、ai、ai+1、ai+2、ai+3属于(***011)、(*1111*)和(110***)这3种形式的向量时,(ci-2,ci-1,ci,ci+1,ci+2)+(0,0,1,0,0)中一定会出现子串“101”. 于是,共有23+22+23-1=19种情况使得引理2的方程无解,则方程f(aб)-f(a)=(0,…,0,1,0,…,0)有解的概率为(26-19)/26=45/64.
接下来将给出攻击者在一次攻击中恢复密钥x的一个比特xi的概率.

证明 根据xi取值分2种情况:(1)当xi=0时,z=f(a)·xb·yxiv=f(a)·xb·yv,即攻击者对a的篡改不改变标签的认证码z,从而不改变阅读器对标签的认证结果,于是标签可以通过阅读器认证. 根据3.2节的攻击算法,攻击者以概率1的优势恢复出xi=0. (2)当xi=1时,z=f(a)·xb·yxiv,在这种情况下将证明阅读器以压倒性的概率拒绝标签:由引理2得知,攻击者对a篡改成功的概率为45/64,则z=f(a)·xb·yv,其中是一个参数为45/64的贝努利随机变量. 易知,v仍服从贝努利分布,设其参数为α,则从而得到一个参数α>1/2的HB#认证协议. 进一步由Chernoff定理[3]可得:HB#中间人攻击中标签响应错误的次数大于ω的概率至少为1-e-θ2αr/3,其中0<θ<(α-η)/α.
以下定理将给出3.2节的中间人攻击算法中攻击者恢复密钥x的概率.
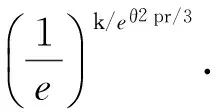

4 结束语
LPN不但可以为RFID系统提供低成本的认证协议,而且还可以抵抗量子攻击. 自从首个基于LPN的HB协议在2001年提出来以后,相继出现了众多的HB类型协议. 这些协议绝大部分不能抵抗中间人攻击,一小部分只能抗主动攻击,大部分可以抵抗被动攻击. HB类型协议的发展还是遵循着协议设计、协议分析、协议改进这样一条循环前进的道路,少有HB类型协议具有可证明的安全性. 而LPN假设自身的简单性与线性特点给认证协议的设计带来极大的困难,因此基于LPN设计出实用的、可证明安全的认证协议仍是HB类型协议发展的主要方向. 该文在研究一类多元二次方程组的解的基础上,对HB#协议进行了中间人攻击,攻击算法的复杂度低且成功概率高. 这里提出的多元二次方程组的解不但可以用在HB类型协议的代数攻击上,而且有望用于其他协议的分析,为进一步设计安全的HB类型协议提供了指导.
[1] BLUM A,KALAI A,WASSERMAN H. Noise-tolerant learning,the parity problem,and the statistical query model[J]. Jounal of ACM,2003,50(4):506-519.
[2] GILBERT H,ROBSHAW M J B,SEURIN Y. How to encrypt with the LPN problem[C]∥ACETO L,DAMGÅRD L A,GOLDBERG L A,et al. Automata,Languages and Pro-gramming. Berlin:Springer,2008:679-690.[3] KILTZ E,MASN D,PIERTRZAK K. Simple chosen-ciphertext security from low-noise LPN[C]∥KRAWCZYK H. Public-Key Cryptography-PKC 2014. Berlin:Springer,2014:1-18.
[4] GUO Q,JOHANSSON T,LONDAHL C. Solving LPN using covering codes[C]∥SARKAR P,IWATA T. Advances in Cryptology-ASIACRYPT 2014. Berlin:Springer,2014:1-20.
[5] HOPPER N J,BLUM M. Secure human identification protocol[C]∥BOYD C. Advances in Cryptology-ASIACRYPT. Berlin:Springer,2001:52-66.
[6] JUELS A,WEIS S. Authenticating pervasive devices with human protocols[C]∥SHOUP V. Advances in Cryptology-CRYPTO 2005. Berlin:Springer,2005:293-308.
[7] GILBERT H,ROBSHAW M,SEURIN Y. HB#:increasing the security and efficiency of HB+[C]∥SMART N. Advances in Cryptology-EUROCRYPT 2008. Berlin:Springer,2008:361-378.
[8] KILTZ E,PIETRZAK K,CASH D,et al. Efficient authentication from hard learning problems[C]∥PATERSONK G. Advances in Cryptology- EUROCRYPT 2011. Berlin:Springer,2011:7-26.
[9] 周世杰,张文清,罗嘉庆. 射频识别(RFID)隐私保护技术综述[J]. 软件学报,2015,26(4):960-976.
ZHOU S J,ZHANG W Q,LUO J Q. Survey of privacy of radio frequency identification technology[J]. Journal of Software,2015,26(4):960-976.
[10] 马昌社. 前向隐私安全的低成本RFID认证协议[J]. 计算机学报,2011,34(8):1387-1398.
MA C S. Low cost RFID authentication protocol with forward privacy[J]. Chinese Journal of Computer,2011,34(8):1387-1398.
[11]LI Y J,DENG R H,LAI J Z,et al. On two RFID privacy notions and their relations[J]. ACM Transaction on Information and System Security,2011,14(4):68-85.
[12]MA C S,WENG J. Radio frequency identification system security proceedings of rfidsec asia workshop[M]. Netherlands:IOS Press,2013.
[13]AVOINE G,COISEL I,MARTIN T. Untraceability model for RFID[J]. IEEE Transactions on Mobile Computing,2014,13(10):2397-2405.
[14]GILBERT H,ROBSHAW M,SILBERT H. Active attack against HB+:a provably secure lightweight authentication protocol[J]. Electronics Letters,2005,41(21):1170.
[15]OUAFI K,OVERBACK R,VAUDENAY S. On the security of HB#against a man-in-the-middle attack[C]∥PIEPRZYK J. Advances in Cryptology-ASIACRYPT 2008. Berlin:Springer,2008:108-124.
[16]KOSEI E,NOBORU K. Security analysis on AUTH protocol and its variant against the man-in-the-middle attack[J]. IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences,2015,98(1):153-161.
[17]LYUBASHEVSKY V,MANSY D. Man-in-the-middle secure authentication schemes from LPN and weak PRFs[C]∥CANETTI R,GARAY J A. Advances in Cryptology-CRYPTO 2013. Berlin:Springer,2013:308-325.
[18] 唐静,姬东耀. 基于LPN问题的RFID安全协议设计与分析[J]. 电子与信息学报,2009,31(2):439-443.
TANG J,JI D Y. Design and analysis of security protocol for RFID based on LPN problem[J]. Journal of Electronics& Information Technology,2009,31(2):439-443.
[19]COURTOIS N T,MEIER W. Algebraic attacks on stream ciphers with linear feedback[C]∥BIHAM E. Advances in Cryptology-EUROCRYPT 2003. Berlin:Springer,2003:345-359 .
[20]COURTOIS N,KILMOV A,PATARIN J,et al. Efficient algorithms for solving overdefined systems of multivariate polynomial equations[C]∥PRENEEL B. Advances in Cryptology-EUROCRYPT 2000. Berlin:Springer,2000:392-407.
[21]BLUM A,FURST M,KEARNS M,et al. Cryptographic primitives based on hard learning problems[C]∥STINSON D R. Advances in Cryptology-CRYPTO’ 93. Berlin:Springer,1993:278-291.
[22]BRUALDI R A,FENG S. Introductory combinatorics[M]. Beijing:China Machine Press,2012:53-56.
【中文责编:庄晓琼 英文审校:肖菁】
Algebraic Analysis on HB#Authentication Protocol
JIANG Xiao, MA Changshe*
(School of Computer Science, South China Normal University, Guangzhou 510631,China)
HB-like protocols are such a kind of authentication protocols that require low computational resource and promise to resist quantum attacks. They are especially suitable for mobile applications and the Internet of Things (IoT). However, the wireless communications in these environments have compelled that HB-like protocols should be able to resist the man-in-the-middle (MIM) attacks. In this vein, this paper proposes an algebraic MIM attack to a recently presented HB#authentication protocol which is claimed to resist MIM attacks. During this attack, the authentication keys can be totally recovered efficiently. The proposed attacking method is based on the solutions to a system of quadratic equations of multi-variables overZ2. Hence, the necessary and sufficient conditions for this system of equations being solvable have been found in advance. Then, an algebraic attack to HB#protocol has been presented accordingly.
HB protocol; algebraic attacks; man-in-the-middle attack
2015-08-04 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
国家自然科学基金项目(61672243);广东省自然科学基金项目(S2013020011913);广东省教育厅科技创新项目(2013KJCX0055);广州市基础研究项目(11C42090777)
TP309
A
1000-5463(2017)01-0110-06
*通讯作者:马昌社,教授,Email:chsma@163.com.

