基于路网客流模态的城市轨道交通网络拥堵演变机理

李 曼 王艳辉 晋 君 贾利民

(1北京交通大学轨道交通控制与安全国家重点实验室, 北京 100044)(2北京交通大学交通运输学院, 北京 100044)

基于路网客流模态的城市轨道交通网络拥堵演变机理

李 曼 王艳辉 晋 君 贾利民

(1北京交通大学轨道交通控制与安全国家重点实验室, 北京 100044)(2北京交通大学交通运输学院, 北京 100044)

为描述客流负荷状态及拥堵演变规律,基于客流梯度概念提出了路网客流模态概念及其物理特征描述,包括自由模态、拥堵模态和拥堵消散模态．采用客流场强的计算公式来估算下车客流比例,将车站客流负荷指数和区段客流负荷指数作为点拥堵的关键参数,计算路网客流模态值．提出成网运营条件下的客流交换关键参数,并构建基于元胞自动机模型的客流拥堵动态演变模型,研究路网客流拥堵的动态传播与演变规律,分析路网客流群体行为演化机理．以北京市部分城市轨道交通路网为例,基于客流实际调查数据,通过调整上车客流比例,利用MATLAB软件对不同时刻的路网客流模态值进行仿真计算．结果表明,不同时段内路网客流处于不同模态,从而验证了路网客流模态的物理特征．

城市轨道交通;客流模态;客流场强;拥堵演变;元胞自动机模型

城市轨道交通路网规模的扩大、客流负荷量的提高以及路网客流拥堵现象的产生,使得路网运营安全管理工作难度不断增大．如何揭示隐藏在路网客流拥堵现象背后的机理、减少拥堵线路对其他线路的影响、避免客流在网络中某一个节点阻塞而造成整个网络运输效率降低,是运营安全管理工作中迫切需要解决的关键问题．

目前,国内外学者已对城市轨道交通网络客流拥堵机理与传播模型进行了相关研究．骆晨等[1]基于网络拥挤模型建立了超大客流拥堵网络疾病传播模型;李朴[2]建立了客流拥堵传播SIR模型,并对不同性质及初始多发站发生的客流拥堵情况进行模拟仿真;曹志超[3]提出了无约束的突发大客流演化模型,对其在网络中的演化过程进行仿真．除城市轨道交通外,关于网络流的动态演化与拥堵传播的研究较多集中于道路网络交通流领域,使用的方法论主要基于元胞自动机模型[4-5]等．针对城市轨道交通网络客流分布特征的分析,主要关注城市轨道交通路网的网络特性[6-8]、客流不均衡性与客流空间分布[9]等．在客流演化研究方面,相关学者通过不同模型算法分析了客流的演化过程[10-11]．由此可知,客流行为与客流演化仿真模型的研究对象多集中在单个车站内部或应急疏散过程或单条线路．应用SIR理论研究客流拥堵传播模型的文献较多,然而定量描述路网区域客流拥堵、将点拥堵(车站、区段的客流超负荷状态)作为模型中的关键因素来揭示客流拥堵演化机理的研究较为匮乏,同时,将上下车客流数据考虑到网络客流拥堵模型中进行深入分析的研究也相对较少．

为描述路网中区域拥堵现象,基于车站、区段客流负荷指数即点拥堵指标,提出了路网客流拥堵模态的概念与模态特征．因较难获取上下车客流的实际数据,本文利用客流场强的计算公式来描述不同车站的客流吸引强度,近似估计下车客流数据．为分析路网中的拥堵传播机理,基于元胞自动机建立了路网客流拥堵演化模型．当模型内上车客流比例出现变化时,通过调整限流措施改变点拥堵状态变量,使路网客流模态处于较安全的范围内．

1 基于运营安全参数的路网客流模态

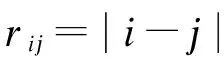
1.1 点拥堵

1.1.1 车站站台客流负荷指数

作为描述车站客流拥堵状态的主要依据,t时刻车站Si的站台客流负荷指数的计算公式为

参照车站站台等候区服务水平标准对乘客各感知状态的划分以及对实际调研数据的聚类分析,将城市轨道交通车站客流负荷水平状态划分成不同等级,结果见表1．

表1 城市轨道交通车站站台客流负荷指数

1.1.2 区段客流负荷指数

区段客流负荷指数Lt(l)表示一定时间内区段l的列车运载乘客的平均满载程度,反映了区段客流拥堵状态,具体表达式为

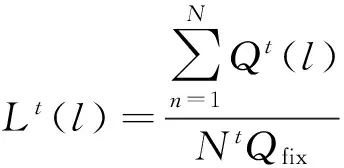
参照《城市轨道交通安全运营管理办法》及对实际调研数据的聚类分析,将城市轨道交通区段列车客流负荷水平状态划分成不同等级,结果见表2．

表2 城市轨道交通区段列车客流负荷水平

1.2 基于点拥堵的路网客流模态

鉴于客观存在的空间差异,路网中车站客流承载量各不相同,客流承载量相对较大的车站(简称中心站)附近的邻居车站客流量也较大．客流作为路网的主要流动介质,与出行车站之间的吸引作用所形成的场域称为客流场[12-13]．客流场强表示中心站对场内某点提供的客流下车能力．

客流梯度沿不同方向衰减传播的表达式为

式中

式中,Q为路网中某中心站的站台到达候车客流;Q1为客流梯度沿p1方向的衰减量;k1,k2,…,kn为不同方向p1,p2,…,pn对应的相关参数．

由此可知,随着空间距离的增加,中心站向四周场强逐渐衰减,直到接近另一个中心站,场强才开始增强．沿等客流面切向,客流强度不变;沿垂直于等客流面的法向,客流强度变化率最大．

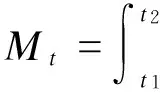
以路网客流系统中点拥堵的关键参数为基础,根据拥堵发生区域和产生规模,建立路网客流模态集并给出模态的物理特征描述,结果见表3．

表3 路网客流模态集

2 城市轨道交通路网客流模态演变机理

2.1 成网运营条件下的客流交换关键参数

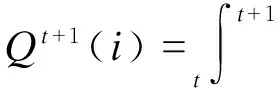
2.2 基于元胞自动机模型的客流拥堵动态演变模型

元胞自动机是指定义在一个由具有离散、有限状态的元胞组成的元胞空间上,按照一定的局部规则在离散时间维度上演化的动力系统[15]．

构建模型之前,首先给出以下3个假设条件:① 对车站客流负荷状态的描述应包含车站中所有内部设施拥挤状态,但考虑到客流在路网中的拥堵传播,这里简化为仅考虑站台客流负荷状态;② 以实际发车间隔为元胞演化的时间步长;③ 只考虑单方向的列车运营情况．

关于模型参数进行以下几点说明:① 元胞分为车站元胞和区段元胞．选取元胞半径r=1．对于换乘车站元胞,即某一个车站衔接2条及以上线路,采用Moore型邻居形式．② 分别根据站台客流负荷指数Pt(i)和区段列车负荷指数Lt(l)定量划分车站元胞的客流状态空间C(i)={0,1,2,3}和区段元胞的客流状态空间C(l)={0,1,2}．③ 由于车站的客流变化是与列车到站进行客流交换产生的,研究拥堵状态的传播需满足Δt≥t2-t1．其中,Δt为演化时间.

对客流的单个周期进行分析．根据每次客流交换确定车站和区段列车客流相应的演化规则,建立基于CA的客流拥堵动态演变模型．该模型建立在二维规则的元胞自动机网格上,采用Moore邻居模型和周期循环边界条件．

车站i元胞客流量演化规则可表示为

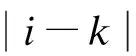
结合2.1节中的客流交换关键参数,则有

相邻车站Si上区段列车l的元胞客流量演化规则为

根据2.1节中的客流交换关键参数可得

依据基于元胞自动机模型的演化规则推导车站和区段元胞下一时刻的客流量,并分别依据车站客流密度Pt(i)和区间客流负荷指数Lt(l)计算车站和区段列车在不同时刻的客流负荷等级水平．通过分析不同时刻的路网客流拥堵规模,定量刻画路网客流模态,研究路网客流模态的演变机理．

3 实例仿真

3.1 客流模态演变

选取北京市地铁1号线(东单至军事博物馆S1→S9)和4号线(动物园至陶然亭S10→S18)组成的部分网络,车站Si→Sj之间的区段表示为Li,j．以2015年8月10日06∶00—20∶00的客流数据为研究对象,根据客流调查,按照列车下行方向,获得客流到达站台率．由于站台运营性质及设计不同,各车站站台面积也各不相同,根据车站日均客流量和高峰小时客流量对车站站台进行分类．假设列车在相邻车站之间的平均运行时间间隔为2 min,列车的定员数为1 900人,最大运载能力为2 600人,密集区客流与非密集区客流的比例为8∶2．基于元胞自动机模型,假设06∶00为列车的初始运营时刻,以2 min为单位演化时间．设定不同上车客流比例,运用MATLAB软件对路网客流模态演化过程进行仿真．

描述路网客流模态特征时,根据站台客流负荷指数Pt(i)和区段列车负荷指数Lt(l)获得各元胞的状态值,以表达路网整体的客流演变过程．图1给出了ω=0.8时不同时刻路网客流状态的元胞表现形式．图中,灰色区域表示客流负荷值尚未到达拥堵临界点,即C(i)={0,1},C(l)={0,1};红色区域表示客流负荷已经达到拥堵状态,即C(i)≥2,C(l)=2．

3.2 结果分析

分别对ω=1.0,0.8,0.6,0.4时的情况进行仿真,依据演化结果对路网客流模态值M进行求解,其公式为

(5)

式中,nu为线路u中元胞状态为红色的元胞个数;Nline,u为线路u元胞总数;lu为线路u连续拥堵的元胞个数,即当线路中连续若干元胞均为红色时的连续拥堵长度;Lline,u为线路u最大直径距离上的元胞总数(包含车站和区段元胞);qv为区域拥堵指数,以换乘站及其邻居状态为出发点,若换乘站v的所有邻居元胞状态均为红色,则qv=1,否则qv=0．

(a) 06∶20

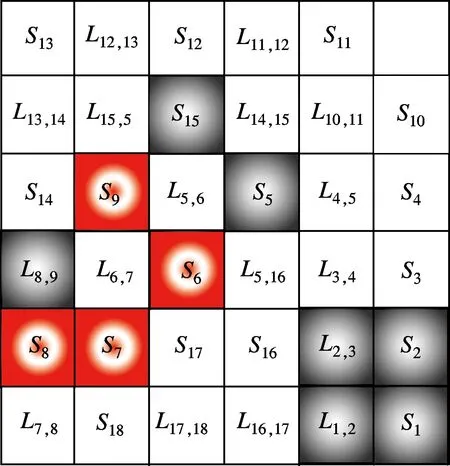
(b) 07∶30

(c) 08∶40

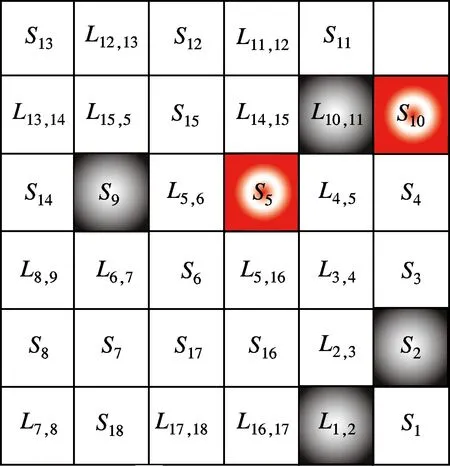
(d) 12∶40

(e) 17∶40

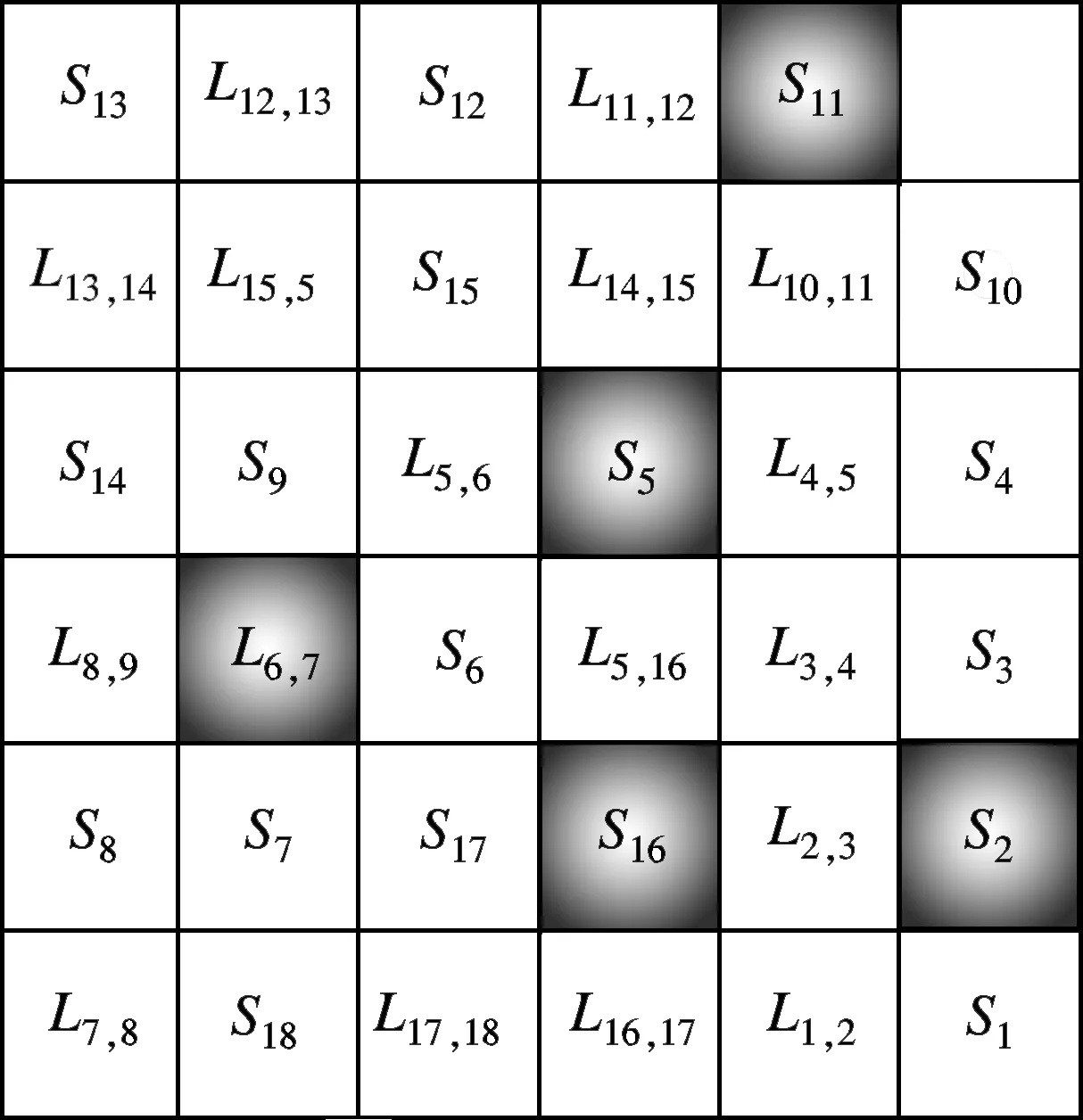
(f) 20∶00

实例计算结果见表4．由表可知,对于部分车站或区段,ω不同导致达到点拥堵临界点的时间不同．对于平峰期,ω越高,其路网客流空间拥堵规模越小;对于高峰期,随着站台客流到达率增加,ω越低,点拥堵规模越大．

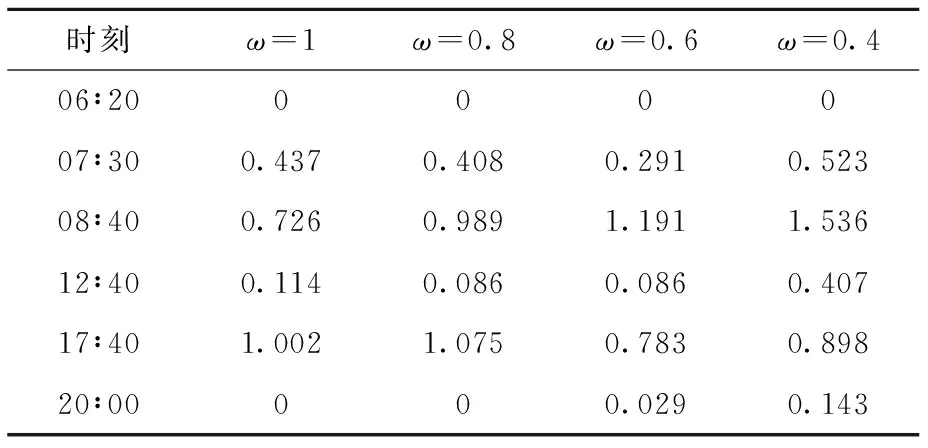
表4 不同时刻不同上车客流比例下的路网客流模态值

通过与地铁相关运营公司的调研与沟通,确定M=0.4为拥堵模态的跃迁阈值点,分析表4结果可得不同时段的路网客流模态(见表5)．

表5 路网客流模态的时间分布

4 结语

以路网客流梯度为出发点,定义了路网客流模态及3种模态的物理特征,分析了客流交换过程中的关键参数.以车站和区段为2类元胞,基于元胞自动机模型定义相应的客流演化规则,建立基于点拥堵的客流拥堵动态演变模型,研究模态演变机理与传播规律．以北京市城市轨道交通部分路网为例,结合实际调查的客流数据,对模型进行仿真．结果显示,不同时刻下路网客流拥堵模态规模不同．尽管上车客流比例ω不同,但相同时段路网客流模态特征是统一的．对于部分车站或区段,ω不同导致达到点拥堵临界点的时间不同．对于平峰期,ω越高,其路网客流空间拥堵规模越小;对于高峰期,随着站台客流到达率增加,ω越低,点拥堵规模越大．下一步研究工作包括双方向的路网客流状态元胞演化规则及模型中下车客流变量参数的优化．

References)

[1]骆晨, 刘澜, 牛龙飞. 城市轨道交通超大客流网络拥挤传播研究[J]. 石家庄铁道大学学报(自然科学版), 2014, 27(2): 83-86. DOI:10.13319/j.cnki.sjztddxxbzrb.2014.02.18. Luo Chen, Liu Lan, Niu Longfei. The research on the network congestion for large passenger flow of urban rail transit[J].JournalofShijiazhuangTiedaoUniversity(NaturalScienceEdition), 2014, 27(2): 83-86. DOI:10.13319/j.cnki.sjztddxxbzrb.2014.02.18.(in Chinese)

[2]李朴.城市轨道交通运营网络客流分布特性及客流拥堵传播规律研究[D]. 北京:北京交通大学交通运输学院, 2012.

[3]曹志超.网络条件下城市轨道交通突发大客流演化机理和应急策略研究[D]. 北京:北京交通大学交通运输学院,2013.

[4]Gao Z Y, Li K P, Li X G, et al. Scaling laws of the network traffic flow[J].PhysicaA:StatisticalMechanicsanditsApplications, 2007, 380: 577-584. DOI:10.1016/j.physa.2007.02.036.

[5]Li K P, Gao Z Y. A topological approach to traffic dynamics[J].EurophysicsLetters(EPL), 2006, 74(2): 369-375. DOI:10.1209/epl/i2005-10524-1.

[6]Zhang J, Xu X, Hong L, et al. Networked analysis of the Shanghai subway network, in China[J].PhysicaA:StatisticalMechanicsanditsApplications, 2011, 390(23/24): 4562-4570. DOI:10.1016/j.physa.2011.06.022.

[7]Zhang J, Zhao M, Liu H, et al. Networked characteristics of the urban rail transit networks[J].PhysicaA:StatisticalMechanicsanditsApplications, 2013, 392(6): 1538-1546. DOI:10.1016/j.physa.2012.11.036.

[8]Derrible S, Kennedy C. The complexity and robustness of metro networks[J].PhysicaA:StatisticalMechanicsanditsApplications, 2010, 389(17): 3678-3691. DOI:10.1016/j.physa.2010.04.008.

[9]尚斌, 张小宁. 城市轨道交通客流空间分布模型[J]. 西南交通大学学报, 2013, 48(3): 539-545. DOI:10.3969/j.issn.0258-2724.2013.03.023. Shang Bin, Zhang Xiaoning. Passenger-flow spatial distribution model of urban rail transit[J].JournalofSouthwestJiaotongUniversity, 2013, 48(3): 539-545. DOI:10.3969/j.issn.0258-2724.2013.03.023.(in Chinese)

[10]李曼, 王艳辉, 贾利民. 城市轨道交通车站客流模态与控制策略[J]. 东南大学学报(自然科学版), 2015, 45(6): 1203-1208. DOI:10.3969/j.issn.1001-0505.2015.06.032. Li Man, Wang Yanhui, Jia Limin. Passenger flow modes and control strategies in urban rail transit station[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2015, 45(6): 1203-1208. DOI:10.3969/j.issn.1001-0505.2015.06.032.(in Chinese)

[11]Shi C, Zhong M, Nong X, et al. Modeling and safety strategy of passenger evacuation in a metro station in China[J].SafetyScience, 2012, 50(5): 1319-1332. DOI:10.1016/j.ssci.2010.07.017.

[12]晋君.城市轨道交通路网运营客流模态演变机理研究[D].北京:北京交通大学交通运输学院,2015.

[13]邓润飞, 过秀成. 基于场论的空间客运联系特性与建模分析[J]. 东南大学学报(自然科学版), 2015, 45(1): 178-183. DOI:10.3969/j.issn.1001-0505.2015.01.031. Deng Runfei, Guo Xiucheng. Modeling and characteristic analysis of spatial passenger linkage based on field theory[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2015, 45(1): 178-183. DOI:10.3969/j.issn.1001-0505.2015.01.031.(in Chinese)

[14]窦慧丽, 刘好德, 杨晓光. 基于站点上下客人数的公交客流OD反推方法研究[J]. 交通与计算机, 2007, 25(2): 79-82. DOI:10.3963/j.issn.1674-4861.2007.02.020. Dou Huili, Liu Haode, Yang Xiaoguang. OD matrix estimation method of public transportation flow based on passenger boarding and alighting[J].ComputerandCommunications, 2007, 25(2): 79-82. DOI:10.3963/j.issn.1674-4861.2007.02.020.(in Chinese)

[15]Li K, Gao Z, Ning B. Cellular automaton model for railway traffic[J].JournalofComputationalPhysics, 2005, 209(1): 179-192. DOI:10.1016/j.jcp.2005.03.016.

Network congestion evolution law of urban rail transit based on network passenger flow mode

Li Man Wang Yanhui Jin Jun Jia Limin

(1State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China)(2School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

To describe the passenger load state and the congestion evolution law, the concept and physical characteristics of the network passenger flow mode are presented based on the concept of the passenger flow gradient, including the free mode, the congestion mode and the congestion dissipation mode. The calculation formula of the passenger flow field strength is used to estimate the alighting ratio. The passenger load index of the platform and the passenger load index of the segment are chosen as the key parameters of the point congestion, and the values of the network passenger flow mode are calculated. The key parameters of passenger flow exchange under the condition of network operation are proposed,and the dynamic evolution model of the passenger flow based on cellular automata is established to study the dynamic propagation and evolution law of the network passenger flow and describe the evolution mechanism of the group behavior of the network passenger flow. Taking part of Beijing subway network as an example, based on the actual survey data of the passenger flow, the network mode value at different times are simulated by MATLAB through adjusting the boarding ratio. The results show that different modes of the network passenger flow are presented at different time and therefore the physical characteristics are verified.

urban rail transit; passenger flow mode; passenger flow field strength; congestion evolution; cellular automata model

10.3969/j.issn.1001-0505.2017.02.033

2016-07-31. 作者简介: 李曼(1986—)，女，博士生；贾利民(联系人)，男，博士，教授，博士生导师，jialm@vip.sina.com．

“十三五”国家重点研发计划资助项目(2016YFB1200402).

李曼,王艳辉,晋君,等.基于路网客流模态的城市轨道交通网络拥堵演变机理[J].东南大学学报(自然科学版),2017,47(2):404-409.

10.3969/j.issn.1001-0505.2017.02.033.

X913.4

A

1001-0505(2017)02-0404-06