基于动态子模型法的结构动响应预示方法

于士甲 张 鹏 李彦斌 吴邵庆 费庆国

(1东南大学土木工程学院, 南京210096)(2东南大学机械工程学院, 南京 211189)

基于动态子模型法的结构动响应预示方法

于士甲1张 鹏1李彦斌2吴邵庆1费庆国2

(1东南大学土木工程学院, 南京210096)(2东南大学机械工程学院, 南京 211189)

研究了基于动态子模型法的结构动响应预示方法基本理论,并建立了可应用于复杂切割边界条件下的匹配插值方法．首先以壳-壳及壳-体2种子模型为研究对象,探究动态子模型法在2种模型中的动响应分析精度及计算效率．以复杂卫星模型为研究对象,验证了动态子模型法在复杂结构中的应用性．研究结果表明:在保证局部运算精度的情况下,子模型法可以极大幅提高运算效率;壳-壳子模型法和壳-体子模型法通过1层切割边界节点和3层切割边界节点即可保证较高响应预示精度;在复杂结构中整体模型网格与子模型网格大小相差较大的情况下,子模型法仍能获得较理想的响应预示结果．

子模型法;局部响应;运算效率;切割边界;复杂结构

在建立复杂结构有限元模型时,受计算机硬件条件的限制,需合理设置有限单元的尺寸;同时为提高分析效率,通常对结构的一些局部细节采取一定的简化措施[1]．然而,设置较大单元尺寸及忽略结构细节会降低有限元分析结果的精度;对复杂结构进行总体建模分析时,或因单元尺寸过大难以获得精确的结果,或因总体模型过大无法求解[2]．对于大型薄壁结构,总体建模时大多采用壳单元模拟,但壳单元无法反应层间应力;对于大量螺栓连接结构,整体建模时由于忽略螺栓的局部细节,因而无法反映螺栓及其周边部位的局部响应;在单元连续性差的部位,引入MPC连接单元后,分析结果中出现应力集中的现象,故与实际情况不符．

针对上述问题,现阶段处理复杂结构响应预示问题主要采用以下2种方法:① 局部网格细化法,对结构的关键区域采用较小的单元模拟,其余部分采用较大的单元模拟[3];② 子结构法,将结构划分为若干子结构,在模态空间内通过缩减自由度来完成求解[4]．在局部网格细化法中,为保证单元连续性,模型中网格尺寸过渡区域难以保证单元质量;在具体关注区域未明确的情况下,需大量试算[3]．子结构法预示的结构响应精度与选取的自由度缩聚方案有关,所引起的分析误差难以评估[4]．

近年来,随着商用有限元软件的普及,子模型法在复杂结构局部响应预示中得到越来越广泛的应用．该方法从总体结构中切割出结构关键区域作为子模型,对子模型进行精细化建模,并将总体模型在切割边界上的位移响应作为强迫位移激励施加于子模型的切割边界,对子模型上得到的响应进行分析．根据圣维南原理,子模型在切割边界附近的响应预示结果可能存在较大误差,但在远离边界的区域,响应预示结果具有足够的精度．与局部网格细化法及子结构法相比,子模型法不需要设置网格尺寸过渡区域,减轻了建模工作量,在便于获取关键区域精确响应分布的同时提高了工作效率．

目前,子模型法借助Ansys内置的Sub-modelling模块,广泛应用于结构的尺寸优化[5-6]、机械构件的响应预示及强度评估[2, 7-9]、大型桥梁及地下工程的设计[1, 10-11]等众多工程领域．吴诰珪等[5]提出了静态力作用下子模型法的基本理论;Ramsay等[12]研究了不同单元类型对子模型法的响应预示精度的影响．目前,基于Ansys的子模型法要求子模型与整体模型空间位置一致,切割边界只能经过壳单元或体单元,这限制了子模型法的应用范围及进一步的发展．此外,目前尚未形成成熟的动态子模型法理论,其分析精度亦有待验证．

本文基于传统子模型法,推导得到基于动态子模型法的响应预示方法．并以对边简支板为研究对象,探究壳-壳及壳-体2种子模型法的准确性及高效性;进而以复杂卫星模型为研究对象,验证动态子模型法在复杂结构中的应用性．

1 基于动态子模型法的响应预示理论

考虑黏性阻尼时,结构振动的动力学方程可表示为

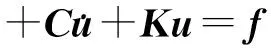
(1)

式中,M为结构质量矩阵;C为结构黏性阻尼矩阵;K为结构刚度矩阵;f为结构外荷载向量;u为结构待求位移向量．假设系统为线性系统,对式(1)在零初始条件下进行傅里叶变换,可得

DU=F

(2)

式中,D=K+jCω-ω2M为系统动刚度矩阵;U,F分别为u,f的傅里叶变换．

将结构分割为区域Ω1和区域Ω2两部分,如图1所示．其中,已知Ω1中位移响应,记切割边界上的节点位移为Ua,除Ua之外的节点位移为U1．Ω2中除边界上的节点位移外,其余节点的位移响应均为未知,记为U2．边界上节点位移Ua可通过下式求得:

(3)

式中,Fm,Dmn(m,n=1,a,2)分别为系统的分块载荷向量和动刚度矩阵．

图1 有限元分析模型

(4)

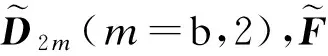
(5)

记切割边界为L,由整体模型在L上的节点位移向量Ua要插值获得子模型在L上的节点位移向量Ub，还存在以下2个关键问题:① 子模型与整体模型空间位置不对应问题;② 子模型与整体模型在切割边界上网格节点不重合问题．

为解决问题1,需要确定2个有限元模型之间的空间位置转换关系,即

Ub=UaQ+ΔU

(6)

式中,Q为3×3的坐标转换矩阵,

(7)

ΔU为平移向量:

(8)

为解决问题2,需对切割边界上的节点位移进行插值处理,位移Ua,Ub应满足下面的映射关系[13]:

Ub=GUa

(9)

式中,G为位移关联矩阵．

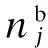
(10)

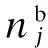
(11)

3个面积之和为

A=Ai1+Ai2+Ai3

(12)

(13)

由此,利用式(10)及(13)中节点位移的线性插值方法,即可获得子模型边界的节点位移．

2 动态子模型法响应预示分析流程

本文建立的结构动态子模型法具体流程如图2所示,虚线框所包含部分为自主编程实现过程．其技术路线如下:

1) 创建结构整体有限元模型,借助商用有限元软件MSC. Nastran进行动力学响应分析,得到结构整体位移响应．

2) 切割边界尽量避开应力集中位置,同时参考整体结构网格和几何特征,对所关心的区域建立精细化有限元子模型．

3) 提取整体结构切割边界的节点信息及位移响应,利用式(6)匹配模型空间位置关系,以及式(10)及(13)将位移插值到子模型边界对应节点．

4) 对精细化子模型在给定位移边界条件下进行分析,求解结构局部响应．

图2 子模型法计算流程图

与传统Ansys子模型法相比,上述基于动态子模型法的响应预示方法具有如下优势:总体模型与子模型的空间位置不必严格对应;总体模型与子模型在切割边界上的节点不必一一对应;切割边界没有单元类型的限制．

3 算例验证

3.1 研究对象

以对边简支板为研究对象,结构几何尺寸与材料参数如表1所示．本文建立了3个有限元模型,分别为粗糙整体模型(单元边长20 mm)、基于粗糙整体模型求解的精细化子模型(单元边长6.7 mm)及作为参照的精细化整体模型(单元边长6.7 mm)．假设板在长度方向0.4～0.6 m范围内为重点分析区域,设定为子模型,在整体模型上表面部分区域受P=1 Pa的均布压力,如图3所示．分析整体模型与子模型1～1 000 Hz的结构频率响应．

表1 板的几何尺寸及材料属性

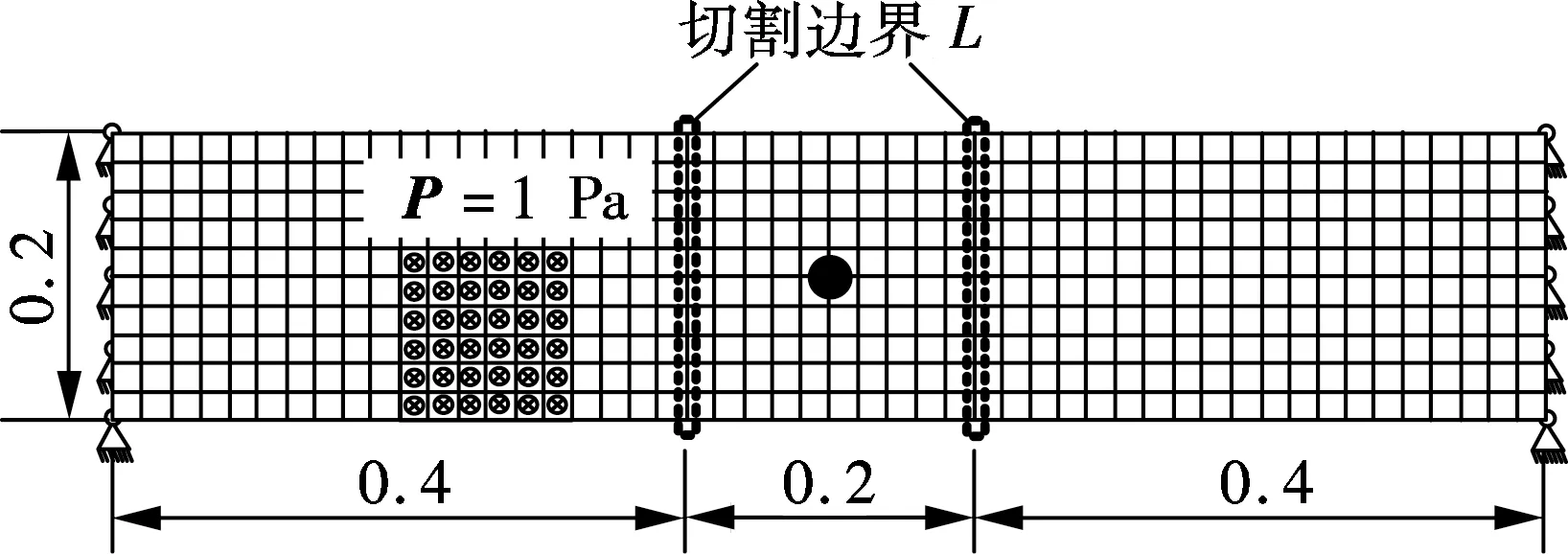
(a) 粗糙整体模型(单位：m)

(b) 子模型

(c) 精细化整体模型

3.2 壳-壳子模型法

大型复杂薄壁结构整体建模通常简化为壳单元,而子模型则可以根据具体情况选取合适的单元类型．如切割出来的子模型仍属于薄壁结构,则可以继续采用壳单元建模,称为壳-壳子模型法．

为验证壳-壳子模型法在响应预示中的准确性及计算效率,选取远离切割边界的模型几何中心作为响应关注位置,整体模型与子模型响应关注位置的位移与应力频率响应如图4所示,整体模型响应与子模型在500 Hz处的位移与Von Mises应力响应云图如图5所示．表2给出了子模型与精细化整体模型的计算时间．

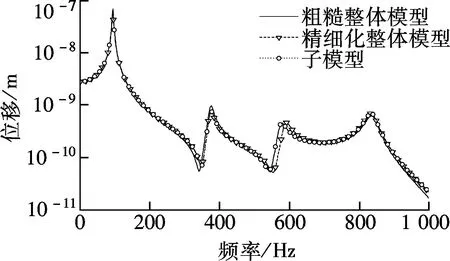
(a) 位移

(b) Von Mises应力

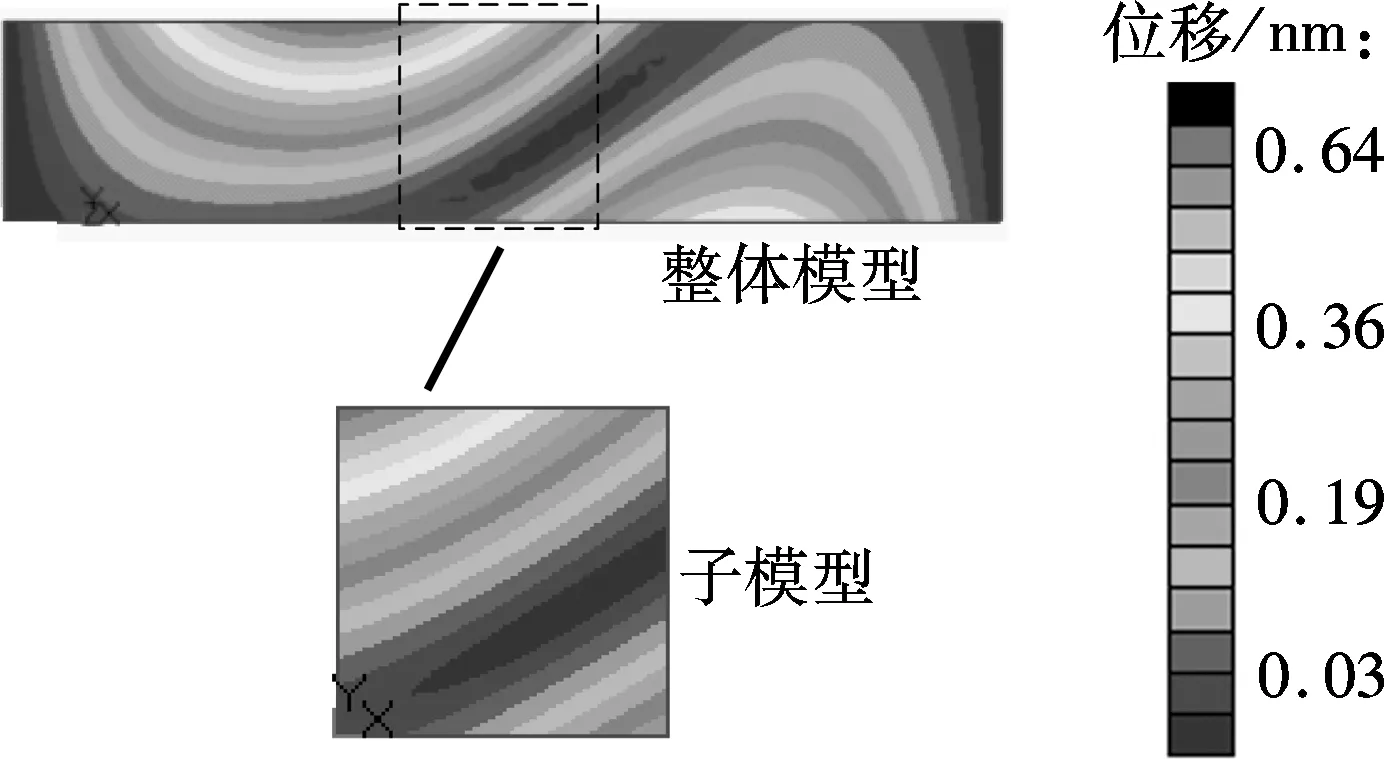
(a) 位移

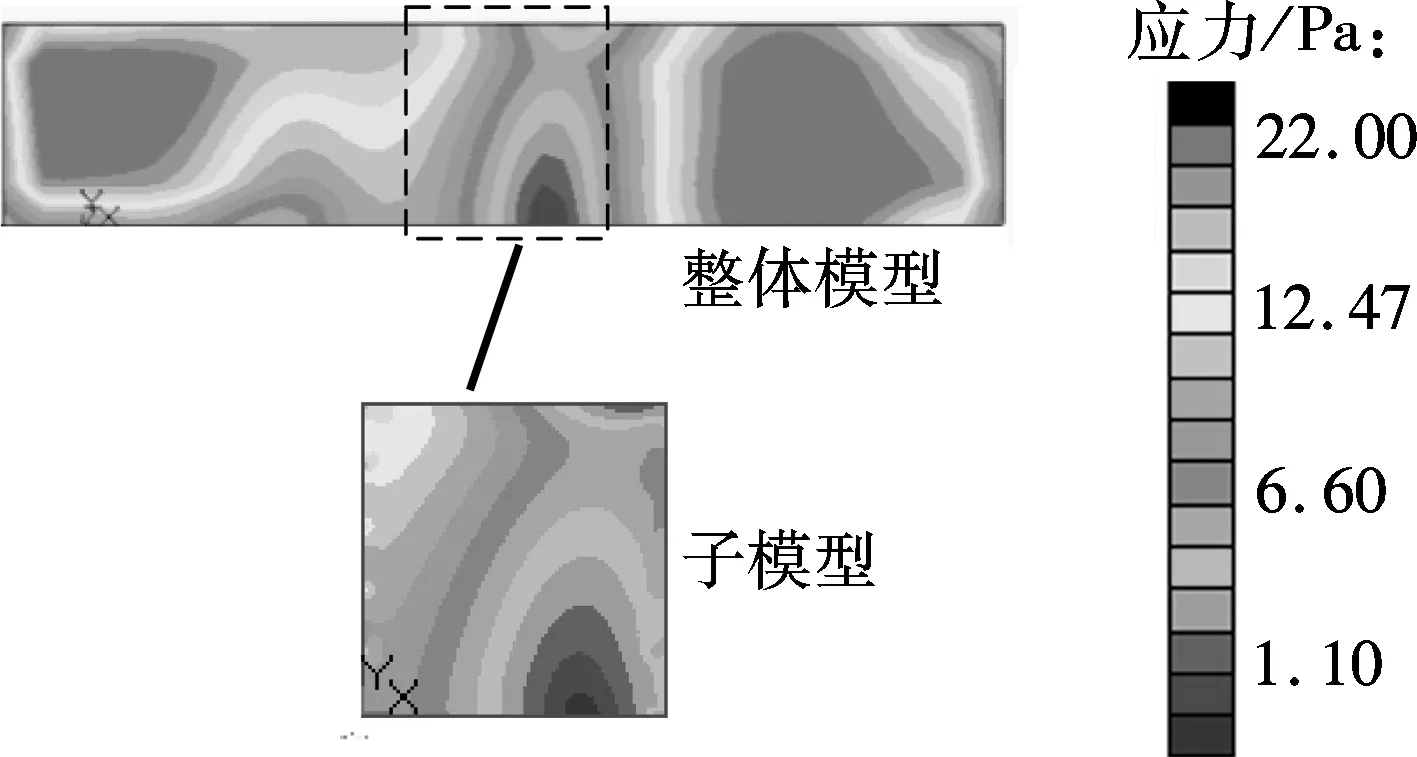
(b) Von Mises应力

表2 壳-壳子模型法计算时间对比

由图4分析可知:壳-壳子模型法具有较高精度,是一种有效的计算结构局部响应的手段,能够考虑更多局部信息,提高了整体模型的计算精度．由图5分析可知,子模型法位移连续性较好,这是由于子模型法基于位移求解,边界节点的线性插值方案能够较好模拟原模型边界节点的位移分布;在切割边界处,子模型法的应力与整体模型相差较大,在离切割边界较远处二者几乎相同,与圣维南原理所阐述的现象相同．由表2可知,与精细化整体模型求解方法相比,子模型法仅需其30%的计算时间,在保证精度的同时提高了计算效率．

3.3 壳-体子模型法

如果子模型不属于薄壁结构或需要考虑螺栓连接、层间应力等细节,则子模型必须采用实体单元建模,称为壳-体子模型法．与壳单元不同,普通实体单元上的节点只有3个平动方向自由度,无法模拟壳单元附带的3个转动方向自由度.为模拟转动位移,在切割边界上选取2层或3层单元节点作为切割边界进行插值．本文建立4个有限元模型,分别为粗糙整体模型(单元边长0.02 m)、子模型1(1层切割边界)、子模型2(2层切割边界)及子模型3(3层切割边界),其中3种子模型单元边长均为0.01 m．选取模型上表面中点作为响应关注位置,关注位置的位移与Von Mises应力频率响应如图6所示,子模型500 Hz的Von Mises应力响应云图如图7所示．表3给出了子模型与精细化整体模型的计算时间．

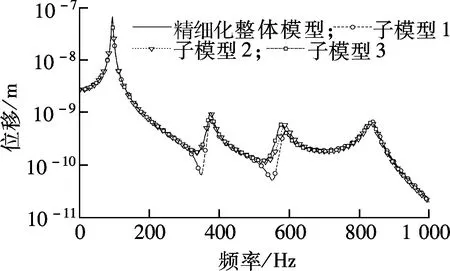
(a) 位移

(b) Von Misee应力

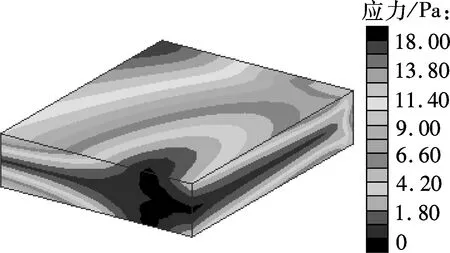
(a) 精细化整体模型

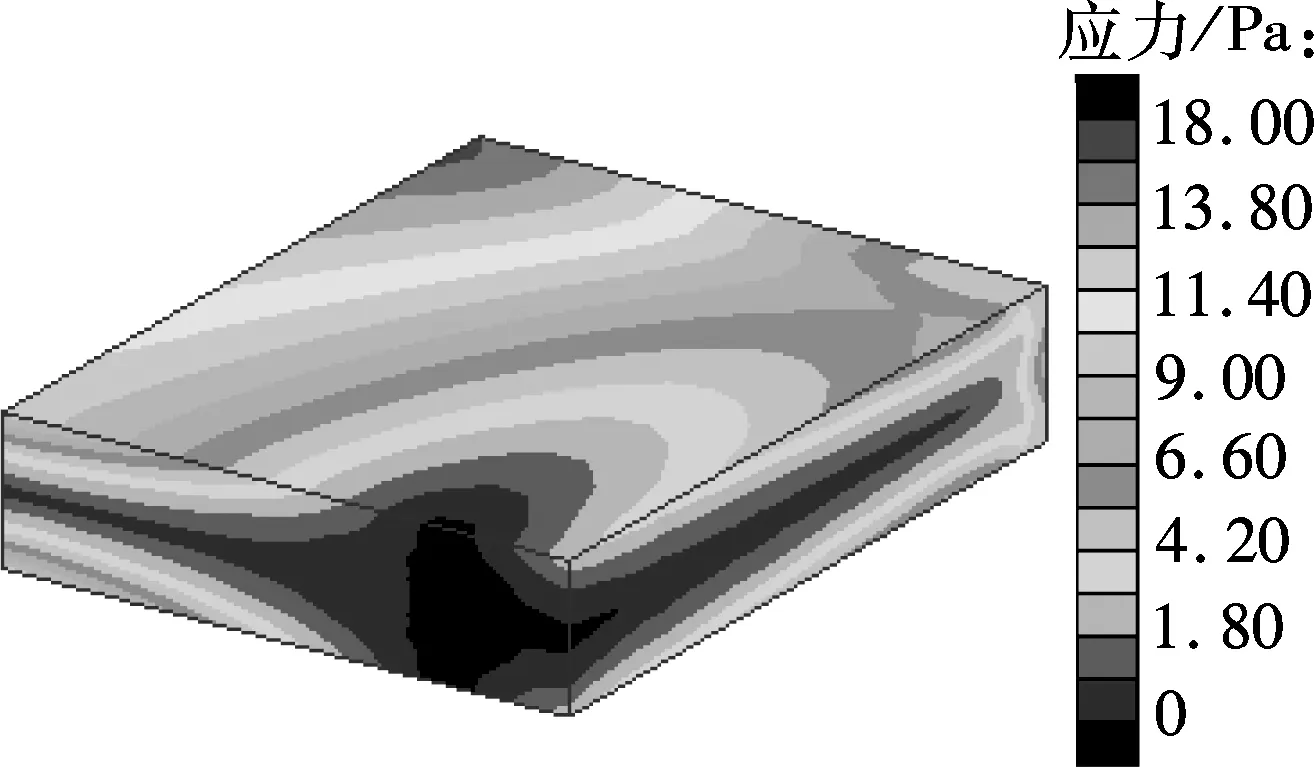
(b) 子模型3

由图6分析可知:壳-体子模型法具有较高精度;对位移来说, 1层切割边界的子模型结果不够准确,2层或3层切割边界的子模型结果与精细化整体模型吻合较好;对应力来说,1层或2层切割边界的子模型结果均不够准确,3层切割边界的子模型结果与精细化整体模型结构较吻合．由图7可以看出,在离切割边界较远处,能够体现出层间应力等壳单元无法获得的信息．由表3可知,与精细化整体模型求解方法相比,壳-体子模型法仅需其14.2%的计算时间,提高计算效率的效果十分明显．

表3 壳-体子模型法计算时间对比

4 复杂系统中的应用

以某型号卫星模型为研究对象,忽略卫星隔板间的连接,建立整体分析的粗糙有限元模型,切割边界单元大小为80 mm,如图8(a)所示．考虑隔板间螺栓连接,建立重点分析区域的子模型,切割边界单元大小为6 mm,其中图8(b)红心所示的某螺栓部位为分析的关注位置．结构在底部固支约束,卫星侧面受单位噪声压力．分析子模型在1～500 Hz内响应,关注位置的位移及Von Mises应力频响曲线如图9所示．

(a) 粗糙整体模型

(b) 局部精细化子模型

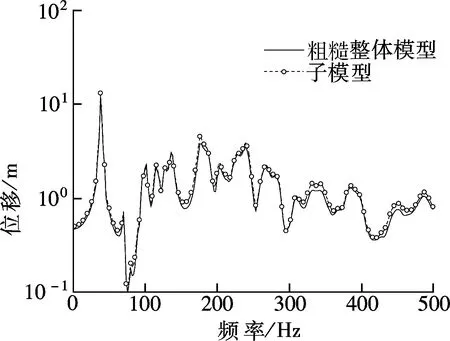
(a) 位移

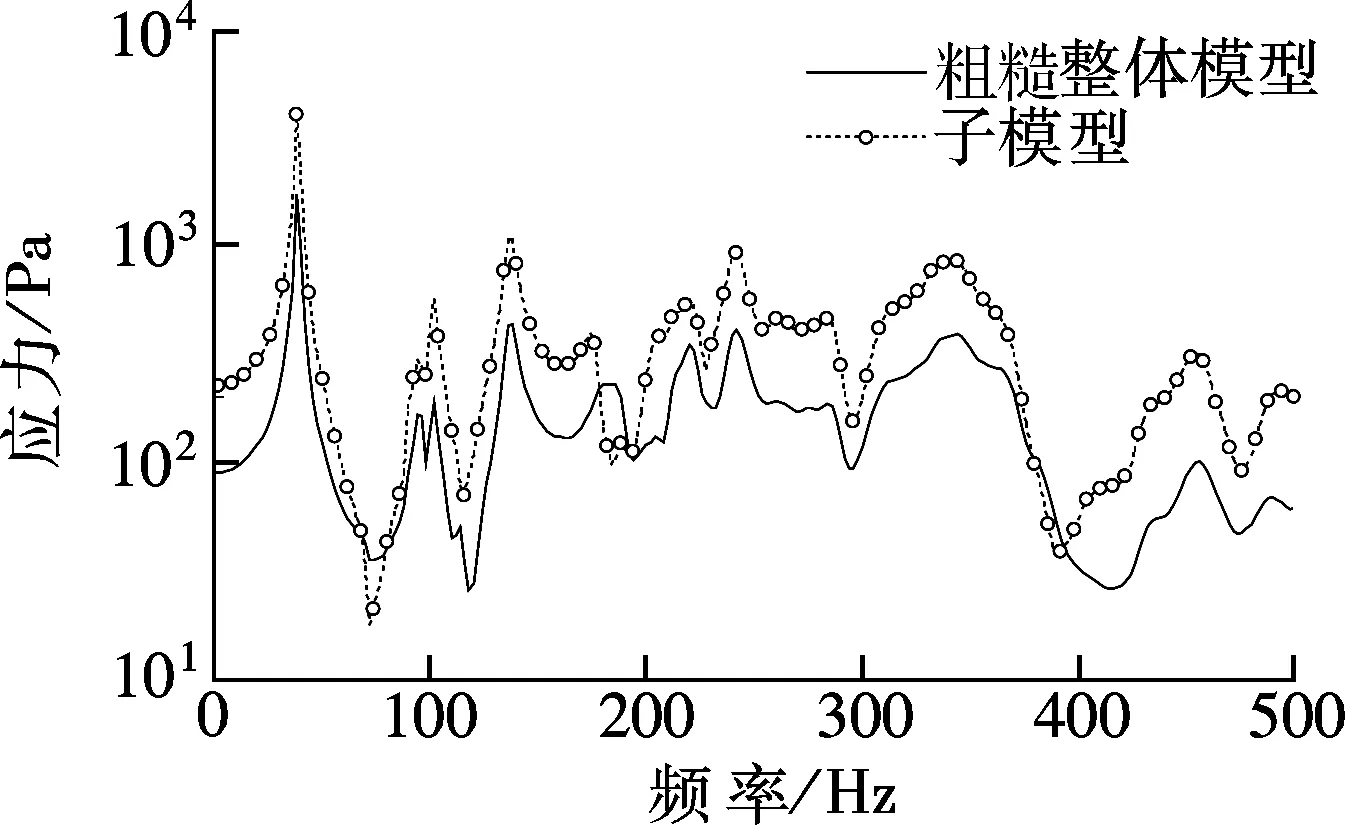
(b) Von Mises应力

由图9可知,即使粗糙整体模型与子模型结构细节不同、切割边界的单元尺寸相差巨大,结构位移响应仍基本吻合,说明结构位移响应预示精度对结构细节依赖程度不高;粗糙整体模型与子模型计算所得的应力响应相差较大,这表明粗糙的整体模型所计算的结果已不具有可信度,根据精细化子模型所求得的响应预示结果更能反映结构的真实受力情况．

5 结论

1) 壳-壳子模型法分析结果比原粗糙整体模型的分析结果更加精确;子模型位移与粗糙整体模型基本相同,子模型Von Mises应力在切割边界附近与粗糙整体模型有很大差异,远离切割边界的位置二者基本相同.

2) 壳-体子模型法中,欲保证子模型位移响应的准确性,切割边界应有2层插值节点;欲保证子模型应力响应的准确性,切割边界应有3层插值节点.

3) 壳-体子模型法中,子模型可较好体现层间应力等壳单元无法获得的信息.

4) 壳-壳子模型法与壳-体子模型法均可大幅提高计算效率.

5) 子模型法可应用于复杂结构中整体模型网格与子模型网格大小相差比较大的情况,且能得到较理想结果．

References)

[1]Aygül M, Al-Emrani M, Urushadze S. Modelling and fatigue life assessment of orthotropic bridge deck details using FEM[J].InternationalJournalofFatigue, 2012, 40(7):129-142. DOI:10.1016/j.ijfatigue.2011.12.015.

[2]Dai F, Xia K, Zheng H, et al. Determination of dynamic rock mode-Ⅰ fracture parameters using cracked chevron notched semi-circular bend specimen[J].EngineeringFractureMechanics, 2011, 78(15):2633-2644. DOI:10.1016/j.engfracmech.2011.06.022.

[3]Sun L, Zhao G, Ma X. Adaptive generation and local refinement methods of three-dimensional hexahedral element mesh[J].FiniteElementsinAnalysis&Design, 2012, 50(1):184-200. DOI:10.1016/j.finel.2011.09.009.

[4]王文亮, 杜作润. 动态子结构法的国内进展[J]. 力学进展, 1985, 15(1):23-32. Wang Wenliang, Du Zuorun. Advances of dynamic substructural method[J].AdvancesinMechanics, 1985, 15(1):23-32. (in Chinese)

[5]吴诰珪, 王继承, 许季. 子模型法在客车车身结构改进中的应用[J]. 华南理工大学学报(自然科学版), 2003, 31(2): 52-55. DOI:10.3321/j.issn:1000-565X.2003.02.012. Wu Gaogui, Wang Jicheng, Xu Ji. Application of sub-modeling in improving the bus-body structure[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2003, 31(2):52-55. DOI:10.3321/j.issn:1000-565X.2003.02.012. (in Chinese)

[6]史战新. 基于 Ansys 子模型法的肘板结构优化[J]. 舰船科学技术, 2014, 36(8): 19-26. DOI:10.3404/j.issn.1672-7649.2014.08.004. Shi Zhanxin. The bracket structure optimization based on Ansys sub-model method[J].ShipScienceandTechnology, 2014,36(8): 19-26. DOI:10.3404/j.issn.1672-7649.2014.08.004. (in Chinese)

[7]Zarzalejos J M, Fernndez E, Caixas J, et al. Bolted ribs analysis for the ITER vacuum vessel using finite element submodelling techniques[J].FusionEngineeringandDesign, 2014, 89(7): 1790-1794. DOI:10.1016/j.fusengdes.2014.04.025.

[8]Mandal N K, Dhanasekar M. Sub-modelling for the ratchetting failure of insulated rail joints[J].InternationalJournalofMechanicalSciences, 2013, 75(75):110-122. DOI:10.1016/j.ijmecsci.2013.06.003.

[9]Citarella R, Cricrì G. Three-dimensional BEM and FEM submodelling in a cracked FML full scale aeronautic panel[J].AppliedCompositeMaterials, 2014, 21(3):557-577. DOI:10.1007/s10443-014-9384-5.

[10]Hussein M, Hunt H, Kuo K, et al. The use of sub-modelling technique to calculate vibration in buildings from underground railways[J].ProceedingsoftheInstitutionofMechanicalEngineersPartFJournalofRail&RapidTransit, 2013, 229(3):303-314. DOI:10.1177/0954409713511449.

[11]赵大亮, 李爱群, 丁幼亮, 等. 基于子模型法的大跨斜拉桥扁平钢箱梁应力分析[J]. 计算力学学报, 2008, 25(3): 326-332. Zhao Daliang, Li Aiqun, Ding Youliang, et al. Stress analysis on steel-box girder of long span cable-stayed bridge based on submodel method[J].ChineseJournalofComputationalMechanics, 2008, 25(3):326-332. (in Chinese)

[12]Ramsay A C A, Maunder E A W. Sub-modelling and boundary conditions with p-type hybrid-equilibrium plate-membrane elements[J].FiniteElementsinAnalysis&Design, 2006, 43(2): 155-167. DOI:10.1016/j.finel.2006.08.002.

[13]齐朝晖, 孔宪超, 李坦. 复杂系统子结构界面缝合方法[J]. 工程力学, 2013, 30(9):10-15. Qi Zhaohui, Kong Xianchao, Li Tan. Substructure technique in the analysis of large-scale structure based on interfaces seaming[J].EngineeringMechanics, 2013, 30(9):10-15. (in Chinese)

Structural response prediction based on dynamic sub-modelling method

Yu Shijia1Zhang Peng1Li Yanbin2Wu Shaoqing1Fei Qingguo2

(1School of Civil Engineering, Southeast University, Nanjing 210096, China)(2School of Mechanical Engineering, Southeast University, Nanjing 211189, China)

Based on the theoretical derivation, the basic formula of the dynamic response of sub-modelling method was obtained based on structural dynamic stiffness under complex cutti4ng boundary conditions. Firstly, a sub-modelling method was studied by using 2 sub-models of shell-shell and shell-solid as a research object based on a simply supported plate. The accuracy and the high efficiency in the 2 sub-models were researched. Then, the good applicability of dynamic sub-modelling method on the complex structure was proved by using a satellite model as a research object. The results show that the computational efficiency is improved with the sub-modelling method under a premise of local computation precision. The high precision can be achieved with only 1 layer and 3 layers of boundary nodes when using shell-shell and shell-body sub-modelling methods, respectively. Fine results can also be obtained under the condition of a sharp incompatibility between the whole model and the sub-model on complex structures.

sub-modelling method; local response; computational efficiency; cutting boundary; complex structure.

10.3969/j.issn.1001-0505.2017.02.021

2016-09-04. 作者简介: 于士甲(1992—),男,硕士生;费庆国(联系人),男,博士,教授,博士生导师,qgfei@seu.edu.cn.

国家自然科学基金资助项目(11402052, 11572086)、教育部新世纪优秀人才支持计划资助项目(NCET-11-0086)、江苏省自然科学基金资助项目(BK20140616)．

于士甲，张鹏，李彦斌，等.基于动态子模型法的结构动响应预示方法[J].东南大学学报(自然科学版),2017,47(2):325-330.

10.3969/j.issn.1001-0505.2017.02.021.

V414.8;O32

A

1001-0505(2017)02-0325-06