页岩储层有机碳含量测井定量评价方法对比研究——以X地区研究为例

樊晓伊，姚光庆，赵乾辰，程 巍，李平和

(1.中国地质大学构造与油气资源教育部重点实验室，湖北武汉 430074；2.中国地质大学资源学院；3.中国石化河南油田物探技术研究院；4.中国石油辽河油田勘探开发研究院)

页岩储层有机碳含量测井定量评价方法对比研究
——以X地区研究为例

樊晓伊1,2，姚光庆1,2，赵乾辰3，程 巍4，李平和3

(1.中国地质大学构造与油气资源教育部重点实验室，湖北武汉 430074；2.中国地质大学资源学院；3.中国石化河南油田物探技术研究院；4.中国石油辽河油田勘探开发研究院)

有机碳含量是评价页岩气储层资源量的重要参数之一，利用测井资料计算有机碳含量，克服了样本分析测试的离散性和有限性等。通过对测井资料筛选校正，优选出响应特征明显的测井曲线；综合岩心测试分析数据，建立了改进△lgR法、多元回归分析法、BP神经网络法三种定量计算有机碳含量的模型，分析了模型的优缺点与适用性。X地区研究表明，三种有机碳含量评价模型均能在一定程度上满足该地区有机碳含量评价的需要，其中，BP神经网络法计算精度最高，适用性较强；在缺乏分析测试数据条件下，则应选用改进△lgR法。

页岩气储层；有机碳含量；测井模型；改进△lgR法；回归分析法；BP神经网络法

有机碳含量(TOC)是评价页岩储层生烃能力和资源量的重要参数之一。确定有机碳含量最常用的方法是地球化学测试分析方法[1-2]，受取心样品数量、分布和测试成本的限制，该方法仅能获得离散且有限的有机碳含量值，难以满足区域评价的需求[1-3]。测井资料具有纵向连续分辨率高、分布广泛的特点，受到国内外学者的关注和大量研究[1-10]。Passey等[11]提出用电阻率-孔隙度曲线叠合图法(即△lgR法)确定有机碳含量，该方法简单便捷，是应用较广的一种方法；国内学者朱光有等[12]、胡慧婷等[3]、李延钧[13]等对△lgR法进行了改进，提高了模型的适用性；为了解决输入与输出参数之间复杂的非线性问题，Huang等[14]、Mohammad等[15]、郭龙等[16]、熊镭等[2]将人工神经网络方法引入到有机碳含量预测中，该方法是目前精度较高的预测模型。本文通过改进△lgR法、回归分析法及BP神经网络法对该地区有机碳含量进行预测，建立定量解释模型，为X地区页岩油气资源评价及甜点区分布提供依据。

1 X地区有机碳含量评价模型

X地区页岩气储层处于深湖-半深湖-盐湖沉积环境，岩性以灰黑色-深灰色页岩为主，夹灰质页岩、白云质页岩、泥质粉砂岩、泥质白云岩，有机碳含量较高，页岩油气资源丰富，但有机碳含量评价缺乏有效的理论指导。

1.1 改进△lgR法

Passey等[11]提出的基于孔隙度曲线和电阻率曲线的△lgR法是目前应用较广、较成熟的一种方法。该方法是把算术坐标下孔隙度曲线(通常是声波时差曲线)叠加在对数刻度的电阻率曲线(最好是深电阻率曲线)上[1-2]。

ΔlgR=lg(R/R基线)+K(Δt-Δt基线)

TOC=ΔlgR×102.297-0.1688LOM+ ΔTOC

式中：ΔlgR——经过一定刻度的孔隙度曲线与电阻率曲线的幅度差；R——地层电阻率，Ω·m；R基线——非源岩的电阻率基线，Ω·m；Δt——声波测井读数，μs·m-1；Δt基线——非源岩的声波测井基线，μs·m-1；K——刻度系数，取决于孔隙度测井的单位；TOC——总有机质含量，%；LOM——热成熟度；ΔTOC——有机碳含量背景值，%。

从式中可以看出，为了获取有机碳含量值，需确定基线值、叠合系数、热成熟度与有机碳含量背景值。然而，每口井通常存在多个基线值，需分段求取有机碳含量，且每段内基线值也有变化，选取合适的基线值较困难。叠合系数的选取与烃源岩测井响应特征有关，随着叠合系数变化，ΔlgR与实测TOC的相关度会出现峰值[3，17]，此时的叠合系数为最优值，但其很难确定，求取的有机碳含量精度受限。成熟度参数主要由样品分析、埋藏史和热史评价中获得，受测试资料及实验分析技术限制，很难获取精准的成熟度参数。有机碳含量背景值主要由地质学者依据区域地质、地化资料估算获得，受主观经验影响大，若研究层段内发育多段贫有机碳泥岩，测井曲线叠合后，很难满足所有贫有机碳泥岩段ΔlgR为零或接近零。在有机碳含量较低时，模型计算的有机碳含量值偏大，需动态叠合测井曲线，较繁琐[17]。

针对上述问题，国内学者朱光有等[12]最早对公式进行推导简化；胡慧婷等[3]、李延钧等[13]也对公式进行详细推导论证。简化后公式如下：

TOC=a×lgR+b×Δt+c

(1)

式中，a，b，c——模型系数，通过研究区样品分析由最小二乘法拟合得到。

通过SPSS软件，对研究区有机碳含量进行拟合，建立模型如下：

TOC=0.449×lgR+0.020Δt-3.613

(2)

1.2 回归分析法

1.2.1 单测井参数回归分析

由于有机质密度小于黏土矿物，随着有机质和烃类气体含量增加以及微裂缝的存在，页岩气储层烃源岩地层密度值变得更低[1-2]。根据这一响应特征，Schmoker[4]和Hester[5]利用密度测井曲线建立了地层有机碳含量定量评价模型；Lin等[18]研究指出，密度的倒数与有机碳含量有较高的相关性。

在有机质、二氧化硫、硫化氢等还原物质的作用下，铀离子被还原为二氧化铀沉淀下来，页岩储集层段的黏土矿物含量较高，伽马测井为高值，伽马能谱曲线往往表现为高铀、低钾、低钍的特征，且随着铀含量、铀钍比增大，有机碳含量逐渐升高[19]。Schmoker[6]、陆巧焕等[19]及Meyer等[20]学者分别用铀含量、铀钍比和伽马测井值来预测地层有机碳含量。

在页岩气储集层中，黄铁矿相对富集，降低了电阻率测井曲线值，使密度测井值增大[1-2]。Witkowsky[8]基于黄铁矿与岩心有机碳含量的相关性建立了回归方程，预测地层有机碳含量。

1.2.2 多元回归分析法

受烃源岩沉积环境、地层岩性、烃类饱和度等的影响，单测井曲线往往很难精确表达有机碳含量变化特征，为此，国内外学者[1，9-10，21]综合考虑多测井参数响应特征，用多元回归分析技术来建立测井解释模型，提高了模型的精度和适用性。

Mendelson和Toksoz[9]通过交会图法筛选出与有机碳含量关系密切的测井曲线，首次利用多元回归分析建立了有机碳含量与伽马、密度、声波时差、中子等测井曲线的关系，提高了有机碳含量计算的精度；国内学者[3，10，21]建立了不同地区自然伽马、自然伽马能谱、密度、中子孔隙度、声波时差、电阻率等多种测井参数与有机碳含量的多元回归模型，进一步扩大了模型应用范围。

本地区自然伽马、自然伽马能谱铀含量、密度等测井曲线与岩心有机碳含量相关性较差，单测井模型精度很低，难以达到区域评价需求。通过敏感性分析(图1)，筛选出相关性较好的补偿中子、声波时差、密度测井曲线建立多元回归模型，相关系数为0.773。

TOC=(0.109×φN-0.013Δt+

63.314)/ρ-21.422

(3)

式中：ρ——岩石的密度，g·m-3。

1.3 BP神经网络法

BP 神经网络算法是在误差反向传播理论基础上提出的反向传播学习算法，利用最速梯度下降法，使权值沿着误差函数的负梯度方向改变，通过反复的正向、反向学习，使误差信号达到最小。该方法具有很强的非线性动态处理能力，很好地表达了各输入与输出参数的隐式非线性对应关系[2，14，22-23]。

为消除测井响应深度与岩心分析数据深度不同给预测成果造成的影响，首先对岩心进行归位，避免数据运算中数量级差别造成网络预测误差，对样本参数进行归一化处理，并通过试算法确定隐含层节点数为5。选取与其有一定相关关系的自然伽马能谱铀含量、补偿中子、声波时差、密度等测井曲线作为BP神经网络的输入参数(图1)，通过对35个样本反复训练，使预测值不断逼近样本值，从而选择最优预测模型。从图2可以看出，BP神经网络训练模型与岩心有机碳含量相关度较高，能很好地预测有机碳含量。

2 应用效果分析

根据以上分析结果，分别对改进△lgR法、多元回归分析法、BP神经网络法进行数据处理与预测。从图3和图4可看出：①预测效果从差到好依次为改进△lgR法、多元回归分析法、BP神经网络法。多元回归分析法综合考虑了多测井参数的优点，比改进△lgR法具有更高的预测精度；BP神经网络解决了测井参数与有机碳含量之间很难用显示方程表达的复杂非线性关系，通过对样本反复训练，不断逼近期望值，使模型精度不断提高；②三种方法预测结果相对误差大部分在30%以下，一定程度上满足了有机碳含量评价的需要；③在岩性较纯、厚度较大的泥页岩层段，模型预测值与样本值吻合程度高；在岩性复杂的灰质泥岩、白云质泥岩、砂质泥岩层段误差较大。

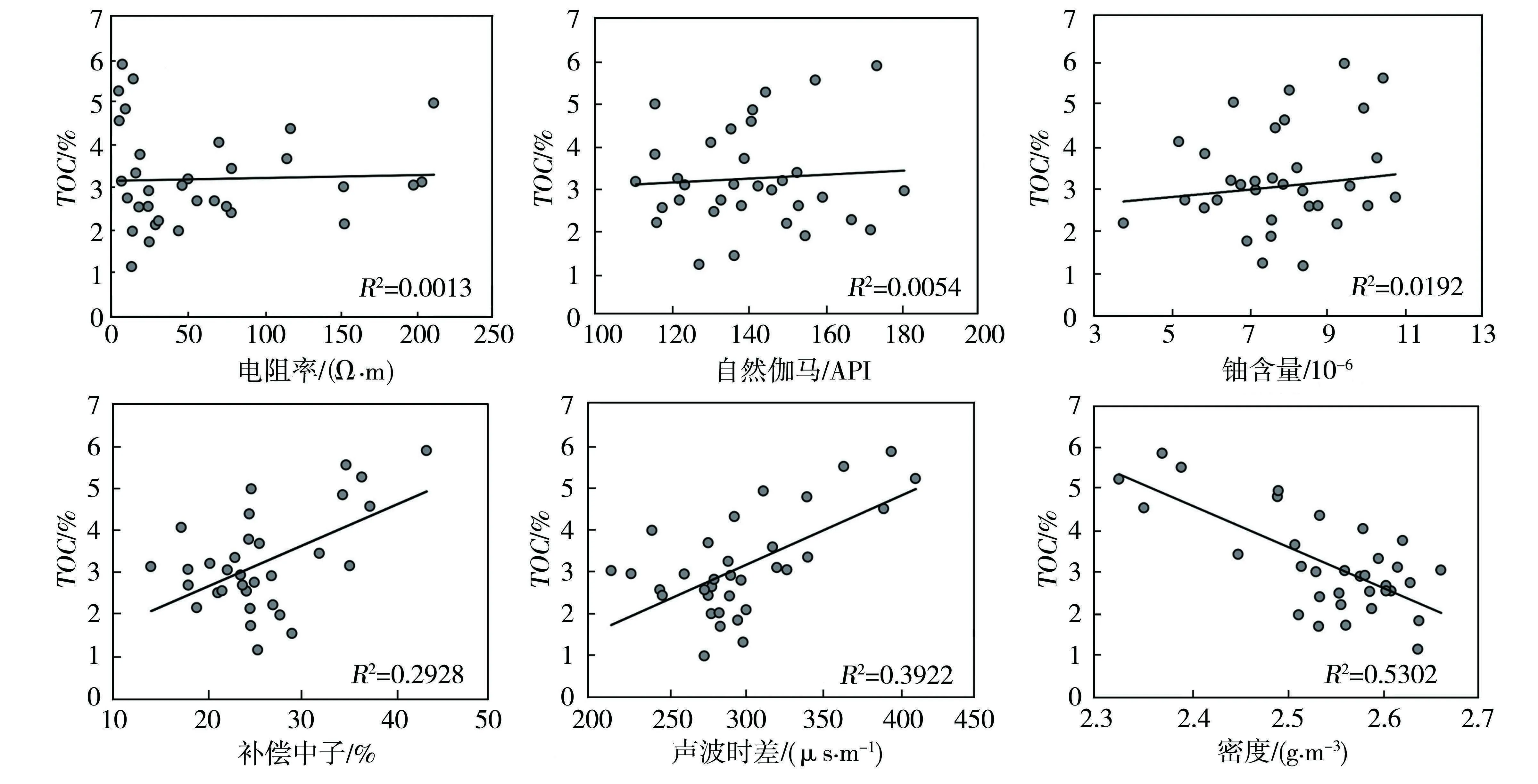
图1 岩心有机碳含量与各测井值交会图

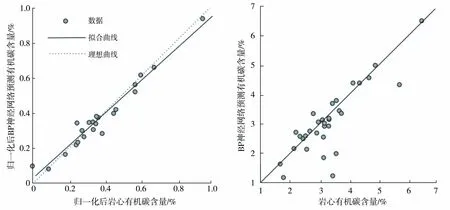
图2 岩心有机碳含量与BP神经网络预测有机碳含量交会图

3 模型误差与适用性分析

改进△lgR法只需声波时差和电阻率参数，不要求成熟度参数，无须人为确定基线值、有机碳含量背景值[2-3]，大大提高了模型的便捷性，且受样品测试分析数量的影响较小。在缺乏测试数据的条件下，该方法具有很大优势。

X地区页岩目的层岩性较复杂，黏土矿物中伊/蒙混层以及黄铁矿较发育，两者均可降低电阻率响应特征[2]，弱化有机碳含量变化造成的差异，使改进的△lgR法存在一定的误差。该方法忽略了自然伽马、密度、中子等对有机碳响应密切的测井曲线信息，具有一定的局限性[2-3]。

在使用多元回归分析方法计算有机碳含量过程中，筛选出的测井曲线与岩心有机碳含量虽具有一定的响应关系，但受地层岩性、黄铁矿、烃类流体等的影响，测井曲线往往是这些因素交叉综合响应的结果，不能完全反映地层有机碳含量的变化[2]。多元回归分析方法强化了有机碳测井响应特征，但并不能消除其它因素的影响，从而造成一定的偏差；且拟合成果需要充分的测试分析数据，具有很大的局限性。

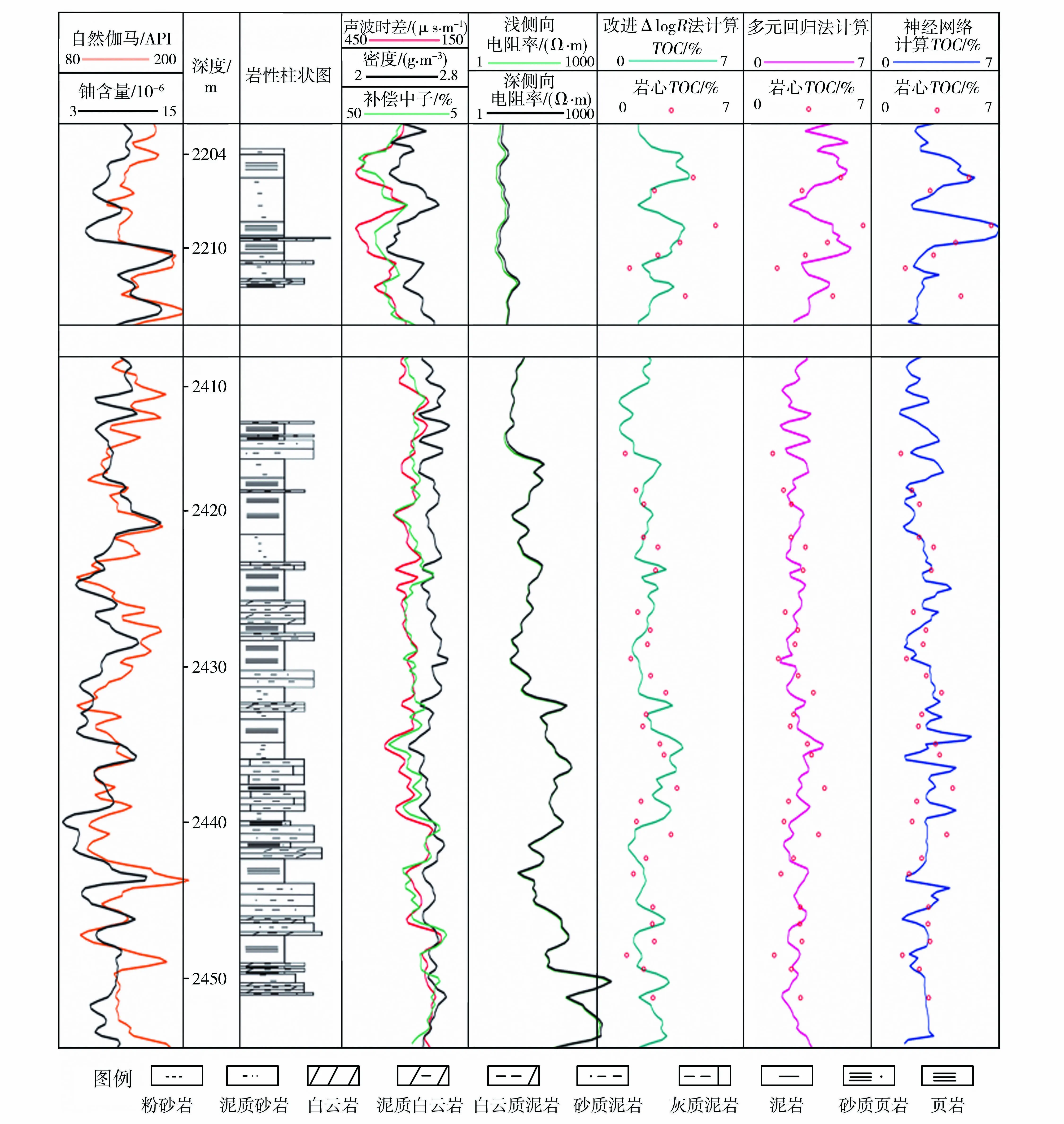
图3 模型计算有机碳含量与岩心有机碳含量对比

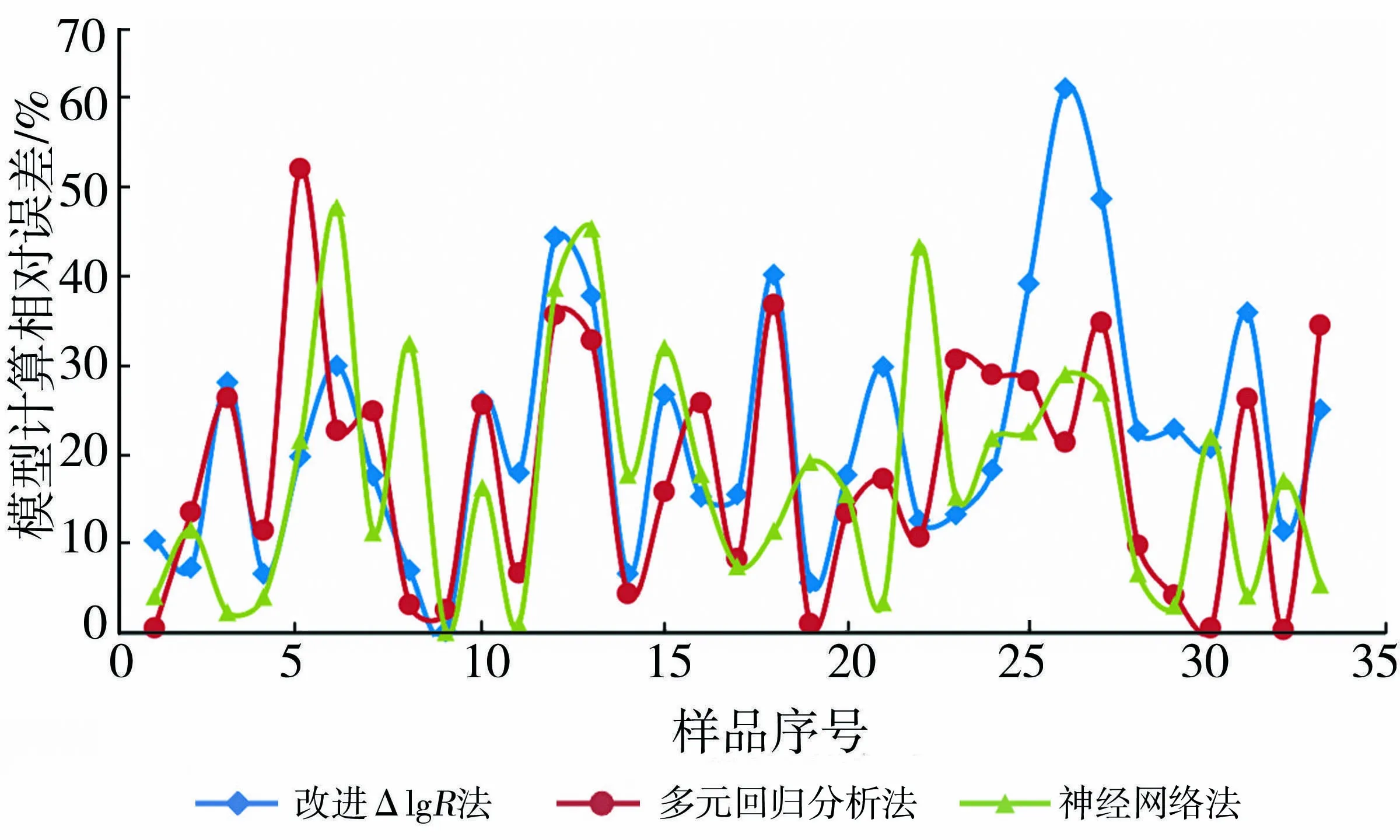
图4 岩心有机碳含量与模型计算值相对误差

BP神经网络结构的确定主要依据经验确定，标准BP算法在误差下降时，难免产生振荡现象，严重影响网络的收敛速度，且容易陷入局部极小值，很可能误认为找到最佳权重而停止学习，影响模型精度，从而存在误差[2，23]。网络训练精度同样受样本大小的影响，具有一定的局限性。该方法很好地解决了测井参数与有机碳含量的复杂非线性问题，在计算精度方面具有很大的优势，是适用性较强的一种方法。

4 结论

(1)传统的△lgR法需要确定基线值、叠合系数、成熟度参数及有机碳含量背景值，合理的参数设置需要依据经验与充分的实验分析资料，难度较大；改进的△lgR法避免了这一弊端，只需孔隙度与电阻率测井曲线，应用方便。

(2)受目的层岩性、黄铁矿、烃类流体等的影响，单测井曲线不能完全反映地层有机碳含量的变化，通过相关性分析，筛选出响应特征明显的测井系列，建立了多元回归模型，计算精度得到提高。

(3)BP神经网络法很好地解决了测井信息和有机碳之间的隐式非线性问题，并综合多测井参数信息，经过大量反复训练，预测精度最高，具有广阔的应用前景。

(4)改进△lgR法、多元回归分析法、BP神经网络法均有一定优缺点与适用性，在具体评价过程中，应根据不同区域情况，选择合适的计算方法。在缺乏测试数据时，可选用改进△lgR法；在测试数据较充足时，BP神经网络法计算精确度最高。

[1] 徐思煌, 朱义清. 烃源岩有机碳含量的测井响应特征与定量预测模型[J].石油实验地质, 2010, 32(3): 290-295.

[2] 熊镭,张超模,张冲,等.A地区页岩气储层总有机碳含量测井评价方法研究[J].岩性油气藏, 2014, 26(3): 74-78.

[3] 胡慧婷,卢双舫,刘超,等. 测井资料计算源岩有机碳含量模型对比及分析[J].沉积学报, 2011, 26(6): 1199-1205.

[4] SEHMOKER J W. Determination of organic content of Appalachian Devonian shales from formation-density logs[J].AAPG Bulletin, 1979, 65(7):1285-1298.

[5] SEHMOKER J W，HESTER T C. Organic carbon in Bakken Formation, United States Portion of Williston Basin[J].AAPG Bulletin, 1983, 67(12), 2165-2174.

[6] SEHMOKER J W.Determination of organic-matter content of Appalachian Devonian shales from gamma-ray logs[J].AAPG Bulletin, 1981, 65(7)：2165-2174.

[7] FERTLE H. Total organic carbon content determined from well logs[J].SPE Formation Evaluation, 1988, 3(2): 407-419.

[8] WITKORSRY J, GALFORD J, QUIREIN J. Predicting pyrite and total organic carbon from well logs for enhancing shale reservoir interpretion[R].SPE 161097,2012.

[9] MENDELSON J D, TOKSOZ M N. Source Rock Characterization using multivariate analysis of log data[A].SPWLA twenty-sixth Annual Logging Symposium, 1985.

[10] 汤永梅,梁兴,周松源,等.利用测井资料评价白驹凹陷烃源岩[J].西部探矿工程, 2010, 22(1): 137-139.

[11] PASSEY Q R, CREANEY S, KULLY J B. A Practical model for organic richness from porosity and resistivity logs[J].AAPG Bulletin, 1990, 74(5): 1777-1794.

[12] 朱光有,金强,张林哗.用测井信息获取烃源岩的地球化学参数研究[J].测井技术, 2003, 27(2): 104-104.

[13] 李延钧,张烈辉,冯媛媛,等.页岩有机碳含量测井评价方法及其应用[J].天然气地球科学, 2013, 24(1): 169-175.

[14] HUANG Z H, WILLIAMSON M A. Artificial neural network modeling as an aid to souck rock characterization[J].Marine and petroleum geology, 1996, 13(2): 277-290.

[15] MOHAMMAD R K, AHAD A M. Total organic carbon content determined from well logs using △lgRand Neuro Fuzzy techniques[J].Journal of Science and Engineering, 2004, 45(3-4): 141-148.

[16] 郭龙,陈践发,苗忠英.一种新的TOC含量拟合方法研究与应用[J].天然气地球科学, 2009, 20(6): 951-956.

[17] 刘超. 测井资料评价烃源岩方法改进及作用[D].黑龙江大庆：东北石油大学, 2011.

[18] LIN J L, SALISCH H A. Determination from well logs of the total organic carbon content in potential source rocks[J].SPE 27627,1993.

[19] 陆巧焕,张晋言,李绍霞.利用测井资料进行生油岩评价[J].勘探地球物理进展, 2006, 29(2): 140-144.

[20] MEYER B L, NEDERLOF M H. Identification of source rocks on wireline logs by density/resistivity and sonic transit time/resistivity cross plots[J].AAPG Bulletin, 1984, 68(11): 121-129.

[21] 赵彦超.生油岩测井评价的理论和实践[J].地球科学，1990, 15(l): 65-74.

[22] 朱振宇,王贵文,朱广宇.人工神经网络法在烃源岩测井评价中的应用[J].地球物理学进展, 2002, 17(1): 137-140.

[23] 杨建,杨程博,张岩,等.基于改进神经网络的渗透率预测方法[J].岩性油气藏, 201l, 23(1): 98-102.

编辑：王金旗

1673-8217(2017)02-0048-05

2016-11-22

樊晓伊，1987年生， 2009年毕业于西南石油大学石油工程专业，现为中国地质大学(武汉)2013级在读博士研究生，主要从事储层地质学方面研究。

P631.8

A