基于地理加权回归模型的思茅松生物量遥感估测
闾妍宇,李 超,欧光龙,熊河先,魏安超,张 博,胥 辉
(西南林业大学西南地区生物多样性保育国家林业局重点实验室,昆明650224)
基于地理加权回归模型的思茅松生物量遥感估测
闾妍宇,李 超,欧光龙,熊河先,魏安超,张 博,胥 辉
(西南林业大学西南地区生物多样性保育国家林业局重点实验室,昆明650224)
通过调查云南省景谷县思茅松林120株单木数据,构建思茅松单木生物量模型。结合2005年景谷县TM影像数据及2006年森林资源二类调查小班数据,采用普通最小二乘模型 (OLS)和地理加权回归模型 (GWR)的方法构建思茅松生物量遥感估测模型。结果表明:地理加权回归模型比普通最小二乘模型具有更好的拟合效果,其决定系数 (R2)显著高于OLS模型,Akaike信息指数 (AIC)相比降低7.832;两种模型通过独立样本检验可以看出,模型预估精度从OLS模型的72.70%提高至GWR模型的75.06%;通过GWR模型反演计算,研究区内思茅松林单位面积生物量为49.02t/hm2,比实测数据低1.229%,与实测数据基本吻合,且估算误差优于OLS模型;基于GWR模型估算的景谷县思茅松林总生物量为2.101×107t。可见基于地理加权回归方法估测森林地上生物量的方法是有效的,能提高森林生物量遥感估测模型的拟合和预估精度,可以用于思茅松林的生物量的遥感估算。
思茅松;生物量;遥感;普通最小二乘;地理加权回归
森林是最大的陆地生态系统,森林生物量是评价森林生态系统的碳循环的重要载体及指标参数[1]。传统的森林生物量调查方法有:样地清查法、生理生态模型法和遥感估算法[2]。随着技术手段的不断发展,现今广泛应用遥感(RS)、地理信息系统(GIS)和全球卫星定位系统(GPS)等3S技术结合的手段,调查区域森林生物量。国庆喜等[3]以小兴安岭南坡为研究对象,结合TM影像和森林资源一类清查样地数据,讨论环境因子、生物因子和遥感因子与生物量的相关关系,构建了森林生物量的回归方程,获得了较好的估测精度;曾晶等[4]利用高分一号遥感影像,建立生物量的多元线性模型,反演精度为80.75%;李明诗等[5]结合光谱、纹理以及地形特征等信息来研究森林生物量,发现纹理特征可以提高森林生物量的估测精度,并且不同树种与不同特征之间存在不同的相关性。孙雪莲等[6]应用随机森林方法结合遥感因子研究思茅松人工林生物量,估测出人工林单位面积生物量59.09t/hm2,总生物量为3.644×106t。
国内外对森林生物量进行了很多研究,但林木生长并非一个独立的过程,会与周围树木产生相互影响,即林木生长表现出一定的空间效应。在进行森林调查中获取的数据都与地理位置有关,地理位置间的邻近关系使得观测数据具有空间关系[7-8],经典统计学模型往往忽视这种空间关系,往往导致分析的结果是有偏的[9-10]。Fotheringham等在局域光滑理论的基础上提出了一种局域模型方法,他将空间信息考虑到回归参数中,在每一个点上都用权函数来回归参数,直观显示了空间的非平稳性,之后,利用这种方法提出了地理加权回归模型(Geographically Weighted Regression Model,GWR)[11-12],该模型现在经济学,气象学,生态学以及林学等学科得到广泛应用。刘畅等应用普通最小二乘模型,线性混合效应模型和地理加权回归模型分析了不同尺度下黑龙江省森林碳储量空间分布,结果表明,地理加权回归模型能够很好地解决空间效应问题并提高拟合精度[13]。戚玉娇通过遥感信息和实测数据相结合,构建地理加权回归模型来分析大兴安岭森林地上碳储量,结果表明,GWR模型解决了空间非平稳性、提高了估测精度[14]。郭含茹等[15]通过构建不同权函数的地理加权回归模型分析遥感因子与碳储量的相关性,表明GWR模型在区域碳储量估测上是合理且精度较高的。
基于此,本研究以云南省景谷傣族彝族自治县为研究区,利用实测样地数据,森林资源二类调查数据和TM影像数据建立回归模型,在考虑空间效应的基础上,估测思茅松森林生物量,对比普通最小二乘模型(Ordinary Least Square,OLS)与地理加权回归模型(GWR)的估测精度,选择最优的估测模型来反演景谷县思茅松林生物量,为丰富估测区域森林生物量/碳储量提供一定的研究案例与方法。
1 研究区概况
本研究区域位于云南省景谷傣族彝族自治县,总面积7 550km2。景谷位于横断山脉无量山西南端,澜沧江以东,地处东经100°02'~101°07',北纬22°49'~23°52'。地势以山地高原为主,谷坝镶嵌其中,山地、高原、盆地相间分布,总体地势由北向南倾斜,渐向东西两翼扩展,最高海拔2 920m,最低海拔600m;属亚热带山原季风气候,境内山高谷深,海拔差异大,气候呈明显的垂直变化。
全县地形以山区半山区为主,年平均气温22.1℃,年降水量1 354mm。景谷县拥有林业用地58.36万hm2,占总面积的77.5%,森林覆盖率达到74.7%,其主要树种为思茅松。思茅松不仅是当地主要用材树种,也是主要的造林树种。
2 数据收集与处理
2.1 基础数据
本研究的基础数据是2006年森林资源二类调查小班数据,2006年二类森林资源实测样地数据及补充调查的思茅松样地数据共计90块,如图1 (右)。依据随机抽样方法将样地分为模型构建样地71块与独立性检验样地19块,样地大小为30m× 30m;样地调查因子包括:坐标、龄组、株数、蓄积量、平均树高、平均胸径等。
样木数据是2012年的实测样木数据。在结合样地进行实地调查,考虑径阶分布的基础上,总计调查120株样木,记录各样木的基本信息,包含GPS坐标、海拔、坡度、坡向、胸径、树高等因子。

图1 景谷县遥感影像(左)和思茅松样地分布图(右)Fig.1 Remote sensing image and distribution of Simao Pine forest and the sample distribution in Jinggu County
2.2 遥感数据处理
本研究采用2005年行带号分别为130/44,131/43,131/44的3景TM5遥感影像数据,对3景影像分别在ENVI 5.1软件下进行辐射定标,大气校正,几何校正和地形校正,之后在此基础上进行裁剪、拼接,获得景谷县TM影像图,如图1(左)。
2.3 单木生物量模型构建
按照胥辉、张会儒的生物量测定和建模方法[16],幂函数在模型拟合过程中容易收敛,且模型拟合效果较好,故本研究思茅松单木生物量模型选择幂函数,选择变量胸径(D)、树高(H)或者组合变量(D2H)来进行模型构建。

表1 单木生物量模型拟合结果Tab.1 Estimation parameters of the individual tree biomass equations
本研究采用表1模型构建思茅松单木生物量模型并估算单木生物量,选择决定系数(R2)最高的模型,故模型2为单木生物量最优拟合模型。估算样地地上生物量采用单木生物量数据和平均标准木法计算样地林分单位面积生物量,见公式(1)。

式中:Wabv为样地思茅松地上总生物量;a,b,c为单木生物量模型估算参数;D为每个样地标准木平均胸径;H每个样地标准木平均树高;N为每个样地株数。
2.4 遥感特征信息提取
本研究利用ENVI 5.1软件提取景谷县TM影像6个单波段、植被指数(NDVI,RVI,DVI,Albedo,VIS123,SAVI等),纹理特征(窗口大小分别为5× 5,7×7,9×9,15×15)、主成分变换和K-T变换等共计219个波段信息。
2.5 变量筛选
将提取的219个遥感特征波段导入 ArcGIS 10.2软件,与样地点叠加,提取每个样地点对应的遥感特征值,最后分析样地生物量与各个遥感因子的相关性。利用SPSS软件进行生物量与遥感因子的相关性分析,共计36个有遥感因子与生物量相关性显著(p≤0.05),如表2。将36个显著遥感因子进行逐步筛选,变量选进的显著性水平设定为进入p≤0.05,剔除p≥0.1,在SPSS软件中,仅有ME7_7因子通过筛选。

表2 思茅松生物量与遥感因子相关性分析Tab.2 Correlation between Pinus kesiya biomass and the remote sensing factors
3 研究方法
3.1 普通最小二乘模型
普通最小二乘模型,其自变量与因变量的关系可以通过最小二乘方法来表示:

式中:β是利用数据估计出的模型系数,ε是模型残差,且服从N(0,σ2)分布。参数β采用因变量与预测值之间的离差平方和为最小的方法来估计,可以表示为矩阵形式:

3.2 地理加权回归模型
林业数据普遍存在空间非平稳性,回归参数在不同地理位置上都是变化的,如果采用传统全局回归模型,会导致生物量估算结果有偏[19]。地理加权回归模型是基于普通全局回归模型的扩展,将空间影响考虑到模型构建中,以距离权重的形式加入到模型之中,故地理加权回归模型的基本形式为[8]:

式中:(ui,vi)表示i点处坐标,y(ui,vi)表示i点处的因变量,n表示样本个数,xni表示第n个变量在i的值,β0表示截距,βn表示第n个变量的回归参数,εi表示误差项,通常假定其服从N(0,σ2)。
在此模型中,每个样地点的回归参数都是不同的,可使用空间距离权重函数的方法解决,其基本形式为[7]:
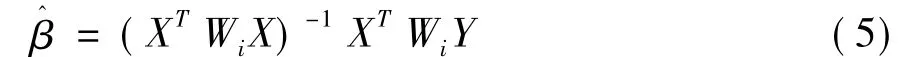
式中:Wi是点i处的空间权重对角线矩阵,Wi=diag(Wi0,Wi1,…,Win)。
由上式可以看出,解决GWR的参数估计问题,关键之处在于如何定义空间权重矩阵,也就是如何选择空间权重函数。一般选择广泛应用的Guass函数法,其基本形式为[13]:

式中:b是bandwidth,即带宽,是一个非负衰减参数用来表示权重与距离之间函数关系。
带宽的过小或者过大,都会影响拟合精度。故在模型拟合过程中要不断进行带宽的选择以确定最佳带宽,常用的带宽确定方法包括:交叉验证法(CV),Akaike准则(AIC)和贝叶斯信息准则(BIC)。本研究主要采用AIC方法来确定最佳带宽。
AIC信息准则是在对最大似然原理进行修正的基础上得到的。在一般情况下,假设模型的似然函数为L(θ,x),θ的维数为p,x为随机样本,故AIC的定义为[13]:

式中:θ^
L为θ的最大似然估计,q为未知参数的个数。在带宽判断中,AIC值最小处的带宽是最优模型带宽。
3.3 平稳性检验
GWR模型是一种解决空间效应的方法模型,将模型更好地应用于实际问题时,还需要进行平稳性统计检验。平稳性检验包括:回归关系的全局平稳性检验和各回归参数的平稳性检验[18]。
1)全局平稳性检验
检验GWR模型的拟合精度对比OLS模型有显著提高,即检验假设:

若H0为真时,则认为对所给定数据集GWR模型和OLS模型无显著差异,数据可用OLS模型进行拟合,从而回归关系关于空间位置的变化是全局平稳的。若H0为假,则拒绝该假设,GWR模型在拟合上显著优于OLS模型。
2)各回归参数的平稳性检验
该检验应用置信区间检验的方法,检验各回归参数平稳性。将GWR模型的局部参数与普通回归模型的全局固定参数作对比,若局部估计的参数四分位值波动大于全局估计参数的两倍标准误值,则认为模型的参数是显著非平稳的。若某个参数变化不显著,则应把该参数当作常数来处理和解释。
3.4 模型评价与独立性样本检验
本研究模型评价主要是通过计算模型的决定系数(R2)、均方根误差(RMSE)和AIC信息准则对构建的两种模型(OLS和GWR)进行评价。
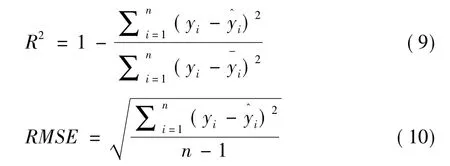
通过选取总体相对误差(RS)、平均相对误差(EE)、总体相对误差绝对值(RMA)和预估精度(P) 4个指标进行模型的独立性样本检验。

式中:yi为实测值;y^i为估计值;n为样本容量。
3.5 生物量反演
根据景谷县2006年小班调查数据,提取思茅松小班分布图,利用OLS和GWR模型确定的回归参数和自变量特征值进行估算景谷县思茅松林生物量数据。
4 结果分析
4.1 模型拟合
本研究借助SPSS软件和GWR 4.0软件分别对OLS和GWR模型进行拟合,选择训练样本(71块)对两种模型进行拟合。在最优自变量筛选时,采用逐步回归方法,对选取与样地生物量显著相关的36个遥感因子进行逐步回归和多重共线性分析,最后确定模型自变量为ME7_7。
在进行生物量建模时,将自变量与因变量进行对数变换,即假设模型为:

对数转换后的数据容易进行统计处理,且经对数转换后的数据能满足线性化的假设,可用线性模型理论估计生物量,使问题简化。将确定的遥感因子参与建模,分别构建OLS和GWR模型。
图2所示,GWR 4.0软件选择的GWR模型最佳带宽,AIC值最小的点,带宽最佳(b=15346.59m)

图2 GWR模型最佳带宽确定Fig.2 Selection of the optimal bandwidth for GWR model

表3 OLS和GWR模型拟合统计量Tab.3 Fitting statistics of both models by OLS and GWR
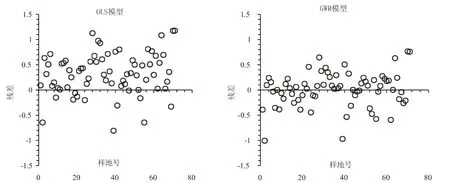
图3 两种模型残差分布图Fig.3 Distribution of the residuals
表3给出了2个模型4个评价指标,可以看出GWR模型的AIC值比OLS模型小7.832。根据经验,当GWR模型的AIC与OLS模型的AIC之差大于2时,则GWR模型相比于OLS模型更可靠,且GWR模型对比OLS模型的RMSE更小,R2更高,说明GWR模型的解释能力优于OLS模型。通过这些指标对比分析,GWR模型在模型拟合精度和预估上较OLS模型有一定程度改善。
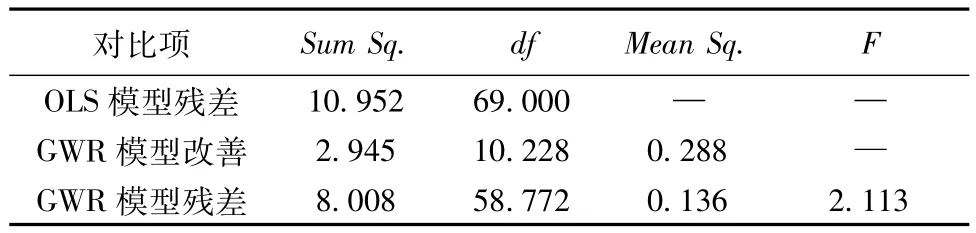
表4 GWR模型方差分析Tab.4 Variance analysis of GWR
通过表4方差分析结果可以看出,GWR模型的残差平方和由10.952降低到8.008,均方残差降低了0.288,F值为2.113,表明GWR和OLS模型拟合效果显著的不同。GWR模型要优于OLS模型。
分别绘制了OLS模型和GWR模型的残差分布图(图3),GWR模型的残差分布区间小于OLS模型的残差分布,且GWR模型残差绝对值大于1的只有一个点,OLS模型则有4个。说明GWR模型比OLS模型有更好的拟合效果。
4.2 平稳性分析
GWR模型参数波动的剧烈程度是判断模型参数在整个研究区内是否有显著变化的标准。若模型参数非平稳性显著,则表明该模型能更多地反应空间异质性。如表5和表6所示,根据置信区间检验方法,GWR模型截距上下四分位数值的差值(0.127)大于全局回归模型截距的标准误一倍范围,波段ME7_7上下四分位数值的差值(0.056)小于全局回归模型ME7_7回归参数标准误一倍范围。说明截距回归参数存在明显的空间非平稳性,ME7_7变量回归参数虽然存在一定的空间非平稳性,但并不显著,ME7_7的回归参数被考虑为常数项,β=-0.155。如图4所示,截距回归参数存在显著的空间非平稳性,故在进行局部回归估计时,与OLS的全局参数对比,有剧烈波动。

表5 OLS模型全局回归参数描述Tab.5 Descriptive statistics of the global regression parameters of OLS

表6 GWR模型回归参数描述Tab.6 Descriptive statistics of the local regression parameters of GWR
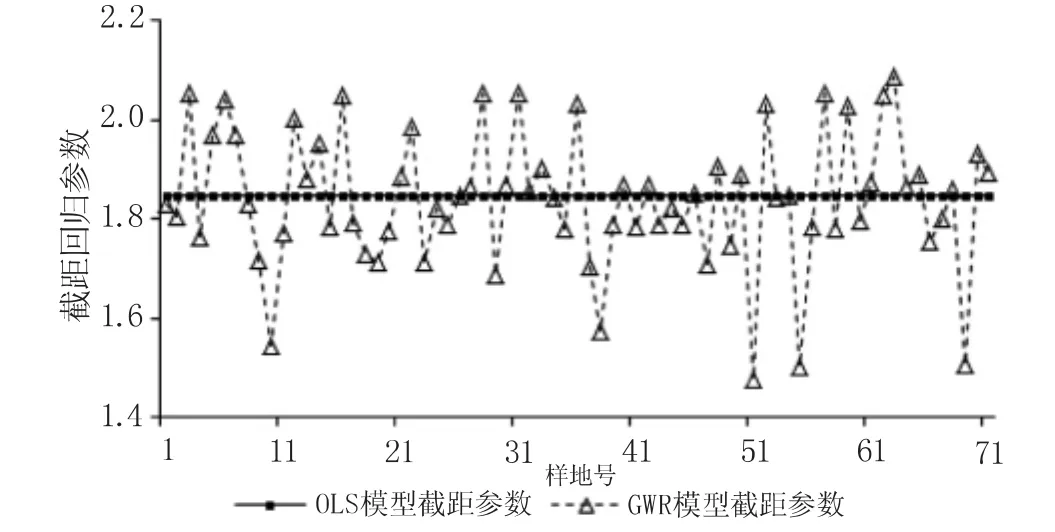
图4 两种模型截距回归参数曲线Fig.4 Regression parameter curve for GWR and OLS
4.3 独立性样本检验
从模型的拟合过程来看,地理加权回归模型在估测研究区内思茅松森林地上生物量空间分布上表现出较为明显的优势。本文应用随机抽样的19个样本对OLS和GWR模型进行独立性样本检验,进一步对比检验地理加权回归模型与最小二乘模型的预测能力。从表7检验结果对比显示:GWR模型在总相对误差、平均相对误差、总体相对误差绝对值3个指标上对比OLS模型都有一定的降低,其预估精度则提高2.36%。说明GWR模型在拟合效果上优于OLS模型,对森林生物量分布估测也更为精确。

表7 两种模型独立性检验Tab.7 The sample test of independence for the OLS and GWR models
4.4 景谷县思茅松生物量反演
如表8所示:OLS模型估测思茅松单位面积生物量为45.77t/hm2,地上总生物量为1.962×107t; GWR模型估测单位面积生物量为49.02t/hm2,思茅松地上总生物量为2.101×107t,两种模型思茅松地上生物量分布如图5所示。依据样地数据统计分析,景谷县单位面积思茅松生物量为49.63t/hm2,OLS模型估测的单位面积生物量低于实测数据7.778%;GWR模型估测的单位面积生物量低于实测数据1.229%,GWR单位面积生物量估测值与实测值基本吻合。

表8 两种模型反演结果Tab.8 Model reversion results for OLS and GWR models

图5 景谷县思茅松地上生物量分布图Fig.5 Distribution of Simao Pine forest biomass in Jinggu county
5 结论与讨论
通过拟合两种模型进行对比,GWR模型的决定系数(R2)大于OLS模型,且GWR模型的AIC值较OLS模型有了一定的改善;通过独立性样本检验的4个指标可以看出,GWR模型在生物量估测精度上优于OLS模型;GWR模型反演景谷县思茅松地上总生物量为 2.101×107t,单位面积生物量为49.02t/hm2,同实测单位面积生物量基本吻合。GWR模型在模型拟合和预估精度上与刘畅[13],戚玉娇[14],郭含茹等[15]通过GWR模型拟合林木地上生物量/碳密度时得到的结论是一致的。地理加权回归模型考虑了数据集的空间位置信息,为分析回归关系的空间特性创造了条件[8]。林业数据本身存在明显的空间效应,通过地理加权回归的方法拟合森林生物量,克服了空间异质性,拟合精度高于普通最小二乘模型。
本研究仅有一个遥感因子参与模型构建,主要因为:ME7_7因子与生物量的相关性达到-0.349,在0.01的显著水平下呈最大负相关。同时在逐步回归筛选中,也仅有ME7_7因子通过筛选。本研究在模型拟合过程中试图引入其他显著因子进行联合构建,但多个联合建模因子间存在多重共线性问题,使得GWR模型的拟合精度低于单因子建模精度,故在建模过程中只选取ME7_7。
地理加权回归模型在估测森林生物量时,带宽是影响估测精度的重要指标。本研究通过GWR 4.0软件选择Akaike信息准则和Gaussian函数法寻找最优带宽,在带宽表现形式上有最佳固定距离和最佳临近点,带宽选择方法上还有截尾bi-square函数法,在最佳带宽验证上还有交叉验证准则(CV)等,不同的方法选择的带宽大小也不尽相同,而带宽影响拟合精度。针对不同的研究区域,不同的研究数据选择合适的方法和验证指标确保GWR模型估测精度,将是进一步研究的方向。
[1]Brown S,Sathaye J,Cannell M,et al.Mitigation of carbon emissions to the atmosphere by forest management[C]//Proceedings of the IEICE General Conference.Japan:The Institute of Electronics,Information and Communication Engineers,1996:9735-9746.
[2]岳彩荣.香格里拉县森林生物量遥感估测研究[D].北京林业大学,2012.
[3]国庆喜,张锋.基于遥感信息估测森林的生物量[J].东北林业大学学报,2003,31(2):13-16.
[4]曾晶,张晓丽.高分一号遥感影像下崂山林场林分生物量反演估算研究[J].中南林业科技大学学报,2016(1):46-51.
[5]李明诗,谭莹,潘洁,等.结合光谱、纹理及地形特征的森林生物量建模研究[J].遥感信息,2006(6):6-9.
[6]孙雪莲,舒清态,欧光龙,等.基于随机森林回归模型的思茅松人工林生物量遥感估测[J].林业资源管理,2015(1):71-76.
[7]玄海燕,罗双华,王大斌.GWR模型中权函数的选取与窗宽参数的确定[J].甘肃联合大学学报:自然科学版,2008,22(3):10-12.
[8]玄海燕,黎锁平,刘树群.地理加权回归模型及其拟合[J].甘肃科学学报,2007,19(1):51-52.
[9]Zhang L,Shi H.Local modeling of tree growth by geographically weighted regression[J].Forest Science,2004,50(2):225-244.
[10]Zhang L,Ma Z,Guo L.Spatially assessing model errors of four regression techniques for three types of forest stands[J].Forestry: Oxford,2008,81(2):209-225.
[11]Fotheringham A S,Brunsdon C,Charlton M.Geographically Weighted Regression:the analysis of spatially varying relationships[J].American Journal of Agricultural Economics,2004,86(7): 554-556.
[12]Brunsdon C,Fotheringham A S,Charlton M.Geographically Weighted Regression:a method for exploring spatial nonstationarity[J].Stata Technical Bulletin,1996,28(4):281-298.
[13]刘畅.黑龙江省森林碳储量空间分布研究[D].哈尔滨:东北林业大学,2014.
[14]戚玉娇.大兴安岭森林地上碳储量遥感估算与分析[D].哈尔滨:东北林业大学,2014.
[15]郭含茹,张茂震,徐丽华,等.基于地理加权回归的区域森林碳储量估计[J].浙江农林大学学报,2015,32(4):497-508.
[16]胥辉,张会儒.林木生物量模型研究[M].云南科技出版社,2002.
[17]胥辉,岳彩荣,基于遥感技术的香格里拉县森林景观变化与森林生物量估测研究[M].云南科技出版社,2014.
[18]玄海燕,王静.地理加权回归模型的平稳性检验[J].甘肃联合大学学报:自然科学版,2006,20(5):10-12.
[19]张博,欧光龙,孙雪莲,等.空间效应及其回归模型在林业中的应用[J].西南林业大学学报,2016,36(3):144-152.
Remote Sensing Estimation of Biomass of Pinus kesiya var.langbianensis by Geographically Weighted Regression Models
LYanyu,LI Chao,OU Guanglong,XIONG Hexian,WEI Anchao,ZHANG Bo,XU Hui
(Key Laboratory of State Forestry Administration on Biodiversity Conservation in Southwest China,Southwest Forestry University,Kunming 650224,Yunnan China)
The Biomass model of Simao pine(Pinus kesiya var.langbianensis)was built based on the data collected from 120 Simao pine sampling trees,Landsat TM images in 2005 and the data of forest resource inventory in 2006 in Jinggu County,Yunnan Province.Then the remote sensing biomass estimation Model of Simao Pine were built by the ordinary least square(OLS)and geographically weighed regression(GWR) .The results showed that:GWR model had a better fitting effect than OLS,in which coefficient of determination(R2)was significantly bigger than the OLS model,Akaike information index(AIC)reduced by 7.832;It was obviously depicted from the sample test of independence that model prediction accuracy was improved from 72.70%(OLS)to 75.06%(GWR).The unit-area biomass was 49.02t/hm2by inversion,and basically consistent with the measured data;it was lower than the measured data 1.229%,and less than the estimation value of OLS.The total biomass of Simao pine in Jinggu County was 2.101×107t based on GWR model.The study indicated that forest aboveground biomass estimation based on geographically weighed regression(GWR)model could improve effectively the fitting accuracy of forest biomass estimation model,and could be used to estimate the biomass of Simao pine forest by remote sensing.
Pinus kesiya var.langbianensis,biomass,remote sensing,ordinary least square(OLS),Geographically Weighted Regression(GWR)
S718.55;S771.8
A
1002-6622(2017)01-0082-09
10.13466/j.cnki.lyzygl.2017.01.015
2016-11-15;
2016-12-09
国家林业公益性行业科研专项项目(201404309);国家自然科学基金项目(31560209);西南林业大学博士科研启动基金(111416)
闾妍宇(1991-),男,湖北监利人,在读硕士,主要研究方向:3S技术在林业中的应用。Email:395778724@qq.com
胥辉(1960-),男,博士,教授,主要从事森林计测学方面的研究。Email:zyxy213@126.com

