移动荷载作用下半无限弹性空间中地铁隧道动力响应的频域—波数域比例边界有限元法分析

雷晓燕，徐　斌,，徐满清

(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌　330013；2.南昌工程学院 土木与建筑工程学院，江西 南昌　330029)

半无限弹性空间内移动荷载动力响应问题有较广泛的工程背景，如地铁隧道列车引起的振动、地面车辆所引起的振动及其波的传播等。因此分析半无限弹性空间中移动载荷的动力响应，在岩土工程、交通工程等领域具有重要意义。

目前，对半无限线弹性空间的简单几何构形，如均质半无限空间的表面移动载荷问题，可利用解析方法进行计算[1-3]。对复杂几何构形，如地下任意形状空洞的移动载荷响应问题，主要是采用有限元法、边界元法及有限元—边界元耦合法等数值分析方法。相比于具有几何外形的结构，移动荷载作用下的半无限空间动力响应问题要复杂得多，一般只采用有限元法[4-6]，主要是由于要获得足够计算精度，需建立有效的人工边界及合理的离散网格，并且地基离散范围必须足够大。对于人工边界问题，国内外学者进行了广泛、深入的研究，建立了透射边界模型，如黏性及黏弹性边界[6-7]、叠加边界[8]、旁轴边界[9]、暂态透射边界[10-11]、多向及双渐近多向透射边界[12-13]等。各种边界模型的动力有限元法，在分析无限域地基土体动力问题时具有一定优势，但仍存在低阶边界精度不足、高阶边界稳定性差等问题，不具有有限元意义上的精确性，即离散网格无限小时数值解可以收敛到精确解；另一方面，由于其对离散区域和单元尺寸的要求，常使得计算模型具有极大的自由度，这样就导致计算时间较长，占用计算机资源较大，尤其对于三维动力有限元模型，其计算甚至难以实现。

在处理无限和半无限空间问题中，边界元法由于具有自动满足无穷远处辐射条件及降维的功能而被广泛应用[14-16]。该方法对移动载荷和周围介质相互作用的分析无疑具有重要意义，但形成边界元法的积分方程所需的基本解一般较复杂，特别是对于各向异性材料，甚至不存在基本解析解。另一方面，边界积分方程的奇异积分甚至是超奇异积分的处理，以及边界积分方程数值求解，难度相当大，限制了边界元法等的进一步应用。结合边界元法、有限元法各自所具有的优越性而形成的有限元—边界元耦合方法，已在结构—地基相互作用分析中得到了广泛应用[17-18]，但在处理结构与地基的接触面、层状土体的层间面等，有限元单元与边界元单元的耦合变形协调存在一定的困难。

比例边界有限元方法是以有限元法为基础的一种边界单元法[19]，它不需要求解基本解，因而能够有效地处理解析解特别复杂的满足一定条件的各向异性介质问题；同时，通过相似中心的合理选取，比例边界有限元法能够满足Sommerfeld的辐射条件。目前比例边界有限元法已应用于时域、频域中无限域波动问题分析、无限域地基的边界动力刚度矩阵求解等[20-21]。已有研究表明：比例边界有限元法对于处理大部分无限域、各向异性介质、材料不均匀变化等问题是非常精确、有效的[22]。

对于半无限空间中的移动荷载问题，考虑到荷载运动方向与结构的一致性，进行空间域—波数的积分变换，可极大减少计算量[6, 16-17]。值得指出的是，利用频域—波数域比例边界有限元法，得到半无限空间土体的精确动力刚度，分析时间—空间域土体动力响应问题，尚未有文献报道。基于此，本文拟利用荷载移动方向的空间到波数域的傅里叶积分变换，结合伽辽金法，建立频域—波数域的比例边界有限元方程，分析时间—空间域移动荷载作用下半无限弹性空间中地铁隧道的动力响应。

1　比例边界坐标系下频域—波数域内的控制方程

1.1　物理模型与比例边界坐标系

半无限弹性空间中移动荷载作用示意图如图1所示，移动荷载沿地铁隧道纵轴线z方向以速度v运动，且地铁隧道横截面保持不变。

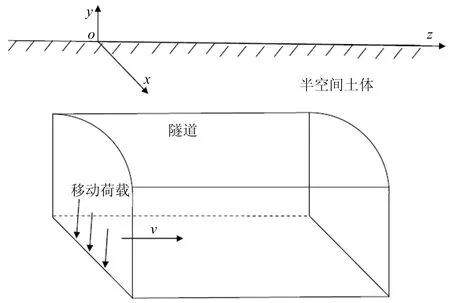
图1　半无限弹性空间中移动荷载作用示意图

沿地铁隧道轴线z向移动的分布线荷载，在地铁隧道底面y=-h(h为隧道埋深)有如下边界条件：

(1)

式中：σx，σy，σz分别为x，y，z方向的应力；Fn为荷载集度；δ为Dirac—δ函数；v为荷载移动速度；t为时间；a为移动荷载分布长度。

将边界条件进行t→ω和z→kz的傅里叶变换，则频率—波数域中边界条件为

-a≤x≤a

(2)

式中：kz为傅里叶变换域的波数；ω为频率；上标-和～分别表示频域、波数域内的量。

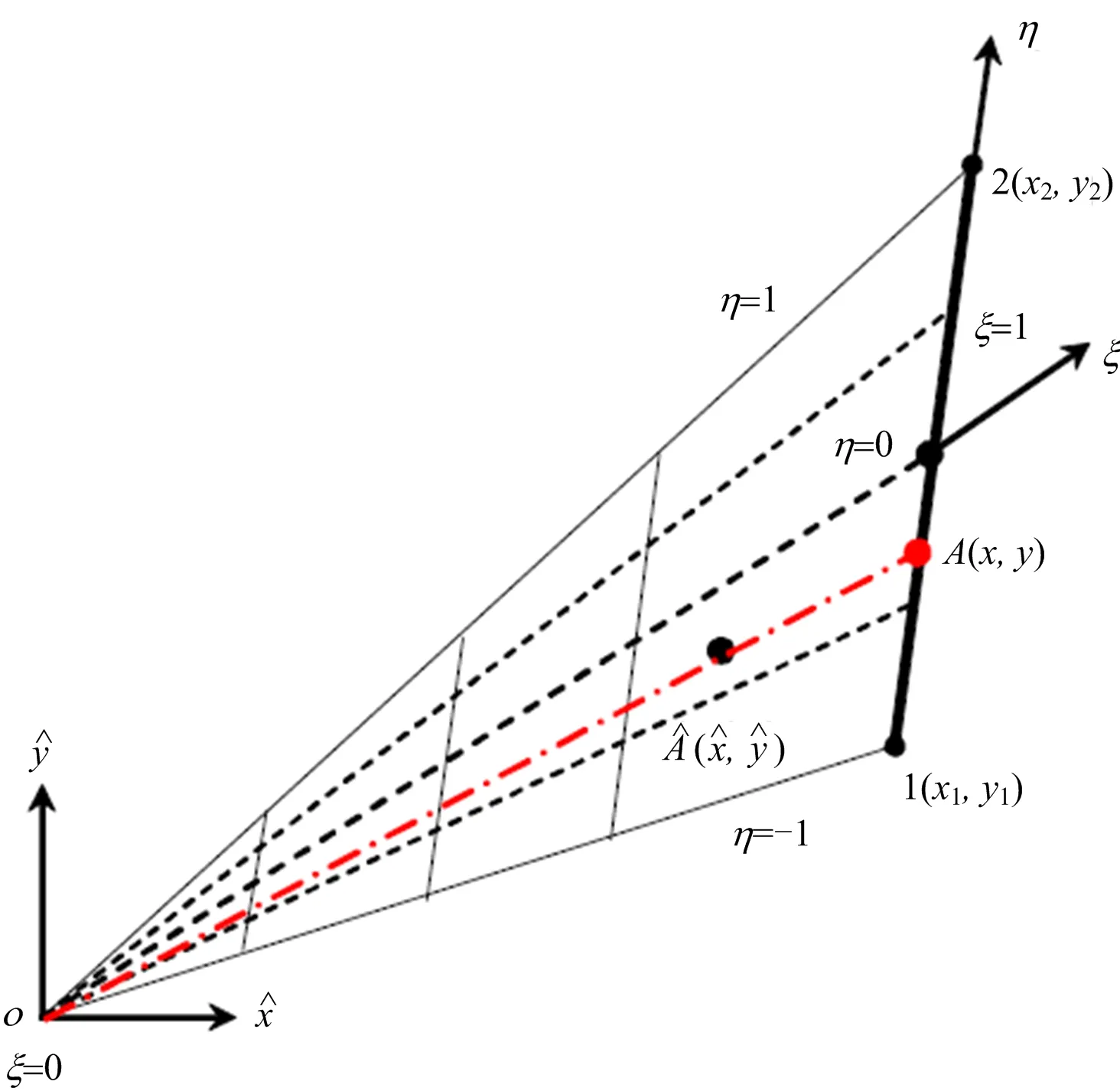
图2　比例边界坐标系下的线单元

转换关系被称作比例边界转换。

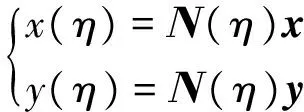
(3)

式中：Ν(η)=[N1(η)N2(η)N3(η)…]为形函数矩阵；x和y分别为离散单元节点的直角坐标矩阵。

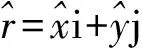
(4)

由此可得单元的Jacobian矩阵为

(5)

其中，

则直角坐标系与比例坐标系下导数之间存在以下关系：

(6)

1.2　频域—波数域控制方程

(7)

其中，

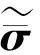
对于各向同性的饱和土体，应力σ、应变ε与位移矢量u满足胡克定律，即

σ=Dε=DLu

(8)

式中：D为饱和土体材料弹性矩阵。

由式(3)和式(7)可知，在图2所示的比例边界坐标系(ξ,o,η)下，频域—波数域微分算子L表示为

(9)

其中，

由式(9)可知，b1，b2与径向坐标为ξ无关，且满足下式：

(10)

对于如图2所示的计算单元中，在ξ=1的边界上，离散节点的位移采用与节点坐标相类似的形函数N表示，则在任一径向坐标ξ处的位移可表示为

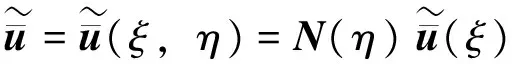
(11)

由式(8)、式(9)和式(11)可知，比例边界坐标系下的应力为

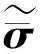
(12)

(13)

其中，

B1=b1N

B2=b2N,η

B3=b3N

由此可知：B1，B2，B3只是环向坐标η的函数，与径向坐标为ξ无关。

(14)

2　基于加权残值法的频域—波数域比例边界有限元方程

2.1　比例边界有限元法的位移方程

在计算单元域内采用伽辽金加权余量法[19-20]，权函数w选取与离散节点位移相同形式的插值形函数，即w=w(ξ,η)=N(η)w(ξ)，对土体动力平衡方程式(14)，在计算域内由伽辽金法可得

(15)

对于式(15)中的第2项，利用分部积分，并将式(4)、式(10)代入后，可得

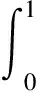
(16)

再将wT=[w(ξ)]TNT代入式(16)，同时要使式(16)在整个积分域成立，则有

(17)

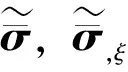
(18)

由此可得由位移形式表示的比例边界有限元方程为

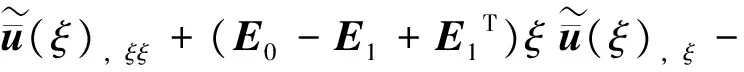
(19)

其中，

2.2　频域—波数域动力刚度

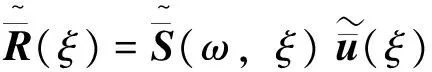
(20)

利用虚功原理，对于ξ为某个常数时所表征的线单元节点力为

(21)

将式(20)代入式(21)，并对ξ求导，再在两端乘ξ并与式(19)相加后可得

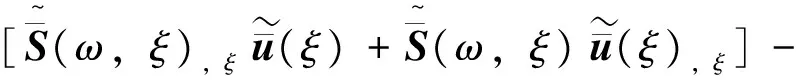
(22)

由上式可得

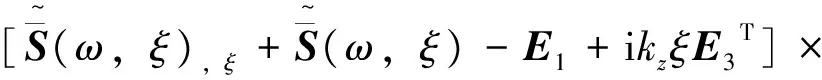
ξ2[ω2M0+(ikz)2E5]+

ikz(E4T-E4)ξ-E2=0

(23)

由文献[23]无量纲分析，并令ξ=1，可得到关于频域—波数域动力刚度方程为

(ikz)2E5+ikz(E4T-E4)-E2=0

(24)

3　数值分析与算例

时间—空间域的动力刚度S(x,y,z,t)可由傅里叶积分逆变换得到，即

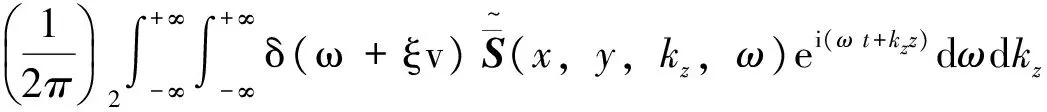
(25)

考虑到Dirac—δ函数特性，则有

(26)

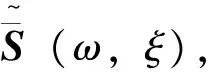
(27)

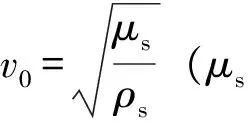
图3　无限空间在r=1.5rt处土体的动力响应

利用本文方法，分析半无限弹性空间中地铁隧道在移动荷载作用下的动力响应。地铁隧道横截面如图4所示，其中圆形半径rt=4.0 m，埋深h=8.0 m。作用在地铁隧道底面的移动荷载分布长度a=2.0 m。土体参数为：泊松比νs=0.3，密度ρs=2.5×103kg·m-3，Lame常量λs=4.0×107N·m-2。为避免奇点对傅里叶积分逆变换的影响，Lame常量取复数，即λs=λs0(1+iζ)， 其中阻尼比ζ=0.01，同样，傅里叶积分逆变换的积分点N=1 025。

根据比例边界有限元方法相似中心的确定原则，对于图4中的半无限域中地铁隧道计算模型，采用文献[23]的子结构分区法，如图4所示，计算域划分为半无限域Ⅰ区，有限域Ⅱ，Ⅲ，Ⅳ区，各区的比例中心点分别为o，o2，o3，o4，半无限域Ⅰ区只在边界DA，AB，BC上采用等参线单元进行离散，离散单元数分别为24，32，24。有限域Ⅱ区边界DC与EF的2D等参线单元离散数为32，CF与DE边的2D等参线单元离散数为12；Ⅲ和Ⅳ区中AE，EP3，BF，FP3边的2D等参线单元离散数均为12，AP3和BP3边的2D等参线单元离散数均为18。

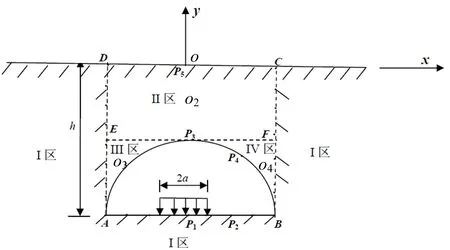
图4　半无限弹性空间中地铁隧道横截面图

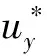
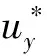
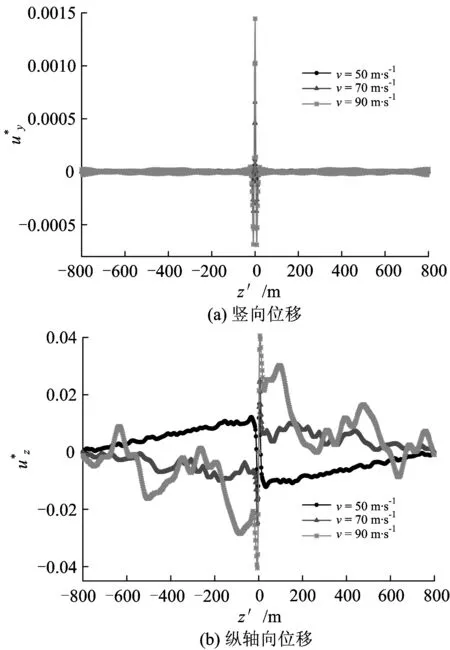
图5不同荷载速度下半无限弹性空间土体中观察点P1的动力响应

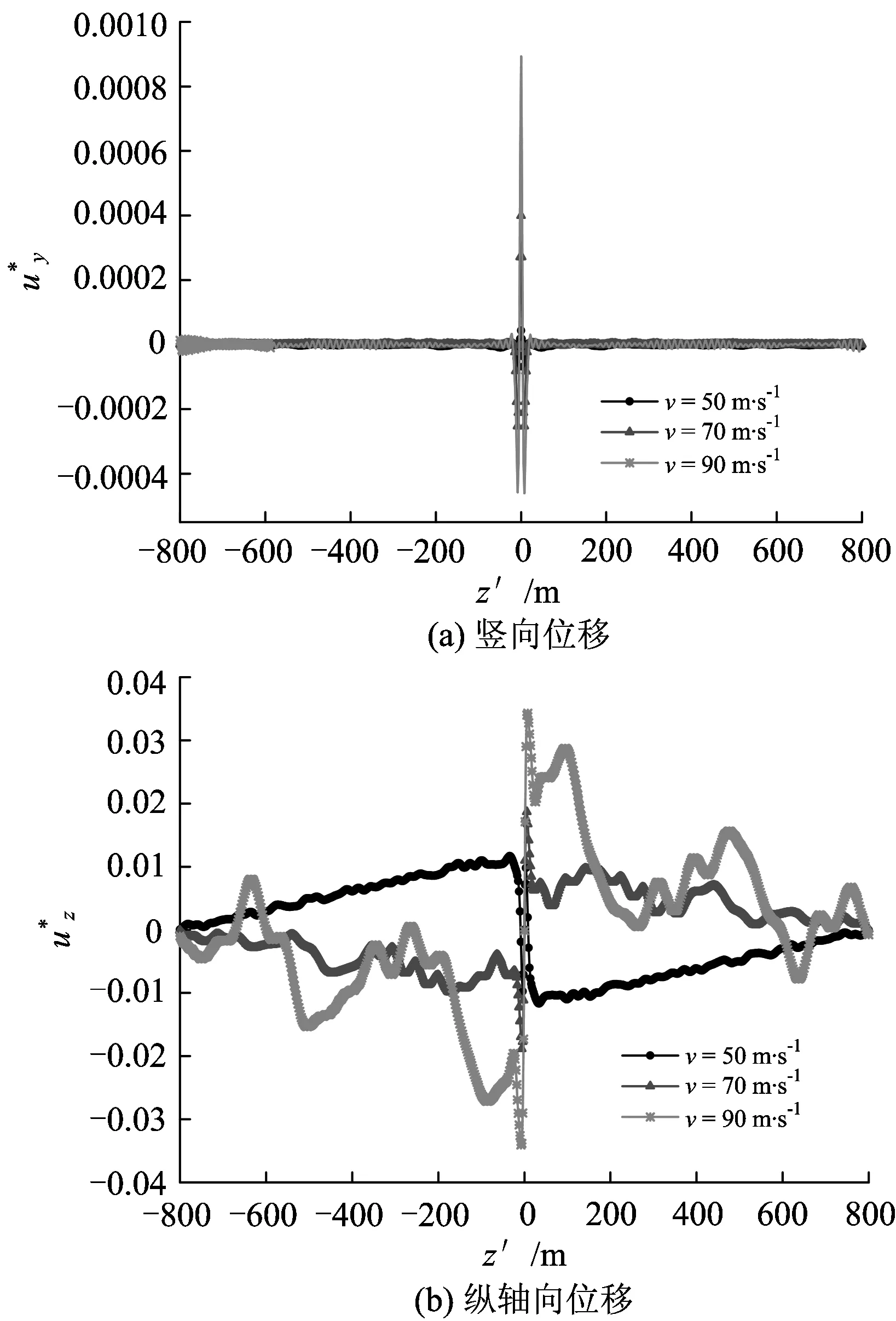
图6不同荷载速度下半无限弹性空间土体中观察点P2的动力响应

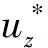
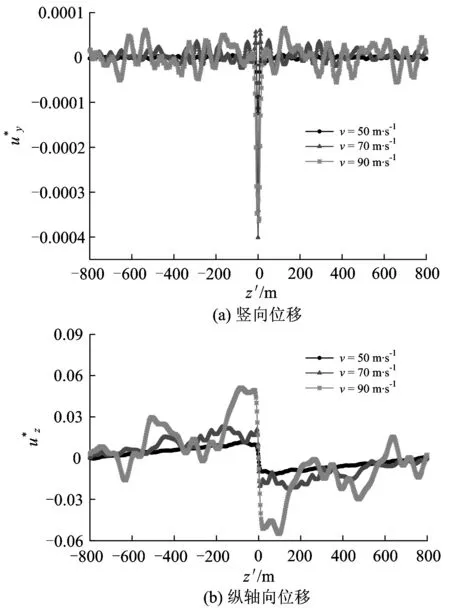
图7不同荷载速度下半无限弹性空间土体中观察点P3的动力响应

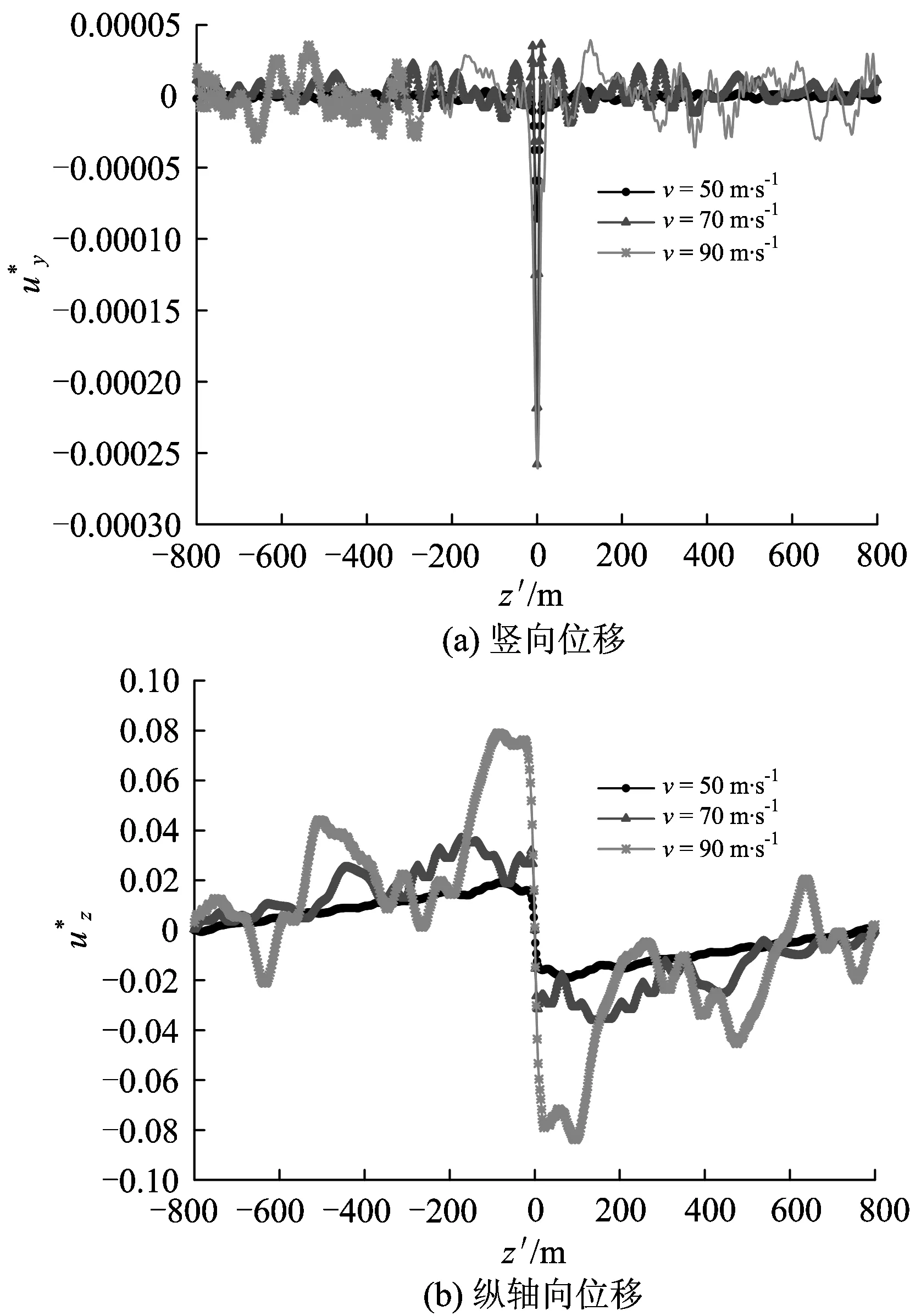
图8不同荷载速度下半无限弹性空间土体中观察点P4的动力响应

(4)对于点P5：在荷载速度较低(v=50 m·

图9不同荷载速度下半无限弹性空间土体中观察点P5的动力响应的

4　结　论

(1) 考虑荷载移动与结构特性，提出在频域—波数域建立比例边界有限元方程，利用时间—空间到频域—波数域的积分变换，可使3D的移动荷载问题转化为2D平面内分析；采用比例边界有限元法，在地铁隧道横截面环向上采用有限元法意义离散，而在具有无穷远的径向，利用比例边界元法，可得到准确的解析解，避免无穷边界计算的误差，同时还可避免边界元法所需的Green函数求解与奇异性问题；

(2) 对于移动荷载作用下的半无限弹性空间，随着荷载移动速度增大，振动波在土体中传播增强，特别是当荷载速度增大到土体剪切波速后，振动波传播到土体表面，引起土体振动显著增大，将会对地铁隧道上部的结构安全性形成一定影响。

(3) 本文方法不仅可解决半无限弹性空间中移动荷载动力响应问题，还可充分利用比例边界有限元的优点，进一步分析半无限弹性空间内具有节理、裂隙等复杂地基的动力响应。

[1]EASON G.The Stress Produced in a Semi-Infinite Solid by a Moving Surface Force[J]. International Journal of Engineering Science, 1965(2): 581-609.

[2]聂志红，刘宝琛，李亮，等.移动荷载作用下轨道路基动力响应分析[J]. 中国铁道科学, 2006, 27(2): 15-19.

(NIE Zhihong，LIU Baochen，LI Liang，et al.Study on the Dynamic Response of the Track/Subgrade under Moving Load[J].China Railway Science, 2006, 27(2): 15-19.in Chinese)

[3]黄晓吉，扶明福，徐斌.移动环形荷载作用下饱和土中圆形衬砌隧洞动力响应研究[J]. 岩土力学,2012,33(3): 892-898.

(HUANG Xiaoji, FU Mingfu, XU Bin. Dynamic Response of a Circular Lining Tunnel in a Saturated Soil Due to Moving Ring Load[J]. Rock and Soil Mechanics, 2012,33(3): 892-898.in Chinese)

[4]贾颖绚，刘维宁，刘卫丰，等.北京地下联络线运营列车振动对既有地铁结构的影响[J]. 中国铁道科学, 2008, 29(5): 72-76.

(JIA Yingxuan, LIU Weining，LIU Weifeng, et al.Influence of Vibration on the Existing Metro Structure Induced by Trains Operated on Beijing Underground Connecting Line[J]. China Railway Science, 2008, 29(5): 72-76.in Chinese)

[5]刘卫丰，刘维宁，DEGRANDE G.地铁列车运行引起地表振动的预测模型及其试验验证[J]. 振动工程学报, 2010，23(4)：373-378.

(LIU Weifeng, LIU Weining, DEGRANDE G.Experimental Validation of a Numerical Model for Prediction of Metro Train-Induced Ground-Surface Vibration[J]. Journal of Vibration Engineering，2010，23(4)：373-378.in Chinese)

[6]袁万，蔡袁强，史吏，等. 基于2.5 维有限元饱和土地基中空沟隔振性能研究[J]. 岩土力学, 2013， 34(7): 2111-2118.

(YUAN Wan，CAI Yuanqiang，SHI Li, et al. Study of Vibration-Isolation Efficiency of Open Trench in Saturated Ground by 2.5D Finite Element Method[J]. Rock and Soil Mechanics, 2013, 34(7): 2111-2118.in Chinese)

[7]刘晶波, 吕彦东.结构—地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998, 31(3): 55-64.

(LIU Jingbo, LÜ Yandong.A Direct Method for Analysis of Dynamic Soil-Structure Interaction[J].China Civil Engineering Journal, 1998, 31(3): 55-64.in Chinese)

[8]SMITH W D.A Non-Reflecting Plain Boundary for Wave Propagation Problems[J]. Journal of Computational Physics, 1974, 15(4):492-503.

[9]ENGQUIST B,MAJDA A.Absorbing Boundary Conditions for the Numerical Simulation Waves[J]. Mathematics of Computation, 1977, 31(139): 629-651.

[10]郭维，周宏业.土—结动力相互作用研究[J]. 中国铁道科学, 2001,22(4): 77-83.

(GUO Wei，ZHOU Hongye.Study on Soil-Structure Interaction[J]. China Railway Science, 2001,22(4): 77-83.in Chinese)

[11]LIAO Z P, ZHOU Z H, ZHANG Y H.Stable Implementation of Transmitting Boundary in Numerical Simulation of Wave Motion[J]. Acta Geophysica Sinica, 2002, 45(4):554-568.

[12]KEYS R G.Local Absorbing Boundary Conditions for Acoustic Media[J].Geophysics, 1985, 60(5): 892-902.

[13]WOLF J P, SONG C H.Doubly Asymptotic Multidirectional Transmitting Boundary for Dynamic Unbounded Medium-Structure-Interaction Analysis[J]. Earthquake Engineering and Structural Dynamics, 1995, 24(2): 175-188.

[14]ANDERSEN L, NIELSEN SRK.Boundary Element Analysis of the Steady-State Response of an Elastic Half-Space to a Moving Force on Its Surface[J]. Engineering Analysis with Boundary Elements, 2003, 27:23-38.

[15]RASMUSSEN KM, NIELSEN SRK, KIRKEGAARD PH.Boundary Element Method in Time Domain for a Moving Time-Dependent Force[J]. Computer Structure, 2001, 79: 691-701.

[16]徐斌，雷晓燕，徐满清，等.饱和土体中空沟对移动荷载被动隔振的2.5D边界元法分析[J]. 岩土力学, 2012, 33(4): 1079-1086.

(XU Bin, LEI Xiaoyan, XU Manqing, et al. Analysis of Effectiveness of Passive Isolation for Vibration Due to a Moving Load on Saturated Soil by Using Open Trench with 2.5D Boundary Element Method[J]. Rock and Soil Mechanics, 2012, 33(4): 1079-1086.in Chinese)

[17]SHENG X, JONES C J C, THOMPSON D J. Prediction of Ground Vibration from Trains Using the Wavenumber Finite and Boundary Element Method[J]. Journal of Sound and Vibration, 2006, 293(3): 575-586.

[18]ANDERSEN L，JONES C J C.Coupled Boundary and Finite Element Analysis of Vibration from Railway Tunnels—a Comparison of Two and Three Dimensional Models[J].Journal of Sound and Vibration, 2006, 293(3): 575-586.

[19]WOLF J P, SONG C M.Dynamic-Stiffness Matrix in Time Domain of Unbounded Medium by Infinitesimal Finite-Element Cell Method[J]. Earthquake Engineering and Structural Dynamics, 1994, 23: 1181-1198.

[20]SONG C M, WOLF J P.The Scaled Boundary Finite-Element Method Alias Consistent Infinitesimal Finite-Element Cell Method[J].Computer Methods in Applied Mechanics and Engineering, 1997, 147(3/4): 329-355.

[21]LI M, ZHANG H, GUAN H, et al.Three-Dimensional Investigation of Wave-Pile Group Interaction Using the Scaled Boundary Finite Element Method. Part I: Theoretical Developments[J]. Ocean Engineering, 2013, 63: 174-184.

[22]SONG H, TAO L.An Efficient Scaled Boundary FEM Model for Wave Interaction with a Nonuniform Porous Cylinder[J]. International Journal for Numerical Methods in Fluids, 2010,63: 96-118.

[23]WOLF J P. The Scaled Boundary Finite Element Method[M]. Hoboken：John Wiley & Sons Ltd, 2003.

[24]OPPENHEIM A V, SCHAFER R W.Discrete-Time Signal Processing[M]. London：Prentice Hall, 1999.