高速铁路隧道基底混凝土结构的随机损伤模型

王志伟，赵有明，张千里，马伟斌，马超锋

(1. 中国铁道科学研究院 研究生部，北京　100081；2. 中国铁道科学研究院 铁道建筑研究所， 北京　100081；3.中国铁道科学研究院，北京　100081)

高速铁路隧道多采用板式无砟轨道结构型式，整体刚度大，不利于振动波衰减，传递到隧道结构的振动强度要比在有碴轨道条件下大，这就要求隧底结构必须具有更高的动力稳定性。然而隧底混凝土作为一种多相复合材料，天然具有随机分布的微空洞、微裂隙等初始损伤，加之施工过程中灌筑、捣固和养护受空间与时间限制，初始损伤更为明显，在高周频率动载作用下，损伤累积使得基底混凝土破坏时有发生，影响行车安全与运营效率。

隧底结构劣化及病害源于尚未掌握基底混凝土自初始受力至破坏全过程的力学行为特性，根本原因在于对新型结构和荷载作用下含初始损伤的基底混凝土应力—应变关系研究不足。目前针对高铁隧道基底结构受荷特性及致灾机理方面的研究，多侧重混凝土力学行为的非线性及荷载响应机制研究[1-5]，所用到的本构模型多针对混凝土破坏时的非线性与强度劣化特征。

实际上，高速铁路隧道基底建设期间，混凝土的配合比、组分等是相同的，其所受外荷载及其他外界影响也无明显差异性，然而基底混凝土结构的破坏在轴线方向呈现出具有随机性与统计学特征。究其原因，在于混凝土的组分及各组分的物理力学性质具有随机分布特征，混凝土材料内部存在具有随机分布特征的微裂纹、微孔洞。这些微观特征必然影响混凝土损伤、破坏的演化进程。表现在宏观上就是混凝土力学性能具有明显的随机性。李杰[6]等也指出，由于混凝土材料组分随机分布的特点，使得初始损伤分布与后续演化过程具有不可忽视的随机分布特征。因此，表征高铁隧底混凝土应力—应变关系的本构模型应该同时反映受力行为的非线性和随机性。

本文采用混凝土随机损伤理论，依据能变量理论、热力学定理，基于改进的塑性亥姆霍兹自由能及能量耗散原理，推导高铁隧底混凝土随机损伤本构模型，引入能量等效应变概念，在有效应力空间建立损伤演化法则与损伤准则，采用二次编程纳入计算软件，通过对比混凝土的单轴拉伸、单轴压缩试验结果与数值计算结果，验证模型的有效性。

1　基于修正的弹塑性亥姆霍兹自由能的随机损伤本构模型

1.1　隧底混凝土结构受力状态

混凝土在复杂应力作用下的破坏形态一般可概括为3种：拉伸破坏、压缩破坏、高静水压力下的压碎破坏。中国铁道科学研究院通过对典型隧道基底应力—应变测试(见图1)，得出隧道底部仰拱混凝土的应力经历了拉—压—拉—压的反复变化(见图2和图3)，因此损伤变量的选取应区分受拉损伤与受压损伤。

图1　隧道基底受荷测试横断面布置图

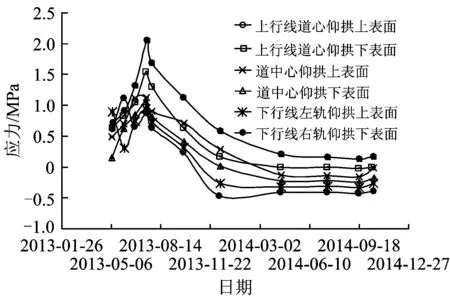
图2　Ⅴ级围岩条件下隧道基底典型部位应力时程曲线

图3　Ⅳ级围岩条件下隧道基底典型部位应力时程曲线

隧道基底采用C25及以上标号的混凝土，而C25混凝土的抗压强度与抗拉强度设计值分别为11.9和1.27 MPa，由图2及图3知，压应力测试结果的最大值小于3 MPa，拉应力测试结果的最大值小于0.5 MPa，可见在不考虑高静水压力导致的应变强化的前提下，隧底混凝土材料的损伤和破坏主要源于受拉损伤和塑压损伤，故需计算列车动载作用下单次振动引起的损伤，分析整个运营期累计损伤对隧道基底混凝土结构寿命的影响。

1.2　热力学基本原理与损伤本构模型基本方程

由于混凝土微开裂不能愈合，且必然伴随能量耗散，故可基于损伤能量耗散过程的不可逆性，建立本构模型。

热力学第一定律指出，系统内动能和内能关于时间的变化率等于外力所做功的功率与外界输送给系统的热能变化率之和，其微分形式可表示为

(1)

不可逆的热力学系统(热力学第二系统)中存在表征热力学温度和熵的单值函数，常用式(2)所示Clausius-Duhem耗散能不等式反映能量耗散与温度梯度的关系。

(2)

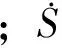
以熵函数作为自由能判据时，要求同时考虑体系和环境的熵变，但由于热力学反应通常都是在等温、等压或等温、等容条件下进行，若能利用这种条件下系统自身状态函数的变化值来判断反应的方向和限度，则要比熵判据方便得多。亥姆霍兹(Von Helmholtz，H.L.P)定义了新的状态函数式为

Ψ≡U-TS=ρ(e-TS)

(3)

式中：Ψ为亥姆霍兹自由能；U为系统的内能，其物理意义为等温可逆过程中，体系对外所做的最大功等于体系亥姆霍兹自由能的减小值。

对于等温纯力学过程，温度函数T为常数且不考虑内部热源q和热流h的影响，热力学第一定律式(1)和热力学第二定律式(2)可分别简化为

(4)

(5)

由于温度函数T为常数，式(3)的微分形式为

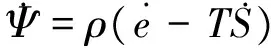
(6)

则式(4)、式(5)可统一写成为

(7)

由式(7)可知，外力所做功的一部分转换为亥姆霍兹自由能，一部分用于变形过程中能量耗散，且其大小为非负值。

定义：D为损伤变量，其表示亥姆霍兹自由能损失的程度；D+为混凝土受拉时亥姆霍兹自由能损失的程度，称为受拉损伤变量；D-为受压时亥姆霍兹自由能损失的程度，称为受压损伤变量。由于混凝土的损伤破坏为一个不可逆的热力学过程，破坏过程产生应变且伴随能量耗散，若仅考虑等温纯力学过程，则亥姆霍兹自由能为有效应变张量ε和损伤变量的状态函数，即

Ψ=Ψ(ε,D)

(8)

将式(8)代入式(7)得

(9)

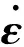
(10)

(11)

由式(10)得

(12)

式(12)含有损伤变量D及有效应变张量ε的应力—应变关系，即损伤力学本构模型基本方程。引入损伤演化方程，根据最大耗散能原理[6]可给出损伤发展方程为

(13)

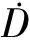
1.3　修正的弹塑性亥姆霍兹自由能

将有效应变张量ε分解为弹性应变张量εe与塑性应变张量εp，有ε=εe+εp。在等温状态下，假设材料的弹性亥姆霍兹自由能势Ψe与塑性亥姆霍兹自由能势Ψp不耦合，则材料的总弹塑性亥姆霍兹自由能势Ψ可以表示为二者之和，即

Ψ(εe,κ,D+,D-)=Ψe(εe,D+,D-)+

Ψp(κ,D+,D-)

(14)

其中，

Ψe(εe,D+,D-)=Ψe+(εe,D+)+Ψe-(εe,D-)

(15)

Ψe+(εe,D+)=(1-D+)Ψe+(ε)

(16)

Ψe-(εe,D-)=(1-D-)Ψe-(ε)

(17)

Ψp(κ,D+,D-)=Ψp+(κ,D+)+Ψp-(κ,D-)

(18)

(19)

(20)

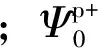
定义：vk表征热力学系统内部状态的变化，fk表示与之相应的广义力变量(伴随变量)。若ε和T表示状态变量，则对应的伴随变量为应力σ和熵S。若内部状态变量选择弹性应变εe、塑性应变εp、累积塑性应变q和损伤变量D，则相应的共轭变量为σ、屈服面半径为R和损伤能量释放率为β。文献[7]指出，当Ψ是ε，D和vk的函数时，热力学第一定律、第二定律可分别写成

(21)

(22)

由于热力学定律对于任何应变速率和温度变化率都成立，则保证式(21)与式(22)成立的必要条件为

(23)

式(23)可等效变换为

(24)

其中，

(25)

(26)

(27)

(28)

q20=q0(0)

(29)

式中：l(q)为硬化函数；fcs为单轴压缩初始屈服应力；fc为单轴压缩强度；q0为初始塑性累计应变；q10和q20分别为单轴压缩、双轴等强度压缩条件下峰值应力所对应的等效塑性应变值。

将式(14)求导，并将式(24)中的3个等式代入有

(30)

将能量释放率弹塑性解耦，有

β±=βe±+βp±=Ψe0±+Ψp0±

(31)

式中：Ψe0±和Ψp0±分别为初始弹性亥姆霍兹自由能与初始塑性亥姆霍兹自由能，数值上分别等于能量释放率的弹性部分与塑性部分。

Faria等[8]指出Ψe0±用下式计算：

(32)

式中：C0为初始柔度张量。

(33)

则式(19)变为

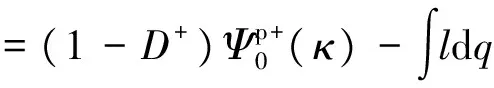
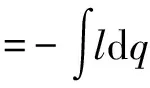
(34)

联立式(14)—式(18)、式(20)、式(34)可得修正后的弹塑性亥姆霍兹自由能为

Ψ(εe,κ,D+,D-)=Ψe(εe,D+,D-)+

(35)

1.4　随机损伤本构模型

材料的损伤本构关系可由热力学定律的统一公式(7)导出，将式(35)关于时间微分，并代入式(7)，可得

(36)

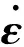
(37)

将式(15)代入式(37)，可得

(38)

进而将式(16)代入式(38)，即可得到弹塑性随机损伤本构关系为

σ=(1-D+)σ++(1-D-)σ-

=(1-D):σ=(1-D)E0:(ε-εp)

(39)

其中，

D=D+P++D-P-

(40)

(41)

P-=I-P+

(42)

在二维平面应力状态下，损伤发展导致混凝土各向异性，宜将对应的割线刚度矩阵做对称化处理，根据式(39)可分别得到双轴拉压状态下主应力方向的随机损伤应力—应变关系式为

(43)

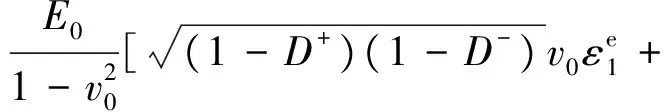
(44)

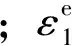
隧道底部混凝土受拉损伤与受压损伤细观破坏都有随机不可控性质，损伤变量在数学意义上是随机变量，存在概率密度分布、均质与标准差等概率描述。由于损伤演化非常复杂，故可以通过取损伤均值，建立随机损伤与确定性损伤之间的联系。李杰等[6]给出混凝土受拉损伤和受压损伤的均质与方差统一表达式为

(45)

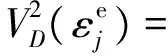
(46)

损伤准则是判断损伤是否发生的一个依据，损伤破坏的过程本身就是一种平衡和稳定被随时打破而又随时建立起来的一种过程，因此最小耗能原理也适用于损伤准则的建立。当已知耗能系统的能量耗散率及此过程所必须满足的约束条件，则可以找到满足系统耗能取驻值的条件，由此可建立统一形式的损伤准则。塑性理论的流动法则可以写为

(47)

考虑损伤系统的能量耗散由损伤耗能ΘD和塑性耗能Θp两种机制产生，因此总耗能Θ为

(48)

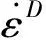
损伤过程的能量耗散要受到损伤准则G(σ)=0的约束，据耗能极值原理，取极值的条件应满足：

(49)

式中：ϑ为拉格朗日(Lagrange)乘子；G为损伤准则。

将式(48)代入到耗能取驻值的条件式(49)中可得

(50)

式中：相对变量σ而言，C0的数学意义为积分常数，物理意义为损伤D对G的影响，是与损伤门槛值相关的参量。

式(50)在对σ积分时，若将D固定，即认为D独立于σ，可得

G(σ)=β-β0

(51)

其中，

(52)

(53)

式中：β0为损伤因子阀值，物理意义为控制损伤面的发展。

损伤理论的核心问题是确定损伤演化规律，即损伤变量D随其他内变量变化而变化的规律。由式(47)所示损伤准则，根据正交流动法则，可以得到损伤变量的演化法则为

(54)

(55)

式中：上角标为“+”、“-”分别表示受拉与受压状态。

损伤加卸载条件即Kuhn-Tucker关系为

(56)

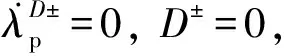
(57)

(58)

因此，只要给定函数G±的具体表达式，损伤变量可以根据式(58)求得

(59)

(60)

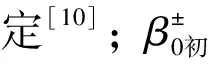
(61)

式中：Δ取值范围为1.1～1.2。

2　随机损伤本构模型数值实现

由于塑性演化与损伤分别发生在有效应力空间与损伤空间，二者解耦，故应力更新过程可采用Simó和Ju等[10]建议的算子分离算法。本构模型数值实现遵循“弹性预测—塑性修正—损伤修正”思路，计算流程如图4所示。

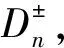
(62)

将式(62)代入屈服函数f中，若tn+1时刻预测屈服函数满足式(63)：

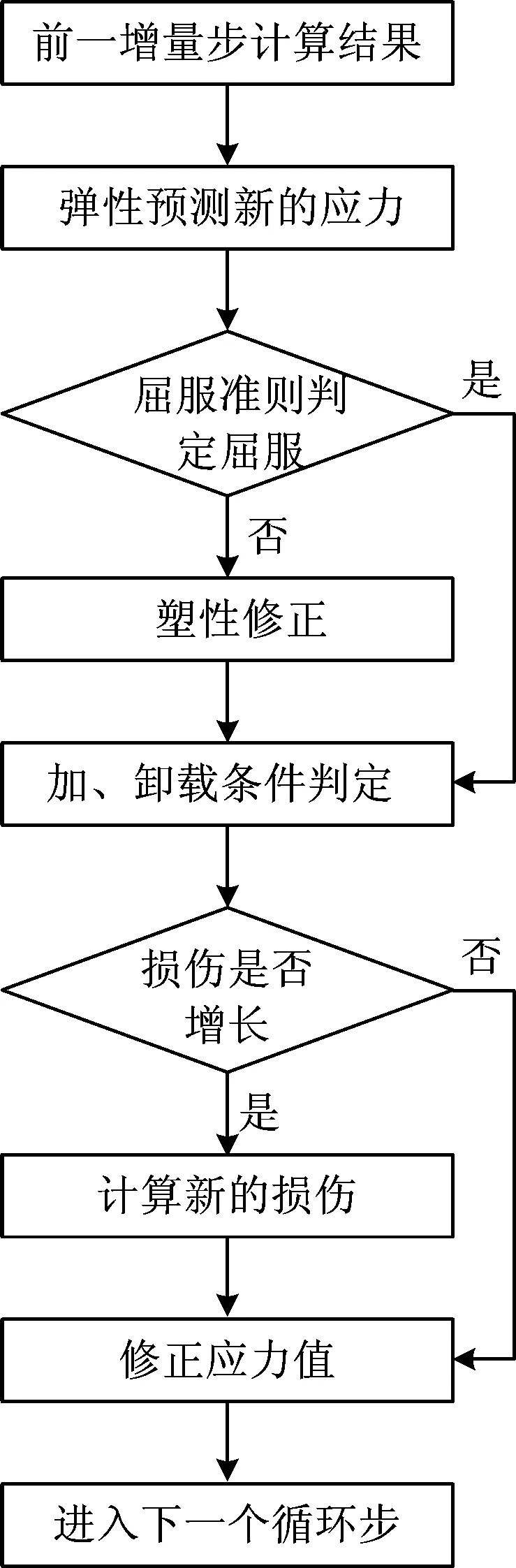
图4　本构模型数值实现流程

(63)

则增量步[tn,tn+1]内有塑性流动产生，即不满足屈服准则，应进行塑性修正。由于有效应力空间塑性状态与损伤无关，可采用回映算法[11]实现，按式(64)进行塑性修正。

(64)

(65)

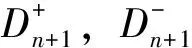
混凝土初始损伤的随机性对其受力破坏非线性的影响涉及随机性在物理系统中的传播。李杰等[12]考察了随机事件状态转移过程中的概率守恒原理，建立了一般随机系统的广义概率密度演化方程，形成了随机非线性分析的一般理论。本文采用这一思想，令Z为概率系统，G为概率函数，Υ为反映结构材料性质的随机损伤变量，Γ为结构加载参数，x为决定结构反应所在位置的空间位置变量，则一般加载条件下结构的非线性反应可表述为[6]

Z=G(Υ,Γ,x)

(66)

对于式(66)存在式(67)所示可应用于随机损伤本构的关系式，计算应力关于应变的概率密度演化进程。

(67)

广义概率密度演化方程的求解可以采用有限差分方法[14]。李杰和陈建兵[15]给出了非线性随机反应求解步骤。在概率密度演化方程求解的基础上，本文借助于有限差分软件FLAC3D所提供的二次开发程序接口，采用C++语言编写计算程序，实现本构模型的程序化计算。FLAC(Fast Lagrangian Analysis for Ceontinua，连续介质快速拉格朗日分析)有限差分程序是一种利用拖带坐标系分析大变形问题的数值方法，它采用差分格式按时步积分求解，随构形的不断变化，不断更新坐标，允许介质有较大变形，其计算流程如图5所示。

图5　FLAC计算循环过程

本构模型二次开发过程也就是继承FLAC3D软件自带的Constitutive Model基类，并重载其中的2个关键函数：Initialize()函数和Run()函数。由于屈服准则和拉、压损伤组合系数表示为主应力或主应力不变量的形式，所以在每个循环步中需要得到单元主应力值，这一任务由程序中的Resoltopris()和Resoltoglob()这2个重要函数完成。基于该本构模型开发的程序流程如图6所示。

3　随机损伤本构模型数值验证

图6　损伤本构程序开发流程图

对于拉伸试验，采用数值模拟分析应力均值加减1倍均方差范围时的应力—应变全过程曲线；对于压缩试验，采用数值模拟分析应力均值加减1倍、加减2倍均方差范围时的应力—应变全过程曲线。模拟结果与试验结果对比如图7和图8所示。

图7　单轴拉伸应力—应变全过程曲线

由图7和图8可知：数值模拟结果与试验结果较为一致，说明开发的损伤本构模型可以较为准确地模拟混凝土受拉、受压条件下的应变软化过程；试验点落在应力均值加减1倍或2倍均方差范围之内，说明开发的损伤本构模型不仅可以在均值意义上反映混凝土受拉、受压的应力—应变关系，也可以在概率意义上模拟其离散范围，可较为全面地反映混凝土受力行为的非线性与随机性。

图8　单轴压缩应力—应变全过程曲线

4　工程案例

4.1　高铁隧道结构型式与动力荷载

高速铁路隧道一般采用：三心圆曲墙双线隧道，Ⅴ级围岩，设计行车速度为350 km·h-1，排水型复合式衬砌。代表性的隧道衬砌结构断面如图9所示。列车荷载涉及列车轴重、悬挂质量、行车速度、轨道组成、线路平顺等因素，本文采用文献[17]中的加载方法。

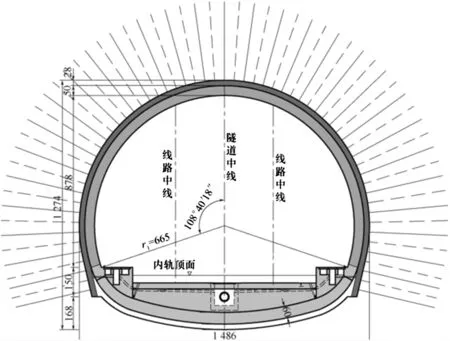
图9　代表性的隧道衬砌结构断面(单位：cm)

4.2　模型计算参数与计算步骤

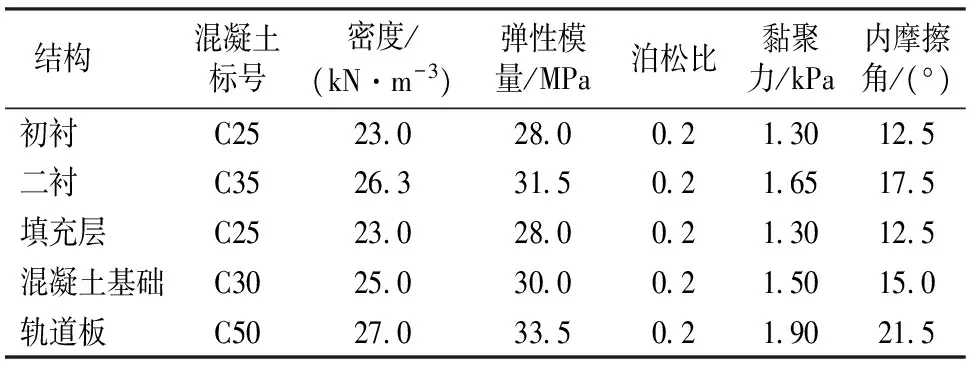
地层为四节点平面应变单元，材料特性采用弹塑性增量本构模型模拟，地层材料参数见表1。初衬、二衬、填充层、混凝土基础、轨道板均采用四节点平面单元，材料物理力学参数见表2，材料特性采用本文所提出的随机损伤本构模型模拟，损伤模型计算参数由混凝土单轴受拉试验与单轴受压试验标定得到[17]，结果见表3。锚杆对围岩的加固作用通过提高锚固区围岩参数模拟。模型左侧、右侧、下侧各取4倍隧道跨度，上部埋深为20 m，由此建立的有限差分模型局部网格模型如图10所示。

计算步骤分为：建模→划分网格→定义静力边界(两侧水平位移固定，底部竖向位移固定)→开挖(上、下两台阶开挖)→支护→动力边界→动力计算。

表1　Ⅴ级围岩地层物理力学参数

表2初衬、二衬、填充层、混凝土基础、轨道板物理力学参数

结构　　混凝土标号密度/(kN·m-3)弹性模量/MPa泊松比黏聚力/kPa内摩擦角/(°)初衬　　　C2523028002130125二衬　　　C3526331502165175填充层　　C2523028002130125混凝土基础C3025030002150150轨道板　　C5027033502190215

表3二衬、填充层、混凝土基础、轨道板损伤模型计算参数

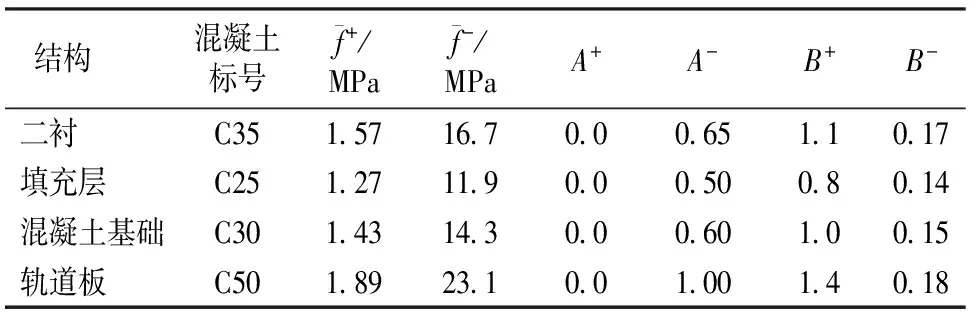
结构　　混凝土标号f+/MPaf-/MPaA+A-B+B-二衬　　　C351571670006511017填充层　　C251271190005008014混凝土基础C301431430006010015轨道板　　C501892310010014018

图10　计算模型局部网格划分

4.3　损伤演化过程及寿命分析

由文献[1]可知，不同行车速度、不同围岩级别条件下仰拱底部为损伤最大的位置，且破坏主要由受拉强度控制，因此选取图10中M点计算分析损伤随时间的演化过程。在模型几何尺寸不变条件下，为与相似研究进行对比，初始损伤量取文献[1]中的值0.050 130 000进行模拟，行车速度分别取200，250， 300 km·h-1，采用本文的随机损伤本构模型和计算程序进行计算。随时间演化的损伤量如图11所示，列车荷载作用下振动一次引起的损伤量如图12所示。

图11　不同行车速度条件下随时间演化的累计损伤量

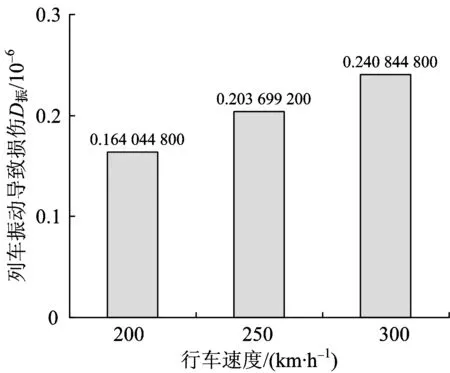
图12不同行车速度时列车荷载作用下振动1次引起的损伤量

由图11和图12可知：4种行车速度条件下的损伤量演化规律基本相同；0.0～0.5 s作用时间内，损伤量急剧增长，瞬间接近最大值，而后损伤量趋于定值；累计损伤量及由列车振动引起的损伤量均随着行车速度的增长而增长；当行车速度为300 km·h-1时，累计损伤量最大值为0.051 747 183，列车荷载作用下振动1次引起的最大损伤量为0.240 844 800×10-6，均远小于1，说明单次列车运行引起的衬砌结构损伤量非常小，对衬砌结构安全几乎无影响。

然而，对于运营期的高速铁路，按照每日开行100对列车，每列车16辆编组，隧道服役期为100年计算，总通过车流量为365×104次，属于高周频率范畴，需进行损伤疲劳寿命分析。采用Palmgren-Miner疲劳累计损伤理论计算公式，即

(68)

根据式(68)可得不同行车速度条件下的疲劳寿命(四舍五入取整)，见表4。由表4可知，采用本文本构模型计算结果与文献1计算结果相对差值最大为8.0%，既证明了本文模型的适用性，也说明Ⅴ级围岩条件下，行车速度小于等于300 km·h-1时，当前高速铁路隧道设计参数可满足设计基准期内抗疲劳要求。

表4基于Palmgren-Miner疲劳累计损伤理论计算的损伤疲劳寿命

行车速度/(km·h-1)D+振/10-6损伤疲劳寿命/a采用本文模型计算结果文献[1]计算结果相对差值/%20001640448001501388025002036992001211136730002408448001029659

需要说明的是，隧道底部直接与列车轮接触的轨道板的受力和损伤要远大于仰拱处的受力和损伤，结构的破坏除损伤引起外，尚与底部累计沉降等有关，结构的破坏及其寿命是多因素综合影响的结果，损伤疲劳仅可供参考。

5　结　论

(1)本文基于现场实测的高铁基底混凝土结构受力“拉—压—拉—压”变化特性，依据内变量理论，分别定义受拉、受压损伤变量，并按照热力学第一、第二定律及能量耗散原理，给出了损伤发展方程式。

(2)为全面反映热力学相容条件，修正了弹塑性亥姆霍兹自由能，并通过弹塑性解耦，推导了基于修正的弹塑性亥姆霍兹自由能的随机损伤本构模型，引入弹塑性损伤能释放率及其阀值，建立了损伤准则，根据弹塑性力学正交流动法则，给出了损伤变量的演化法则。

(3)建立了所提出模型的“弹性预测—塑性修正—损伤修正”数值分析求解框架，采用C++语言编写计算程序，借助于有限差分软件FLAC3D所提供的二次开发程序接口，实现了本构模型的程序化计算。

(4)通过与前人所做混凝土材料单轴拉伸、单轴压缩试验对比，表明本文提出的随机损伤本构模型，一方面可较准确地模拟混凝土受拉、受压条件下的应变软化及非线性特性；另一方面，既可以在均值意义上反映混凝土受拉、受压的应力—应变关系，也可以在概率意义上模拟其离散范围，可较为全面地反映混凝土受力行为的非线性与随机性。

(5)采用本文模型对不同行车速度条件下隧道衬砌结构损伤疲劳寿命进行初步分析可知，Ⅴ级围岩条件下，行车速度小于等于300 km·h-1时，当前高速铁路隧道设计参数可满足设计基准期内抗疲劳的要求。

[1]黄娟. 基于损伤理论的高速铁路隧道结构振动响应分析及疲劳寿命研究[D].长沙：中南大学,2010.

(HUANG Juan. Study on the Vibration Response and Fatigue Life of High-Speed Railway Tunnels Based on Damage Theory[D]. Changsha: Central South University, 2010. in Chinese)

[2]丁祖德. 高速铁路隧道基底软岩动力特性及结构安全性研究[D]. 长沙：中南大学,2012.

(DING Zude. Dynamic Properties of Soft Rock and the Safety of Base Structure of High-Speed Railway Tunnels[D]. Changsha：Central South University, 2012. in Chinese)

[3]蔡斌. 高速铁路隧道基底软岩动力响应及疲劳损伤特性研究[D].广州：广东工业大学,2015.

(CAI Bin. Study on the Characteristics of Dynamic and Fatigue Damage of Soft Rock-Mass for Basement of High Speed Railway’s Tunnel[D]. Guangzhou：Guangdong University of Technology, 2015. in Chinese)

[4]王祥秋,蔡斌,JIANG Ruinian. 高速铁路隧道基底软岩动力累积损伤特性[J]. 土木建筑与环境工程,2015,37(5):26-32.

(WANG Xiangqiu, CAI Bin, JIANG Ruinian. Characteristics of Soft Dynamic and Accumulative Damage of Soft Rock-Mass for the Basement of High Speed Railway's Tunnel[J]. Journal of Civil, Architectural & Environmental Engineering, 2015, 37(5):26-32. in Chinese)

[5]黄娟,彭立敏,李晓英,等. 隧道振动响应研究进展[J]. 中国铁道科学,2009,30(2):60-65.

(HUANG Juan, PENG Limin, LI Xiaoying, et al. Progress Made in the Research on the Vibration Response Induced by Trains Running through Tunnels[J]. China Railway Science, 2009, 30(2):60-65. in Chinese)

[6]李杰,吴建营,陈建兵. 混凝土随机损伤力学[M]. 北京: 科学出版社, 2015.

[7]刘军. 混凝土损伤本构模型研究及其数值实现[D]. 大连：大连理工大学,2012.

(LIU Jun. A Study on the Damage Constitutive Model for Concrete and Its Numerical Implementation[D]. Dalian: Dalian University of Technology,2012. in Chinese)

[8]FARIA R, OLIVR J, CERVERA M. A Strain-Based Plastic Viscous-Damage Model for Massive Concrete Structures [J]. International Journal of Solids and Structures, 1998, 35(14):1533-1558.

[9]WU Jianying, LI Jie, FARIA R. An Energy Release Rate-Based Plastic-Damage Model for Concrete[J]. International Journal of Solids and Structures, 2006, 43(3/4):583-612.

[11]BELYTSCHKO T, LIU W K, MORAN B. Nonlinear Finite Elements for Continua and Structures[M]. New York: John Wiley & Sons Ltd, 2000.

[12]LI Jie, CHEN Jianbing. The Principle of Preservation of Probability and the Generalized Density Evolution Equation[J]. Structure Safety, 2008, 30(1):65-77.

[13]LI Jie, CHEN Jianbing. Stochastic Dynamics of Structures[M]. Singapore: John Wiley and Sons, 2009.

[14]李杰,陈建兵. 随机动力系统中的概率密度演化方程及其研究进展[J]. 力学进展,2010, 40(2):170-188.

(LI Jie, CHEN Jianbing. Advances in the Research on Probability Density Evolution Equations of Stochastic Dynamical Systems[J]. Advances in Mechanics, 2010,40(2):170-188.in Chinese)

[15]GOPALARATNA, V S, SHAH S P. Softening Response of Plain Concrete in Direct Tension[J]. ACI Journal, 1985, 82(3):310-323.

[16]KARSAN I D, JIRSA J O. Behavior of Concrete under Compressive Loading[J]. Journal Structure Division, 1969, 95(12):2543-2564.

[17]杜明庆,张顶立,房倩,等. 铁路隧道仰拱及仰拱填充层动力响应分析[J]. 中国铁道科学,2016,37(3):38-45.

(DU Mingqing, ZHANG Dingli, FANG Qian, et al. Dynamic Response Analysis of Railway Tunnel Invert and Its Filling Layer[J]. China Railway Science, 2016,37(3):38-45.in Chinese)