不同攻角约束下空空导弹敏捷转弯过程弹道优化

彭继平+霍鑫+杨宝庆+董继鹏+张金鹏

摘要： 为考察攻角约束对直气复合控制的导弹实现越肩发射的影响， 首先针对一个反作用喷气系统安装在尾部的敏捷导弹建立了俯仰通道四阶动态模型， 然后利用高斯伪谱法获得时间-燃料最优解， 并对不同攻角约束下的最优解进行了分析和比较。 仿真结果说明攻角约束越严格， 敏捷转弯过程的转弯半径越大， 时间越长， 燃料消耗越多。

关键词： 敏捷转弯； 攻角约束； 高斯伪谱法； 弹道优化

中图分类号： TJ765文献标识码： A文章编号： 1673-5048（2017）01-0039-06[SQ0]

0引言

随着空中作战场景的逐渐升级， 现代空战对空空导弹的机动性和打击能力提出了更严格的要求。 在空中近距格斗中， 具备大离轴角打击能力或

者后半球目标打击能力将具有突出优势[1]。 以离轴发射为基础的全向攻击技术， 使得载机能在目标周围的任意角度上攻击目标， 而越肩发射能够以载机为中心攻击载机周围任意方位的目标， 实现真正意义上的全向攻击[2]。 越肩发射分为后射和前射两种方式： 后射是导弹直接向后发射， 攻击后方目标， 也称“后向攻击”[3-4]； 前射是导弹向前发射， 在空中转弯， 攻击后方目标。 前射需要采用复合制导导弹， 前射过程可以分为敏捷转弯段和末制导段[5]。

在敏捷转弯段， 建立导弹的运动学和动力学模型十分困难， 这是由于在大机动飞行中， 导弹会经历大攻角失速状态， 气动力的强非线性和强耦合变得非常严重[6]。 为解决大攻角飞行气动力不足的问题， 推力矢量控制技术和反作用喷气控制技术被引入， 使推力矢量/气动力、 直接侧向力/气动力的复合控制问题成为一个新的热门研究课题。 Rui Hirokawa 等针对装配了反作用喷气系统的导弹， 利用CDM方法设计了一个自动驾驶系统[7]。 崔彦凯等将变结构控制应用于越肩发射过程中推力矢量与气动力的复合控制， 并取得很好的控制效果[8]。 此外， 敏捷转弯的优化问题也得到一定程度的关注。 聂川义等采用序列二次规划法对空射导弹助推段的弹道进行设计与优化， 有效缩短了弹道优化计算时间， 加快了收敛速度[9]。 鲜勇等提出一种变射面横向机动弹道， 并利用随机方向法和牛顿迭代法相结合的混合优化方法， 实现了机动弹道的优化[10]。

通常， 越肩发射要求导弹具备大攻角飞行的能力， 因而导弹的攻角通常都是默认无约束的， 即攻角大小可在0°～180°范围内变化。 目前尚未有相关文献研究攻角约束对越肩发射过程的影响。 针对以上问题， 本文将研究存在攻角约束的条件下越肩发射敏捷转弯的实现。

1导弹模型建立

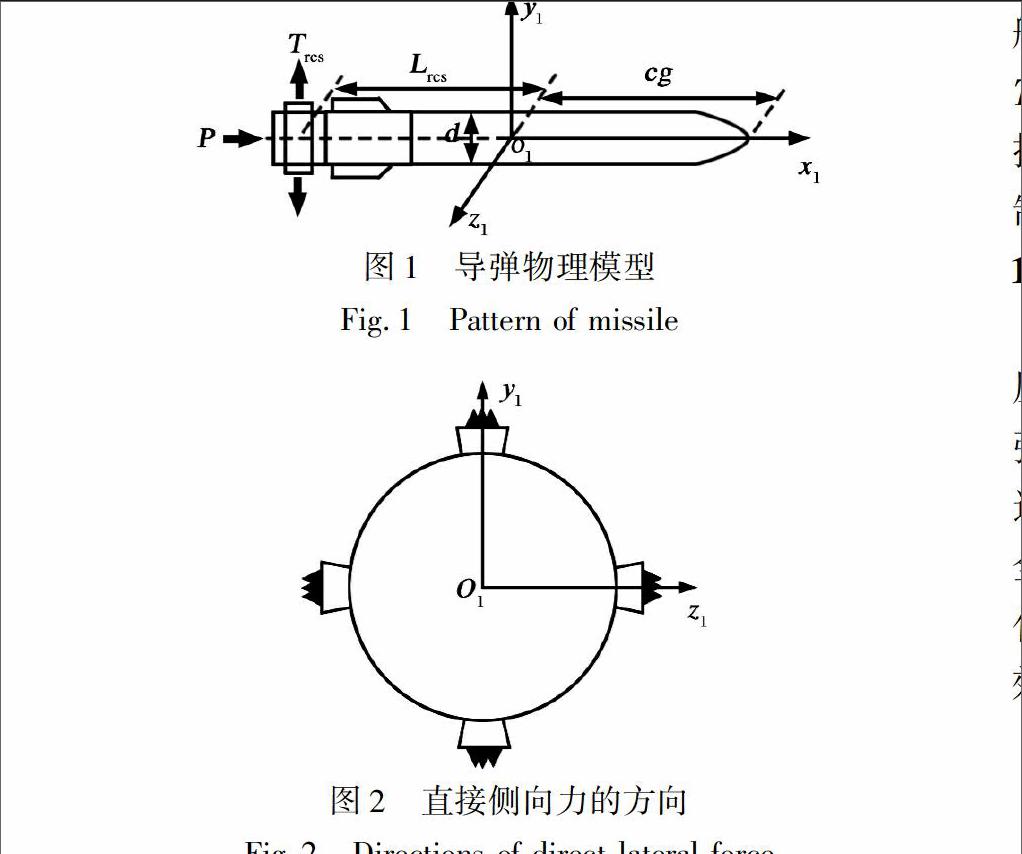
示。 反作用喷气系统安装在导弹尾部。 其中o1x1y1z1为弹体坐标系； cg为导弹质心到弹头的距离； Lrcs

为直接侧向力作用平面到导弹质心的距离； d为弹体直径； P和Trcs分别为导弹主推力和直接侧向力。 为简单起见， 假设反作用喷气系统仅提供四个方向的直接侧向力， 从尾部方向观察的四个直接侧向力的方向， 如图2所示。

为了综合所设计的控制系统， Mario Innocenti等人[11]以一个细长圆柱体为标准， 建立了导弹的几何模型和动力学模型。 本文导弹的基本物理参数都基于Mario Innocenti的研究。 为了简化建模过程， 进行如下假设：

航空兵器2017年第1期

彭继平， 等： 不同攻角约束下空空导弹敏捷转弯过程弹道优化

（1） 忽略导弹的质量变化；

（2） 侧滑角和滚转角均设为零， 即仅考虑导弹的俯仰运动；

（3） 不考虑反作用喷气的喷流干扰效应；

（4） 主推力只能提供沿着弹体纵轴方向的力， 同时发动机的装配误差也不予考虑。

1.1小攻角模型

导弹的气动力参数可以通过DATCOM仿真获得。 但获得的数据只在小攻角（≤35°～40°）飞行条件下才可靠[12]， 因此只能建立导弹的小攻角模型。 导弹在惯性坐标系下的受力分析如图3所示。

3仿真结果及分析

导弹的主要物理参数如表1所示。 通过DATCOM获得的标准细长圆柱体在小攻角飞行条件下导弹的气动力数据如表2所示。 CNα和CNδ分别为法向气动力对攻角和舵偏角的一阶偏导数。 数据对应海拔3 000 m高度的四个不同速度， 运用线性插

值法可估计出导弹在不同速度下的气动力参数。

高斯伪谱法求解导弹的最优控制问题是通过MATLAB工具箱GPOPS-II来实现的。 GPOPS-II是一款求解非线性最优控制的软件， 其在飞机航迹优化、 飞行器轨道再入等方面有着广泛的运用。 仿真过程中取30个点（28个LG点）作为配点。

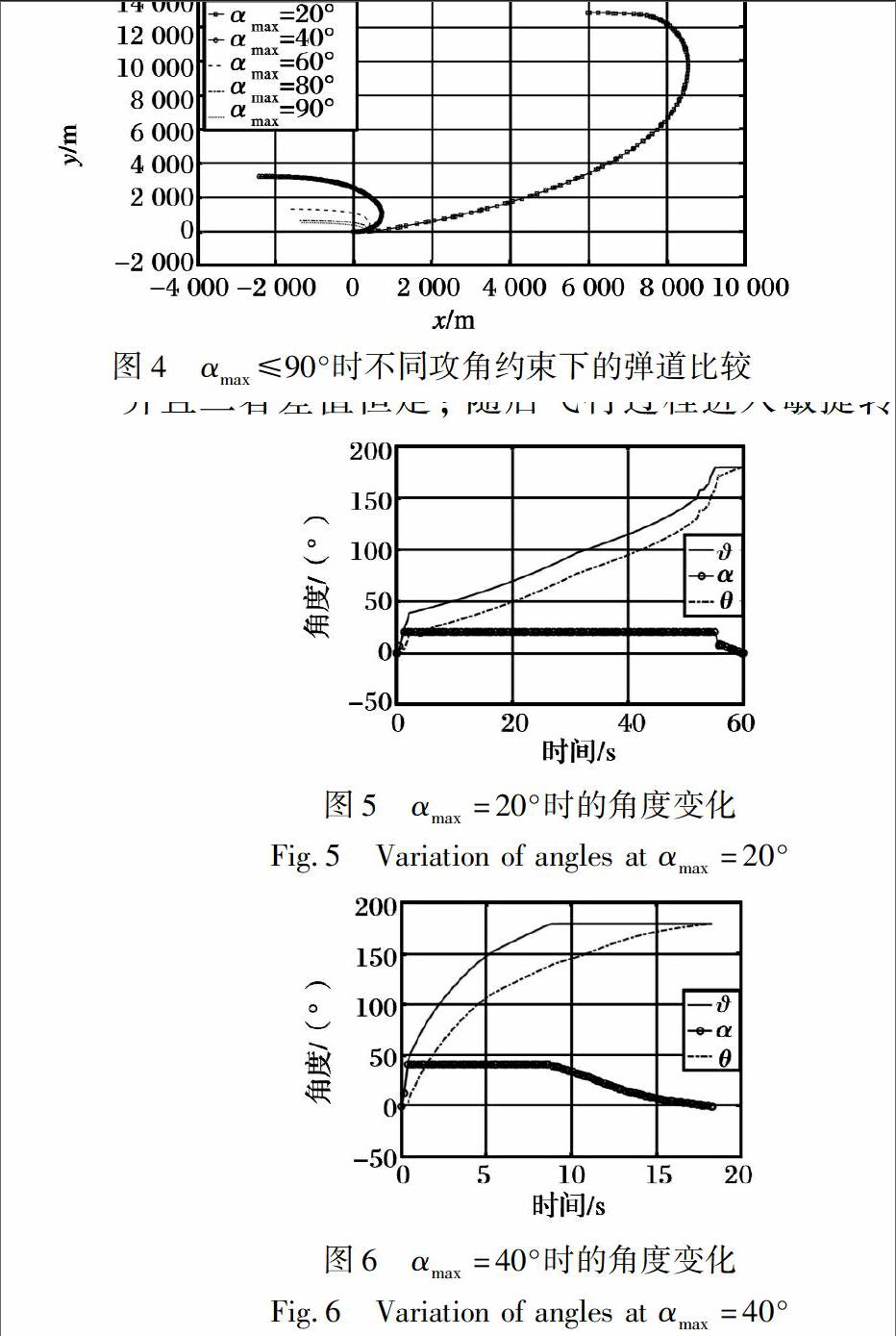
五个不同攻角约束条件下越肩发射过程的俯仰角、 攻角以及弹道倾角的变化曲线如图5～9所示。 从图中可知， 在敏捷转弯开始阶段， 需要快速建立攻角， 由于导弹自身运动的惯性， 速度方向变化明显慢于俯仰角的变化， 因而攻角和俯仰角的变化曲线几乎重合；攻角建立之后， 由于攻角约束的存在， 俯仰角继续增大， 弹道倾角也随之增大， 并且二者差值恒定； 随后飞行过程进入敏捷转弯

为了对能量消耗情况进行侧向说明， 可以从速度的角度进行分析。 不同攻角约束条件下导弹的速度变化曲线如图12所示， 当攻角约束为20°时， 导弹的速度一直增大到最大速度后， 才减速到要求的终端速度；而攻角约束为40°和60°时， 导弹的速度也是一开始就增大然后減小。

αmax越大， υ在开始阶段增速越多， 然而速度的增大需要主发动机的燃料消耗， 这显然造成了不必要的燃料浪费。 当攻角约束为80°和90°时， 导弹速度是先减小的， 说明开始时主推力做功很小甚至

不做功， 从而节省了燃料， 而且αmax越大， 导弹所达到的最低速度值越小， 说明主发动机的燃料消耗越小。

4结论

研究了攻角约束对空空导弹越肩发射敏捷转

弯过程的影响。 建立了导弹在小攻角和大攻角飞行时的俯仰通道动力学模型， 明确了越肩发射的弹道优化问题的必要约束条件， 并利用高斯伪谱法求解出时间-燃料最优的弹道优化问题。 仿真结果给出了不同攻角约束下导弹姿态角变化、 弹道形状、 完成时间以及能量消耗这四个方面的比较。 结果表明， 导弹飞行时所能达到的最大攻角越大， 弹道半径越小， 完成转弯的时间越短， 耗费的燃料越少。 所以导弹若需要尽可能快地实现速度转向， 必须具备一定大攻角飞行的能力。 若导弹在某攻角约束条件飞行时能够满足时间、 能量消耗以及转弯半径的要求， 则可不必追求更强的敏捷性能， 对导弹机动性的设计有着一定的指导意义。

参考文献：

[1] Wise K A， Roy D J B. Agile Missile Dynamics and Control[J]. Journal of Guidance， Control， and Dynamics， 1998， 21（3）： 441-449.

[2] 马登武， 刘琰， 田振华. 空空导弹的越肩发射技术综述[J]. 海军航空工程学院学报， 2007， 22（3）： 377-381.

Ma Dengwu， Liu Yan， Tian Zhenhua. Survey on Over the Shoulder of AirtoAir Missile[J]. Journal of Naval Aeronautical Engineering Institute， 2007， 22（3）： 377-381.（in Chinese）

[3] 高劲松， 陈哨东， 朱荣刚，等. 越肩发射的研究现状和发展[J]. 火力与指挥控制， 2005， 30（8）： 1-5.

Gao Jinsong， Chen Shaodong， Zhu Ronggang， et al. Development on Over the Shoulder[J]. Fire Control & Command Control， 2005， 30（8）： 1-5.（in Chinese）

[4] 高劲松， 陈哨东， 王丕宏. 越肩发射的两种方式[J]. 火力与指挥控制， 1998， 23（4）： 10-13.

Gao Jinsong， Chen Shaodong， Wang Pihong. Two Launch Modes of Over the Shoulder[J]. Fire Control & Command Control， 1998， 23（4）： 10-13.（in Chinese）

[5] Taur D R， Chern J S. An Optimal Composite Guidance Strategy for Dogfight AirtoAir IR Missiles[C] ∥ AIAA Guidance， Navigation， and Control Conference and Exhibit， Portland， Oregon， 2013.

[6] Bugajski D J， Enns D F. Nonlinear Control Law with Application to High AngleofAttack Flight[J]. Journal of Guidance， Control， and Dynamics， 1992， 15（3）： 761-767.

[7] Hirokawa R， Sato K， Manabe S. Autopilot Design for a Missile with ReactionJet Using Coefficient Diagram Method[C] ∥AIAA Guidance， Navigation， and Control Conference and Exhibit， Montreal， Canada， 2001.

[8] 崔彦凯， 王志刚. 越肩发射空空导弹气动力/推力矢量复合控制器设计[J]. 宇航学报， 2010， 31（4）： 1100-1104.

Cui Yankai， Wang Zhigang. Aerodynamic and Thrust Vector Complex Controller Design of Over the Shoulder AirtoAir Missile[J].Journal of Astronautics， 2010， 31（4）： 1100-1104.（in Chinese）

[9] 聶川义， 郭建国， 周军， 等. 空射弹道导弹助推段弹道设计与优化[J]. 飞行力学， 2012， 30（4）： 357-361.

Nie Chuanyi， Guo Jianguo， Zhou Jun， et al. Design and Optimization of Boost Phase Trajectory for AirLaunched Ballistic Missile[J]. Flight Dynamics， 2012， 30（4）： 357-361.（in Chinese）

[10] 鲜勇， 刘炳琪， 王安民， 等. 变射面弹道横向转弯飞行程序的设计与优化[J]. 弹道学报， 2014， 26（4）： 30-35.

Xian Yong， Liu Bingqi， Wang Anmin， et al. Design and Optimization of Lateral Turning Flight Program on Changeable Launching Plane Trajectory[J]. Journal of Ballistics， 2014， 26（4）： 30-35.（in Chinese）

[11] Innocenti M， Thukral A. Simultaneous ReactionJet and Aerodynamic Control of Missile Systems[C] ∥AlAA Guidance， Navigation， and Control Conference， Monterey， California， 1993.

[12] Thukral A， Innocenti M. A Sliding Mode Missile Pitch Autopilot Synthesis for High Angle of Attack Maneuvering[J]. IEEE Transactions on Control Systems Technology， 1998， 6（3）： 359-371.

[13] Huntington G T， Rao A V. Optimal Reconfiguration of Spacecraft Formations Using the Gauss Pseudospectral Method[J]. Journal of Guidance， Control， and Dynamics， 2008， 31（3）： 689-697.

[14] 杨希祥， 张为华. 基于Gauss伪谱法的空空导弹最优中制导律设计[J]. 国防科技大学学报， 2013， 35（1）： 28-35.

Yang Xixiang， Zhang Weihua. Midcourse Guidance Law Optimal Design for AirtoAir Missiles Based on Gauss Pseudospectral Method[J]. Journal of National University of Defense Technology， 2013， 35（1）： 28-35.（in Chinese）