城市轨道交通系统单列车能耗优化
余后伦,熊舒威,郭嫚
(西南交通大学交通运输与物流学院,四川成都 610031)
城市轨道交通系统单列车能耗优化
余后伦,熊舒威,郭嫚
(西南交通大学交通运输与物流学院,四川成都 610031)
低碳环保、节能减排是铁路未来的发展趋势,为减少城市轨道列车的能耗,将列车处理为单质点模型,近似地认为城市轨道列车在两站间只经历牵引、惰行和制动3个阶段,在此基础上建立具有代表性的城市轨道交通系统单列车能耗优化的非线性规划模型,利用序列二次规划法(SQP)优化求解,并给出算例验证其可行性。
城市轨道交通;单质点模型;阶段;能耗;序列二次规划法
低碳环保、节能减排是铁路未来的发展趋势,列车运行过程中的能耗问题愈发引人关注。据统计,轨道交通系统中列车牵引能耗占总能耗的40%以上[1],为了顺应绿色交通的发展趋势,节约能源消耗,列车的节能优化运行成为近年来比较热门的研究话题。对列车运行时的耗能状况加以分析研究,设计出能耗最小的列车开行方案对铁路的未来发展具有重要意义。
1 列车线路运行情况分析
理论条件下,在列车运行图规定的运行时间内,列车可以根据需要合理安排和调整各个阶段的运行时间使列车能耗最小。根据线路状况和列车特性,每条轨道线路都存在一个限制速度,列车运行过程中速度不允许超过轨道线路设计的限制速度。限制速度会周期性更新。列车在线路限制速度条件约束下经历以下几个阶段[2-4]:
1)牵引阶段。列车加速运行,机车发动机做功耗能。
2)巡航阶段。列车匀速,列车所受合外力为0。

图1 列车区间运行工况
3)惰行阶段。列车既不牵引也不制动,列车总阻力决定其速度状态,发动机不耗能。
4)制动阶段。列车在制动力和总阻力共同作用下做减速运动,发动机不做功。
城市轨道交通系统站间距较短,所以列车巡航时间极短,惰行的加速度也较小,巡航阶段完全可以用牵引和惰行代替,列车在两站间的运行可看成只经历牵引、惰行、制动3个阶段。因此,列车的线路运行情况如图1所示[5]。
对整个列车走行过程微元处理并建立目标节能函数和相关约束条件,可得到一个既有等式约束也有不等式约束的非线性规划问题模型,这种小型非线性规划问题可用二次规划算法求最优解[6],得到的列车在城市轨道交通系统中的最优运行时间和运行加速度可以给城市轨道交通系统的决策者提供参考,进一步地使列车运行达到节能减排的目的。
2 建模与求解
2.1 列车受力分析

图2 列车区间运行受力分析
列车运行时的受力状态非常复杂,通常为了简化处理,将列车运行模型视为单质点模型,在牛顿运动学定律的范畴内考虑其受力情况,列车运行过程中受到列车自身重力G、机车牵引力F、列车运行遇到的总阻力W和制动力B的作用[7-8],如图2所示。
1)列车单位牵引力F
F=μff,
式中:μf为列车牵引系数;f为列车最大单位牵引力,N/kN。
2)列车运行单位总阻力W
根据列车阻力形成的原因不同,分为基本阻力和附加阻力[9-10]
①单位基本阻力
r=A+Bv+Cv2,
式中:r为单位基本阻力,N/kN;A、B、C为阻力多项式系数,通常取经验值;v为列车运行速度,km/h。
②单位附加阻力
w=wi+wc,
式中:w为单位附加阻力,N/kN ;wi为单位坡道附加阻力,N/kN;wc为单位曲线附加阻力,N/kN。
③单位总阻力
W=r+w,
3)列车单位制动力B
B=μbb,
式中:μb为列车制动系数;b为最大单位制动力,N/kN。
2.2 建模
优化目标是使列车在车站之间运行时能耗最少。假设列车在整个走行过程中质量保持不变;由于城市轨道系统中车站间距离较短,列车在两站间运行只经历牵引—惰行—制动3个阶段且不会在其中两个阶段循环;列车运行时只考虑外力的影响[11-14]。
假设两站间的距离为L,3个阶段的列车运行距离为si(i=1,2,3),运行时间为ti(i=1,2,3),每个阶段结束进入下一个阶段的列车速度为vi(i=0,1,2,3),每个阶段的限制速度为vl(l=1,2,3),每个阶段的加速度为ai(i=1,2,3)。
根据列车受力分析,得
式中g为重力加速度,g=9.8 m/s2。有
根据动力学原理有
式中:E为列车运行能耗;ΔEi为第i个阶段的耗能。
列车在两站间按列车运行图规定的时间T内走行时,有
时间约束
距离约束
速度约束
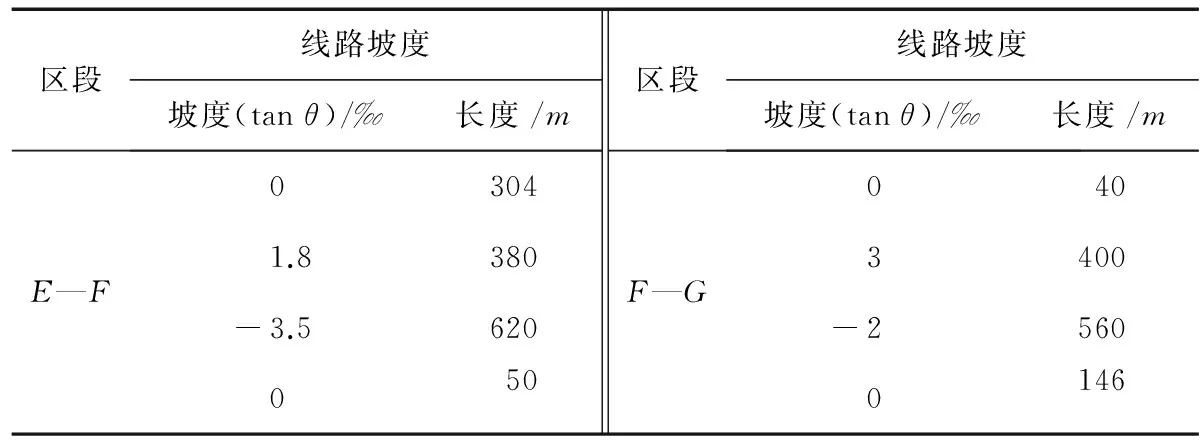
vi 对于牵引阶段,运行的时间t1和距离s1为[15]: 对于惰行阶段,运行的时间t2和距离s2为: 对于制动阶段,运行的时间t3和距离s3为[16]: 根据优化的目标和约束,可得到列车的能耗优化模型[17]: s.t. vi 0<μf<1, 0<μb<1, v0=v3=0, ti>0, si>0。 2.3 求解 上述优化模型的约束条件中除了有等式约束外还有不等式约束,所以此能耗优化模型是一个典型的非线性规划问题。序列二次规划法(SQP)可求解这类中小型非线性规划问题。 在模型中,vi和ti用向量表示,Ck(x)表示约束函数,将m记为模型中约束条件的总数,me记为等式约束条件的个数,则不等式条件约束的个数为m-me[18]。 将原规划问题改写成: s.t. Cn(x)=0,n=(1,2,…,me) (1) 然后构建拉格朗日函数 SQP算法计算步骤如下: 1)将非线性约束条件线性化可以将此规划问题转化为二次线性规划问题 s.t. 式中:d为变量搜索方向;Bk为拉格朗日函数的Hessian矩阵的正定拟牛顿条件。 2)求解二次线性规划子问题得到一个搜索方向dk,然后可通过线性搜索得到步长αk。 3)得出一组决策变量 xk+1=xk+αkdk。 (2) 4)通过式(2)更新Hessian矩阵 5)计算式(2),若结果满足式(1)且目标函数的值不再下降,则结束,所得的解即是满足条件的最优解。若不满足或目标函数的值仍出现下降,则返回至2)继续按上述步骤进行计算,直至结果满足式(1)且目标函数的值不再下降。 本模型是一个典型的迭代计算的优化问题,用Lingo软件来进行求解。 3.1 实际问题 表1 车站之间线路情况 某市地铁线路中3个车站之间线路坡度情况如表1所示。在E—F段,限速55 km/h的路段120 m,限速80 km/h的路段1 234 m。在F—G段,限速55 km/h的路段为306 m,限速80 km/h的路段为840 m。μi、μb的取值如表2所示[19-20]。 表2 列车牵引制动系数 列车参数如表3所示。 表3 列车参数 列车牵引和制动特性曲线表示为: 3.2 求解 列车从E站出发到达G站,E站和G站间总运行时间规定为220 s(不包括停站时间),利用Lingo软件可求得优化后(最节能运行的速度距离曲线)的各阶段的运行时间如表4所示。 表4 列车最优运行时间和加速度 利用Matlab软件进行仿真可得列车在两区间的最优运行曲线如图3所示。 利用Lingo优化软件计算得出最优化区间运行总能耗为9.077 1 kW·h。 图3 列车在两区间的最优运行曲线 针对单列车运行的牵引、巡航、惰行、制动4个阶段的运行特点,结合城市轨道交通系统站间距较短的特征,近似地认为列车在城市轨道交通系统中相邻两站间运行时只经历牵引、惰行和制动3个阶段,在动力学模型和多目标优化的基础上,建立相应的列车能耗优化模型,此模型的约束条件中包含有等式约束和不等式约束。采用序列二次规划法(SQP)优化求解小型的非线性规划问题模型,优化结果可以给相关的城市轨道交通部门制定更合理的节能开行方案提供参考。 此外,对列车进行动力学分析是以单质点的形式处理的,这种单质点的处理不能很好地应对列车在变曲率线路和变坡道线路复杂的外力渐变情况,因此列车运行优化过程中不能最准确地体现其运动状态从而影响结果准确性,所以在研究城市轨道交通系统中列车运行能耗相关的问题时应多展开对列车的多质点动力学模型研究。 [1]顾青.城市轨道交通列车节能优化驾驶研究[D].北京:北京交通大学,2014. GU Qing. Energy-efficient optimization driving method for trains in urban rail transit[D].Beijing:Beijing Jiaotong University,2014. [2]胡鹏.城市轨道交通列车运行能耗优化及仿真[D].成都:西南交通大学,2013. HU Peng.Train operation energy optimization and simulation in urban rail transit system[D].Chengdu:Southwest Jiaotong University,2013. [3]宋琦,顾青,刘峰,等.高速列车的自适应速度及位置控制[J].控制工程,2010,17(S1):35-37. SONG Qi,GU Qing,LIU Feng,et al.Adaptive positioning and velocity control of high speed train systems[J].Control Engineering,2010,17(S1):35-37. [4]罗恒钰,徐洪泽.基于参考模型的ATO自适应控制算法研究[J].铁道学报,2013,35(7):68-73. LUO Hengyu, XU Hongze. Study on model reference adaptive control of ATO systems[J].Journal of the China Railway Society,2013,35(7):68-73. [5]RUELLAND Francois,AL-HADDAD Kamal.Reducing subway′s energy[C].Proceedings of 2007 IEEE Canada Electrical Power Conference.Canada:IEEE Press,2007:261-267. [6]杨光.城市轨道列车牵引计算仿真系统的设计与实现[D].兰州:兰州交通大学,2013. YANG Guang.Design and implementation of the traction calculation simulation system for the urban rail train[D].Lanzhou:Lanzhou Jiaotong University,2013. [7]张翼.牵引策略对动车组能耗的影响研究[D].长沙:中南大学,2014. ZHANG Yi.Research on the impact of traction strategy for energy consumption of the CRH[D].Changsha:Central South University,2014. [8]朱晓敏,徐振华.基于单质点模型的城市轨道交通列车动力学仿真[J].铁道学报,2011,33(6):14-19. ZHU Xiaomin,XU Zhenhua.Dynamic simulation of urban rail transit train based on single-particle model[J].Journal of the China Railway Society,2011,33(6):14-19. [9]石国春.关于序列二次规划(SQP)算法求解非线性规划问题的研究[D].兰州:兰州大学,2009. SHI Guochun.Research on algorithm of seqential quadratic programming for nonlinear programming problems[D].Lanzhou:Lanzhou University,2009. [10]樊莹莹.一种列车运行控制优化方法研究[D].北京:北京交通大学,2013. FAN Yingying. Research on train operation control optimization algorithm[D].Beijing:Beijing Jiaotong University,2013. [11]杨文.基于无模型自适应控制的列车节能优化运行方法研究[D].北京:北京交通大学,2013. YANG Wen. The study on energy efficient operation strategy for trains based on model-free adaptive control[D]. Beijing:Beijing Jiaotong University,2013. [12]付印平.列车追踪运行与节能优化建模及模拟研究[D].北京:北京交通大学,2009. FU Yinping.Research on modeling and simulations of train traeking operation and saving energy optimization[D]. Beijing:Beijing Jiaotong University,2009. [13]于雪松.城市轨道交通列车节能优化及能耗评估[D].北京:北京交通大学,2012. YU Xuesong. Train behavior optimization of urban rail transit system considering energy saving[D].Beijing:Beijing Jiaotong University,2012. [14]马超云,丁勇,杜鹏,等.基于遗传算法的列车节能运行惰行控制研究[J].铁路计算机应用, 2010,19(6):4-8. MA Chaoyun, DING Yong, DU Peng,et al. Study on coast control of train movement for saving energy based-on genetic algorithm[J].Railway Computer Application,2010,19(6):4-8. [15]丁勇,刘海东.地铁列车节能运行的两阶段优化模型算法研宄[J].交通运输系统工程与信息,2011,11(1):96-101. DING Yong, LIU Haidong.A two-level optimization model and algorithm for energy-efficient urban train operation[J].Journal of Transportation Systems Engineering and information Technology,2011,11(1):96-101. [16]荀径.基于智能体和元胞自动机的列车协同控制研究[D].北京:北京交通大学,2011. XUN Jing. Research on coordinated train control by using agent and cellular automata[D].Beijing:Beijing Jiaotong University,2011. [17]文孝霞,杜子学,杨林.基于遗传算法的跨坐式单轨列车牵引曲线优化研究[J].铁道机车车辆,2011,31(4): 83-87. WEN Xiaoxia, DU Zixue, YANG Lin. Traction curve optimization of straddle-type monorail train based on genetic algorithm[J].Railway Locomotive & Car,2011,31(4):83-87. [18]陈荣武,郭进.基于遗传算法的列车能耗优化与仿真[J].交通运输工程学报,2012,12(1):108-114. CHEN Rongwu, GUO Jin.Optimization algorithm of train operation energy consumption based on genetic algorithm[J].Journal of Traffic and Transportation Engineering,2012,12(1):108-114. [19]ALBRECHT T.Reducing power peaks and energy consumption in rail transit systems by simultaneous train running time control[J].WIT Transactions on State of the Art in Science and Engineering, 2010,39:3-12. [20]LI K P, GAO Z Y, NING B. Modeling the railway traffic using cellular automata model[J].International Journal of Modem Physics C, 2005,16(6): 921-932. (责任编辑:郭守真) Energy Consumption Optimization of Single Train in Urban Rail Transit System YUHoulun,XIONGShuwei,GUOMan (Schooloftransportationandlogistics,SouthwestJiaotongUniversity,Chengdu610031) The low-carbon environmental protection and energy-saving emission reduction are the future development trend of railway. To optimize the energy-saving operation of the train, the train is treated as a single particle model and approximately considered as only running the three stages of traction, coasting and braking. On this basis, this paper establishes a typical non-linear programming model for optimizing the energy consumption of single train in the urban rail transit system, uses the sequence quadratic programming (SQP) algorithm to calculate the optimization and gives an example to verify its feasibility. urban rail transit system; single-particle model; stage; energy consumption; sequence quadratic programming algorithm 2016-08-03 国家自然基金项目(61273242,61403317,60776826);中国铁路总公司科技研究计划项目(2015X008-B, 2016X006-D);四川省科技厅软科学计划项目(2015ZR0141);中央高校基本科研业务费专项资金资助(2682015CX043) 余后伦(1992—),男,湖北鄂州人,硕士研究生,主要研究方向为运输组织优化,E-mail:156586712@qq.com. 10.3969/j.issn.1672-0032.2017.01.003 U268.6 A 1672-0032(2017)01-0014-07
Cn(x)<0,n=(me+1,…,m)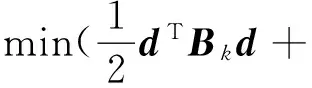



3 单列车能耗优化实例




4 结语

