A Distributed User Association and Resource Allocation Method in Cache-Enabled Small Cell Networks

Gongye Ren, Hua Qu, Jihong Zhao,2, Shuyuan Zhao, Zhirong Luan School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 70054, China

2 School of Telecommunication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710061, China

I. INTRODUCTION

The past ten years witness a 4000-fold growth in mobile data traffic with the proliferation of smart phones, portable tablets and abundant wireless services. In particular, mobile video traffic accounted for 55 percent of total mobile data traffic in 2015, and three-fourths of the world’s mobile data traffic will be video by 2020 [1]. To satisfy these strong demands,wireless communication technologies have evolved from traditional GSM systems to current LTE-A systems, and they are oriented toward 5G networks now. The spectrum efficiency has experienced substantial promotion due to advanced air interface technologies, e.g.OFDM, massive MIMO, soft frequency reuse and so on. Small cell networks [2][3] and additional spectrum allocation [4] have also been introduced to further enhance network capacity. On one hand, these regular methods either are approaching their limits, or confront exorbitant costs, and they can’t keep up with the rate of traffic growth [5]. On the other hand, these methods only focus on data rates at physical layer, and dismiss the contents

In this paper, a distributed relaxing-rounding method is proposed for user association and resource allocation in cache-enabled small cell networks.contained in the bit streams. Therefore, innovative content-centric networking paradigms are needed to handle this challenge.

With the boom of social networks and video-on-demand services, the data traffic in cellular networks has shown significant regularities [6][7]. Particularly, asynchronous content reuse is a remarkable characteristic among them during the content delivery in wireless networks [8]. Lots of resources are occupied to transmit the same contents to different users at different time, which decreases the spectrum efficiency and energy efficiency. In view of this, Molisch et al. propose a new network architecture in which contents are cached in femto base stations and users’ terminals [5][9]. In [10], a proactive networking paradigm is introduced, in which the users’ demand profiles can be learnt from massive context information, historical service information and social relationships among users. [11] discusses potential techniques for caching in 5G mobile networks, including not only radio access network caching but also evolved packet core network caching. Users in these cache-enabled wireless networks can obtain most contents directly from local storage, nearby devices and small base stations (SBSs), which immensely improves spectrum efficiency and energy efficiency.

Generally, there are two issues to be addressed for realizing this proactive caching paradigm [12]. On one hand, a content placement scheme determining which contents are cached at each BS and/or terminal is critical to the benefits of proactive caching. These problems are often modeled as integer programming problems and simple user association schemes are assumed. [13] proposes approximation algorithms for resolving this NP-hard wireless distributed caching problem which aims at minimizing the average delay for all users. [14] formulates the cache allocation policy as a convex optimization problem and solves it in a distributed manner using the alternating direction method of multipliers approach. [15] gives an optimal probabilistic content placement policy to maximize the overall user’s hit probability based on stochastic model. A content replacement mechanism based on multi-object auctions is proposed in[16] for dealing with the competition among service providers.

On the other hand, content delivery schemes direct how to deliver contents to users (e.g., routing, resource allocation mechanisms) under given caching situations. [17]proposes a user association scheme based on one-to-many game, which aims at minimizing the total backhaul usage. In [18], a joint routing and caching problem is reformulated as facility location problem, which is targeted at maximizing the fraction of content requests served locally by SBSs. Similarly, [19] jointly optimizes user association and content placement for maximizing the weighted sum of network utility and backhaul saving. Taking device-to-device (D2D) communications into account, the authors of [20] jointly optimize user association, resource allocation and content refreshment.

In effect, minimizing the backhaul usage makes the backhaul links idle in a fraction of each time slot and it restricts the transmission of some contents that must be retrieved via backhaul links. In addition, since the different time scales of content placement and content delivery, aforementioned joint optimization schemes are difficult to implement in practice.In view of these, in this paper, we only focus on the joint optimization of user association[21] and resource allocation in a cache-enabled small cell network under given content placement situation. The contents are stored in the caches of SBSs in advance. Users are associated with macro base stations (MBSs)or SBSs and allocated appropriate resources according to the proposed method. The joint optimization problem of user association and resource allocation is formulated as a MINLP problem. Unlike the general approaches,we maximize the weighted sum of the total utility of data rates and the total data rates retrieved from caches, and backhaul capacity is fully utilized. A distributed relaxing-rounding (DRR) method is proposed to solve this problem, which comprises three steps. Firstly,we solve the relaxed convex problem by a distributed algorithm, whose solution signifies fractional association. Then we round the fractional association solution to single association solution. Finally, this single association solution is brought into original MINLP problem and the optimal resource allocation scheme under this single association solution is derived by the former distributed algorithm again. Simulation results show that the solution of the DRR method approximates well to the optimal solution of the MINLP problem in practical scenarios.

The rest of this paper is organized as follows: system model is described in Section II. Section III formulates the optimization problem and Section IV presents the proposed DRR method as well as implementation details. Section V gives the numerical results and finally, conclusions are drawn in Section VI.

Notation: Column vectors and matrices are denoted by lower case and upper case boldface letters, respectively. All the norms in the paper are Euclidean norms, and finally,x+=max{0,x} .

II. SYSTEM MODEL

We consider the downlink scenario of a heterogeneous cellular network composed of a MBS and multiple SBSs. Let M and N denote the set of all BSs and all users, respectively. Correspondingly, M and N are the total number of BSs and users, respectively.All BSs adopt co-channel deployment and users are served by time division multiple access(TDMA) mechanism. For BS i, its transmit power is Piand it is connected to the core network via a backhaul link with capacity Ci. We assume all the SBSs have identical backhaul capacity CSBS. Since a large portion of SBSs(e.g., femtocells) are deployed by subscribers with limited backhaul links such as digital subscriber line (DSL) or cable modem [22],their backhaul capacities are much smaller than those of MBSs. Each SBS is equipped with a data storage unit with equal capacity S (with the unit of the number of files it can store) for storing strategic contents and in contrast, MBS has no cache.

During a certain period, the set of all files possibly requested by users is denoted by F,which contains F files in it. We assume all files have the same sizes. For the case that contents have different sizes, they can be divided into blocks with equal sizes or by leveraging advanced coding techniques [18]. At the beginning of this period, certain content placement strategy has been executed, and some contents have been cached at each SBS.The cached contents on BS i is denoted by fi∈{0,1}F, where the f-th element is 1 means BS i caches the f-th contents, otherwise it doesn’t cache. Note that we have 1Tf≤S if

Fi

i denotes a SBS (1Fdenotes a F-dimensional column vector that all the elements are 1).In the sequel, we use contents and files interchangeably.

At a certain moment in this period, N users request contents from F in the network. We assume that a user can only request one file at a time. The requested content of user j is denoted by qj∈{0,1}F, and there is only one element 1 in qjwhose index represents the requested content. When user j is associated with BS i, the maximum achievable transmit rate cijcan be calculated by the following Shannon formula:

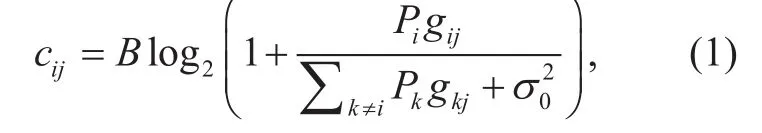
where gijdenotes the flat channel gain between BS i and user j, σ02denotes noise power level and B denotes bandwidth. We focus on a snapshot model with static users during the call holding time (a few minutes).Thus, gijonly includes path loss and shadowing, and the fast fading is not considered here because the time scale of measuring channel gain (over the lifetime of a content transmission) is much larger than the coherence time of a wireless channel. In addition, we assume a user can attach to only one BS at a time. When user j connects to BS i, if=1, namely the requested content of user j is cached at BS i, this content can be transmitted directly from BS i without occupying backhaul link.Otherwise the content must be retrieved from remote server.

III. PROBLEM FORMULATION

which denote the total utility of data rates and the total data rates retrieved from caches,respectively. For achieving fairness among users, logarithmic utility function is applied. xijis a binary variable indicating user association.xij=1 means user j is associated with BS i and xij=0 otherwise. pijis a continuous variable denoting the fraction of resource that BS i allocates to user j. The total resource of the BS is normalized to 1.andis the weight of f1(P)and u1, u2are normalization factors for these two components, respectively. Denote the optimal points of f1(P) and f2(P), subject to the same constraints as (2), by P[1]and P[2],respectively, then u1and u2can be determined by the following formulas [23]:

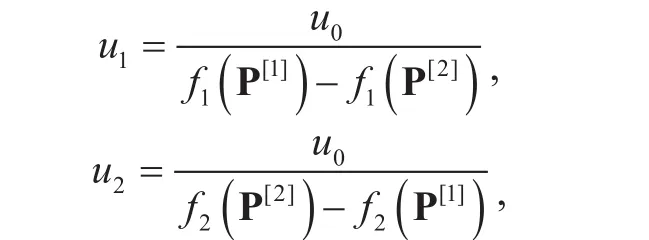
where u0is a constant for amplifying the value of f(P) to normal range.

The objective function of (2) makes a trade-off between the total utility of data rates and the total data rates retrieved from caches.In contrast to most mathematical models in caching scenarios, the backhaul capacity is fully utilized for enhancing users’ experience,as indicated by C1 of (2). C2-C5 are essential constraints for user association and resource allocation problems in single association scenario.

The problem (2) is a MINLP problem,which is NP-hard [24]. If the integer constraints are replaced by xij∈[0,1], fortunately it is convex. The following section presents our approach for solving it.

IV. DISTRIBUTED RELAXING-ROUNDING METHOD

Firstly, we relax the binary constraints xij∈{0,1} to the range constraints xij∈[0,1].Then a distributed algorithm is proposed to solve the relaxed problem. After obtaining the relaxed solution, we adopt a rounding method to get the binary values of xij, and bring them back to (2). A simplified version of (2) is got and it can be resolved by the same distributed algorithm as before. For convenience, we refer to our proposed approach as DRR method.

4.1 Double dual decompositions

In this subsection, we apply dual decomposition method twice to solve the relaxed version of (2). After been relaxed, problem (2) can be rewritten as:

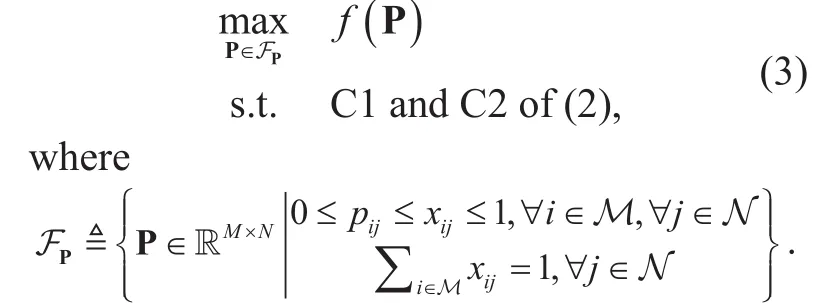
Since all the constraints of (3) are affine,and the feasible set is nonempty, (3) satisfies Slater’s condition for convex optimization problems and strong duality holds [25]. Therefore, we can solve the primal problem by solving its dual problem. Notably, problem (3) is a kind of network utility maximization problems[26], and inherent separable structure can be leveraged to design distributed algorithms.

As we can see, for given λ and υ, evaluating g(λυ,) can be conducted at individual users, which forms a distributed algorithm.Since the objective function of (5) is not a strictly concave function of xj, thus g(λυ,)is nondifferentiable [27]. Note that g(λυ,) is a convex function, we adopt projected subgradient method to minimize it, and λ and υ are updated as follows [28]:

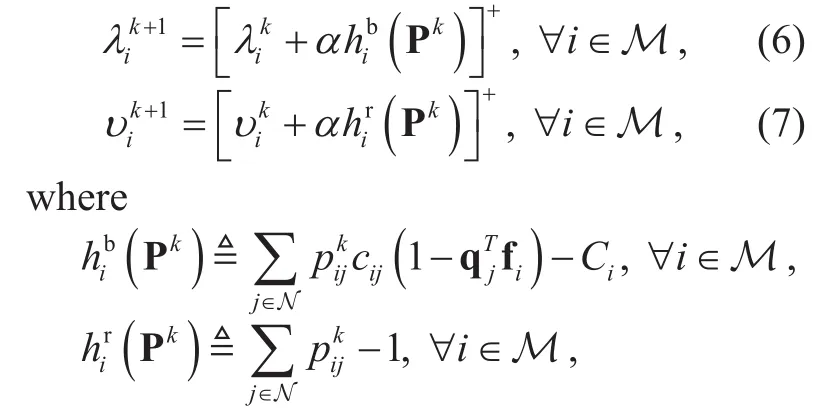
and they are negative subderivatives of g(λ,υ) with respect to λiand υi, respectively [27]. Pkdenotes the collection of the optimal points of (5) for j=1,2,…,N under given λkand υkat the k-th iteration. α is a small positive stepsize.

For given μj, (9) can be easily solved by gradient projection method, and (10) is solved by assigning, and xi′j=0 otherwise. If there are more than one maximum, choose any one of the corresponding xijto be 1. Unlike the first dual decomposition, the dual method for solving (5)is totally executed in each user’s device.

As problem (4), gj(λ,υ,μj) is nondifferentiable with respect to μj, projected subgrandient method is employed again to solve (8).The update rule of μjis:

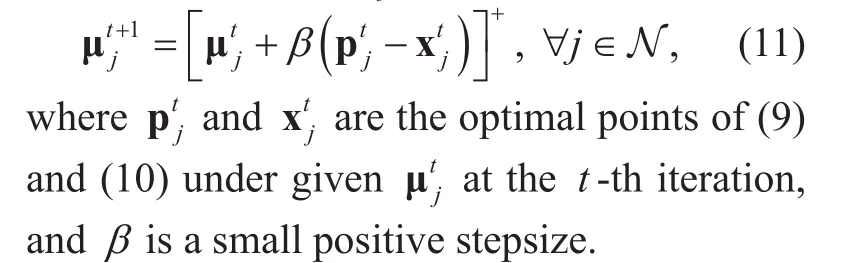
In a word, at first, the dual decomposition method is applied to solve master problem (3),which generates a distributed algorithm. This operation is called master decomposition. For getting the dual functions in each iteration of master decomposition efficiently, dual decomposition method is used again, and we name it secondary decomposition. According to Proposition 3 in [29], with proper stepsizes α and β, and large enough number of iterations, the average of all the outputs up to the k-th iteration, i.e.,, will converge to the optimal solution of the relaxed problem(3).

Remark 1(intuitive interpretation). In the master decomposition, λ and υ bear significant messages about the backhaul usages and resource usages of all BSs. Specifically, they can be regarded as the “price” to utilize the backhauls and resources of all BSs. We expand on this for λ, and υ possesses similar interpretation. For BS i, we assume＞0. If＜0, which means that BS i has spare backhaul capacity, then we haveaccording to (6). For user j, ifmeans the requested file of user j must be retrieved via backhaul of BS i), the reduction ofincrease, which promptsto move towards 1. This means that user j tendslto connect to BS i to utilize its residual backhaul capacity for improving overall objective.Otherwise, ifwill increase.For user j withmoves to 0,which brings about that user j departs from BS i for alleviating backhaul congestion.

Algorithm 2 The procedures at BS i

4.2 Algorithms

For clarity, first of all, the master decomposition presented in 4.1 for solving (3) is summarized in Algorithm 1 and Algorithm 2, which conduct at user’s side and BS’s side, respectively. The secondary decomposition procedures are omitted in Algorithm 1 for brevity.

Remark 2(complexity). At each iteration of the distributed algorithm, the computation complexity of the algorithm at user’s side is O(M) and that at BS’s side is O(N). As to the centralized algorithm, the computation complexity is O(MN) at each iteration. The amount of exchanged information in distributed algorithm is MN from users to BSs,and 2M from BSs to users at each iteration.While that is proportional to MN for centralized method. Thus, the distributed algorithms are suitable for large scale systems where the central controllers have limited computation capability, although it may bring out extensive information exchange.

After obtaining the optimal point of the relaxed problem (3), denoted by P∗, in order to derive the single association scheme,we direct user j to connect to the BS i′ ifThis operation is referred to as rounding process. When there are more than one maximum, any one of them is chosen. Thus, another problem similar to (2)is derived, in which variables {xij} disappear.This problem can also be solved by the distributed algorithm as above. Because there is one and only one non-zero element in pj, the problems similar to (5) can be easily solved by users’ devices. This process is omitted for limited space.

Thus, the complete DRR method is composed of three steps: 1) Solve the relaxed problem (3) by the proposed distributed algo-rithm and derive P∗; 2) Round P∗and derive the single association solution; 3) Bring this solution into (2) and the consequential problem is solved by the distributed algorithm again. We refer to step 1 and step 3 as user association (UA) phase and resource allocation(RA) phase hereinafter, respectively. Simulation results in section V demonstrate the optimal value generated by the DRR method is near the theoretical upper bound of the optimal value of (2), which means the solution of DRR method approximates the optimal solution of(2).

4.3 Implementation

The proposed DRR method complies with the specifications of the dominant LTE-A systems and it can be easily implemented in current networks. Specifically, the transmissions of qj, pjand {cij} from user j to all BSs can be done via the Physical Uplink Control Channel (PUCCH) and X2 interfaces, and fi,of BS i can be broadcast to all users via Physical Broadcast Control Channel(PBCH). In addition, {cij} can be calculated according to pilot signals [30].

This work focuses on general content demands of users, and doesn’t distinguish between video streaming and file download. In this framework, for video streaming services,high quality videos are cached at BSs at first.When users request these videos, if the wireless link capacity can support these high quality videos (the offered data rates are larger than the video playback rates), they will be transmitted without transformation. Otherwise, a recoding operation (e.g., scalable video coding[31]) is implemented and the video playback rates are reduced to accommodate to link capacity.

V. NUMERICAL RESULTS AND DISCUSSIONS

In this section, we evaluate the performance of the DRR method in a square area with length 500m, where a MBS is located at the center and 10 SBSs are randomly and uniformly deployed near the cell edges. Detailed simulation parameters are shown in table 1.The default spectrum bandwidth of channel is 10MHz, and the noise power spectral density is -174dBm/Hz. Log-normal shadowing with standard deviation of 8dB is considered in the radio propagation models for both MBS and SBS. The file library F, unless otherwise specified, consists of F=1000 files, and the file popularity distribution follows Zipf distribution [32], i.e., the k-th most popular file is requested with probabilityz is the skew parameter and we set z=0.8 unless otherwise specified. At the beginning of each period (e.g., one hour), some files are pre-downloaded to the cache of each SBS according to the estimated file popularity distribution independently, i.e., the more popular file will be cached at SBSs with higher probability, until reaching the cache capacity. The process constitutes content placement, and we assume that the estimation of file popularity is precise. Note that it is almost impossible for the sets of cached files at two arbitrary SBSs to be identical. There are 100 users randomly and uniformly distributed in this region, and each user requests a file according to file popularity distribution independently.

To demonstrate the performance of the DRR method, we compare it with another four methods: centralized relaxing (CR) method,centralized relaxing-rounding (CRR) method,max-SINR association and range expansion(RE) association. CR method solves the relaxed form of (2) in centralized manner. It results in fractional association and provides the upper bound of optimal value of (2). CRR method rounds the solution of CR and solves the resultant problem by centralized method again. As ordinary association schemes, max-SINR association and RE association don’t take the requested files of users, the cached files of BSs, and the backhaul capacities of SBSs into account. For comparison, in the last two schemes, we assume that resource is equally allocated among the users connecting to the same BSs. If the backhaul links can’t afford the total throughput in some BSs, the allocated resource for each user scales down properly for satisfying backhaul constraints. In RE scheme, we choose 10dB as the offset for SBSs in the following simulation.

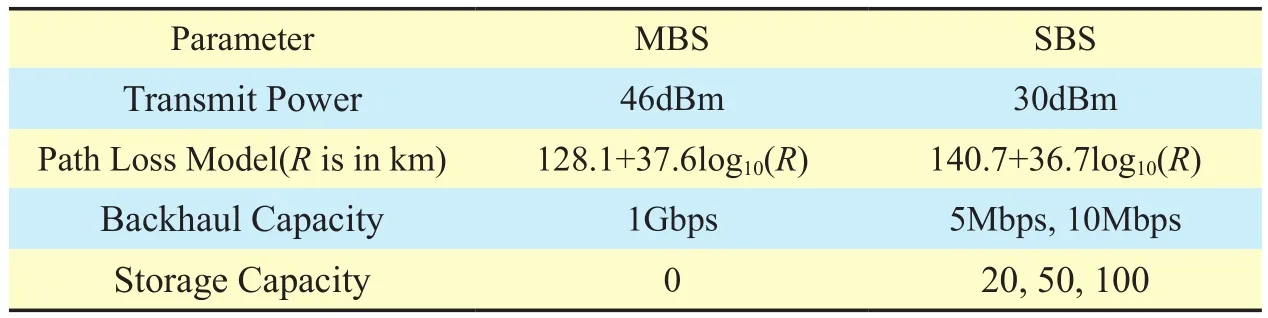
Table I Simulation parameters

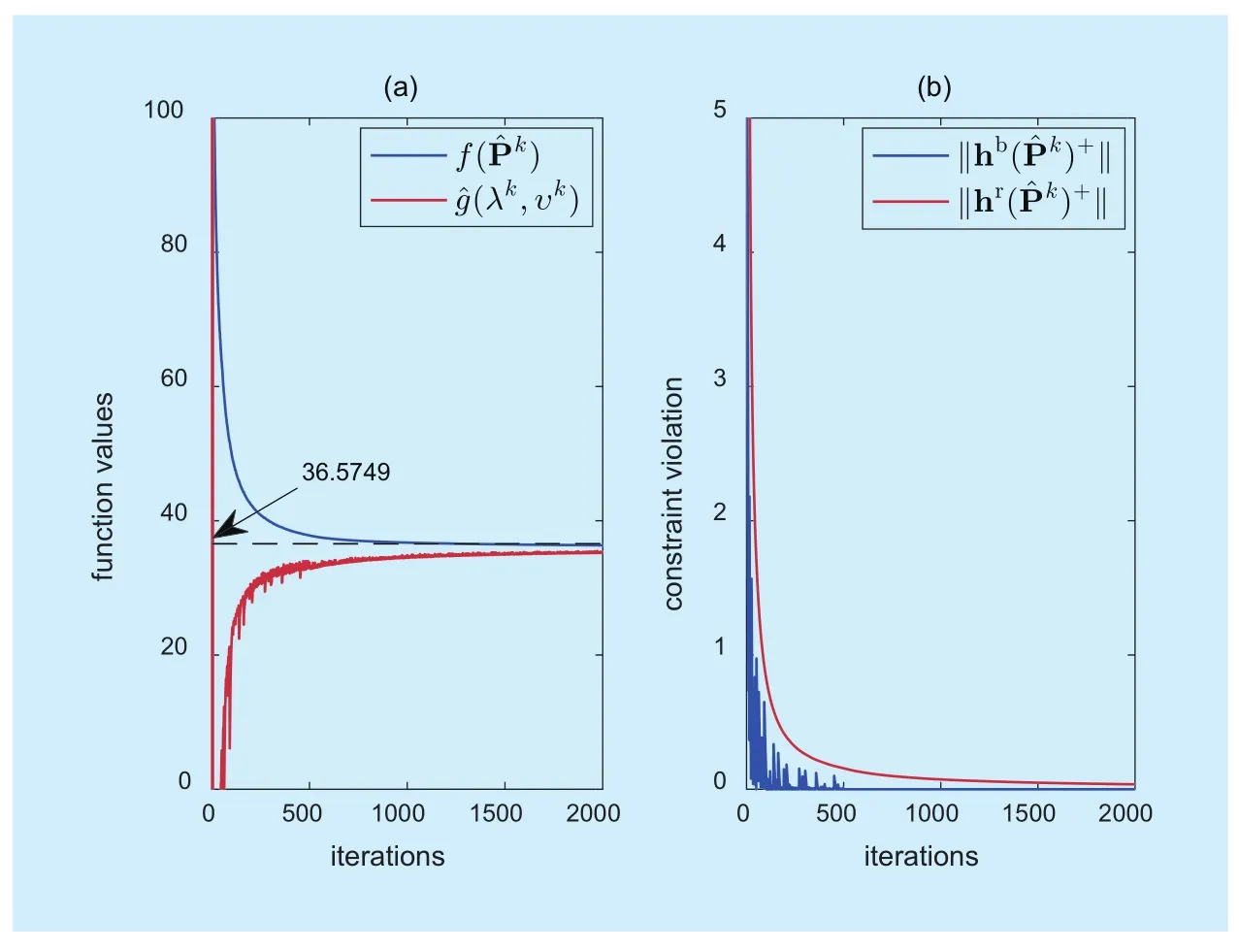
Fig. 1 The convergence results of the dual method in a single network realization.(a) presents the variations of the values of primal objective function and dual objective function and (b) presents the violations of backhaul constraints and resource constraints. A simple dynamic stepsize rule is applied: α=0.4 for the first 100 iterations, α=0.3 for the next 400 iterations, and α=0.2 for the last 1500 iterations. S=50, CSBS=5Mbps and ω=0.8. The vertical axis in each subfigure is restricted in proper range for observation

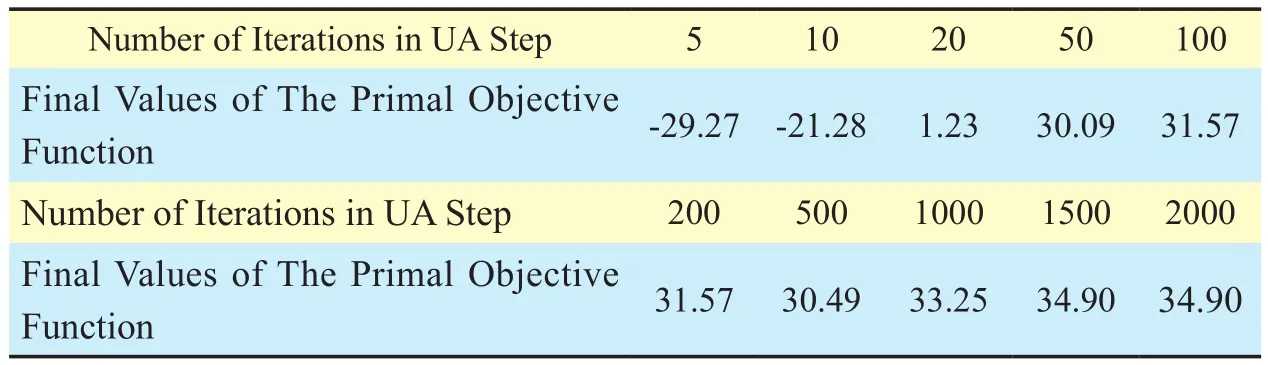
Table II Final values of the primal objective function after RA step

5.1 Convergence properties of the dual method

Firstly, we verify the convergence properties of the dual method for problem (3) in the UA step. Solving the subproblem (5) is conducted in a centralized manner for simplicity. Figure 1(a) shows the variations of the values of primal objective function and dual objective function as the number of iterations grows.Note thatmeans that the dual objective function is also calculated based on

Figure 1(b) presents the evolutions of the violations of backhaul and resource constraints as k increases. As we can see, the dual method yields fairly favorable outcomes when k rises to 1000. Since these two sets of constraints are all inequality constraints, projected subgradient method must be applied to update λ and υ, which results in relatively slow convergence rate compared with the results in [33]. With suitable dynamic stepsize rules[34], the convergence rate can be improved further for practical implementation.

Table 2 provides the final values of the primal objective function after RA step when the UA step terminates at different iterations,which are derived from the same realization in figure 1. When we round Pˆ50(i.e., the UA step terminates at the fiftieth iteration), the final value of the primal objective function after RA step, 30.09, approximates well to the upper bound 36.5749, which is shown in figure 1(a). Hence, the number of iterations in UA step can be lowered for obtaining the solution faster at the expense of tolerable performance degeneration.

5.2 Rate CDF

Figure 2 shows the cumulative distribution functions (CDFs) of the DRR method and other methods. As we can see, the proposed DRR method yields almost identical data rate distribution as CRR and CR method. In max-SINR method, users generally experience lower data rates comparing with DRR scheme. In addition, the data rate distribution generated by RE method is comparable with that of DRR in the range where data rates are larger than 0.7Mbps, but it effects more users with lower data rates, which is unfavorable from the perspective of fairness among users.

5.3 Effects of storage and backhaul capacities

Figure 3 presents the effects of S and CSBSon different methods. On the whole, the proposed DRR method performs better than max-SINR and RE under fi ve configurations except when S=20 and CSBS=10. In addition, we can make the following remarkable observations from this figure.

1) In the DRR, CRR and CR method, when S is small (e.g., S=20), increasing CSBScan improve both f1(P) and f2(P). If S is large(e.g., S=100), however, increasing CSBScan only improve f1(P) and f2(P) will decrease.In the former case, because of the limited cache capacity, the files that don’t be stored in a SBS are probably stored in nearby SBSs. A lot of users will be reassigned to different BSs and reallocated some resources for increasing f1(P) and f2(P) simultaneously when CSBSrises. By contrast, in the latter case, in view of the considerable storage space and the skewness of users’ requests, two points can be concluded: a) If the requested file of a user can be found in the storage unit of a SBS near him/her, it is probably stored at other SBSs in the vicinity; b) If the requested file of a user is not cached in a SBS near him/her, accordingly, it is not probably stored at other nearby SBSs as well. Thus, generally, for a user connecting to the BS that don’t store his/her requested file in low backhaul capacity case, associating him/her with the SBS with the requested file (often far from the user) will enormously reduce user’s data rate (due to large path loss) when CSBSincreases. For maximizing the overall objective, when CSBSincreases, the requested files of some users will be fetched via backhaul links, which results in increased f1(P)and reduced f2(P).

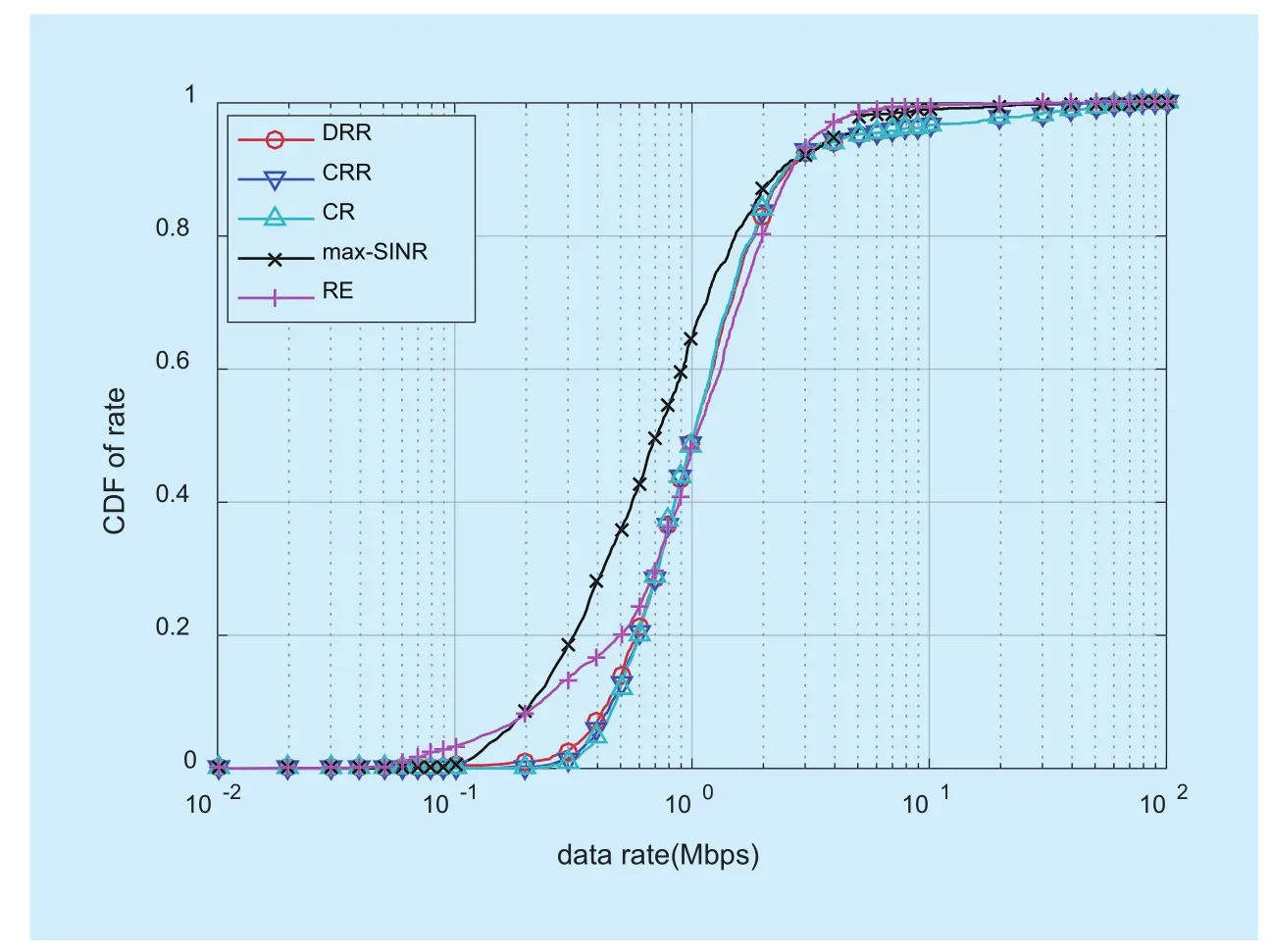
Fig. 2 The CDF of data rates of different methods. S=50, CSBS=5Mbps, ω=0.8

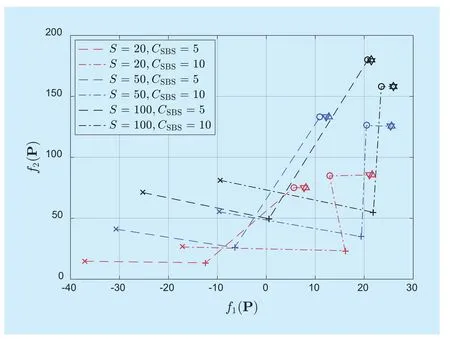
Fig. 3 The values of f1(P) and f2(P) of different methods under different configurations. “×”, “ ＋ ”, “ ○ ”, “ ▽ ” and “ △ ” denote max-SINR, RE, DRR, CRR and CR, respectively. The data points with identical shapes belong to one method and the data points on the same polyline share the same configuration. ω=0.8

2) In all the fi ve methods, with fi xed CSBS,raising S can increase both f1(P) and f2(P).Intuitively, raising S enhances the probability that requested files are cached (i.e. hit probability), which spares much backhaul capacity for other non-cached traffic. Therefore, f1(P)and f2(P) will increase simultaneously.

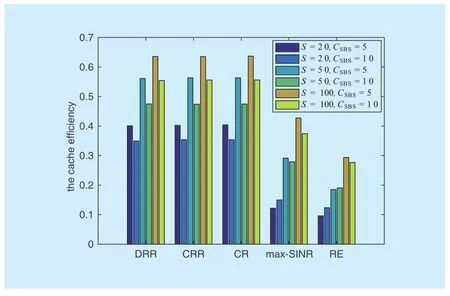
Fig. 4 The cache efficiency of different methods under different configuration.ω=0.8

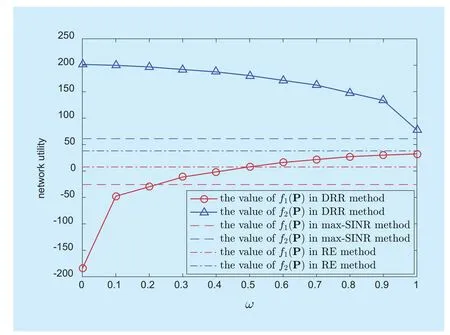
Fig. 5 The effects of weight on the values of f1(P) and f2(P) in a single network realization. S=50, CSBS=5Mbps

3) The performance of the DRR method approaches that of the CRR method as S becomes larger and CSBSbecomes smaller. This results from the characteristic of the projected subgradient method. When S is large and CSBSis small, the absolute value of subderivative of g(λ,υ) with respect towill be small, which prompts that λ accurately approach to the optimal dual variable λ∗(refer to (6)). Thus the averaged Pˆkwill converge to the optimal solution P∗of (3) as k increases and the rounded results are close to those of centralized method. In addition, when S is large and CSBSis small, the optimal value of the DRR method approximates well to that of the CR method, which is the upper bound of the optimal value of (2). In other words, the solution of the DRR method approximates the optimal solution of (2) in this case. Due to the low price of storage units and the high cost of backhaul links, SBSs are often equipped with high-capacity storage units and low-capacity backhaul links, and the DRR method performs well in this scenario 5.4 Cache efficiency

For further demonstrating the performance of the proposed method, the cache efficiency, η, is compared. The cache efficiency is defined as the ratio of the total data rates retrieved from caches to the total data rates, i.e.,

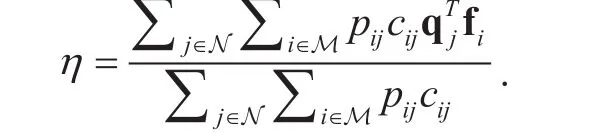
According to figure 4, the cache efficiency of DRR method is almost the same as that of CRR and CR method, and they all outperform that of max-SINR and RE method under each configuration. Moreover, with fixed S,increasing CSBSleads to reduced η. With fi xed CSBS, however, increasing S gives rise to increased η. These results are consistent with those in figure 3. When S is fixed, increasing CSBSleads to much more growth in the total data rates, no matter the total data rates retrieved from caches increase (S=20)or decrease (S=50,100). As a result, η will decrease. When CSBSis fixed, increasing S

leads to almost even increases in the numerator and denominator of η, which results in increased η.

5.5 Effects of weight

Finally, we investigate the effects of weight on the performance of the DRR method. Figure 5 shows the variations of f1(P) and f2(P) with different values of weight in DRR method. In accordance with intuition, f1(P) increases anddecreases as ω increases. In addition,when ω＞0.5 (only for this realization, different realizations may yield different values),the DRR method outperforms both max-SINR and RE method. In all the above simulations,ω=0.8 is chosen for making a trade-off between user experience and cache usage.

5.6 Effects of available bandwidth

Table 3 shows the values of the objective function with different available bandwidth B.As B increases, the values of objective function and its components, f1(P) and f2(P),also grow. Since the maximum achievable date rate cijis proportional to B, the objective function and its components, which increase monotonously with cij, are also ascending as B increases.

5.7 Effects of the scale of file library and the skew parameter

Figure 6 presents the effects of the scale of file library F and the skew parameter z on the performance of the proposed method. For given F, the value of objective function will increase as z increases. Meanwhile, for given z, the value of objective function will increase as F decreases. For smaller F and larger z, according to applied probabilistic content placement scheme, more popular contents will be cached at BSs. Hence, the probability that a user finds his/her requested content in the caches at BSs increases, and more backhaul capacity is spared for non-cached contents.Accordingly, the total network utility will grow.

VI. CONCLUSIONS

In this paper, a distributed relaxing-rounding method is proposed for user association and resource allocation in cache-enabled small cell networks. At first, the relaxed MINLP problem is solved in a distributed manner by double dual decompositions. We then round the obtained solution to derive single association solution. Finally, this single association solution is brought into the original problem and the resultant problem is solved by former distributed algorithm once again. Experimental results show that the DRR method enhances the cache efficiency drastically and improvesthe total utility of data rates as well. In addition, its solution approximates the optimal solution of the original MINLP problem well in practical scenarios.

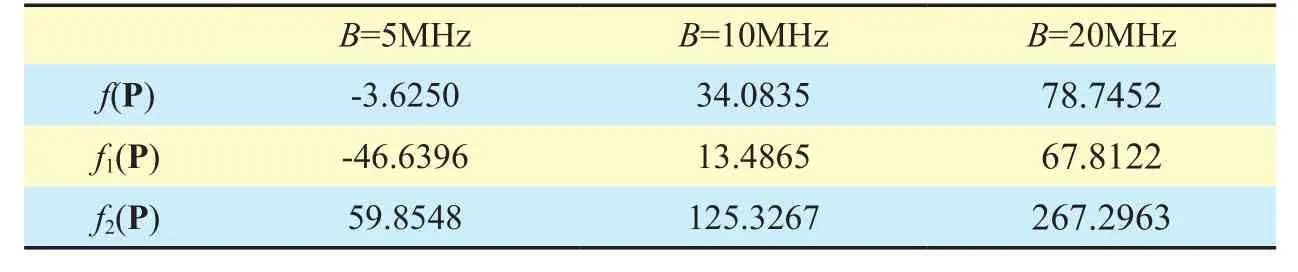
Table III The values of the objective function with different available bandwidth.S=50, CSBS=5Mbps, ω=0.8

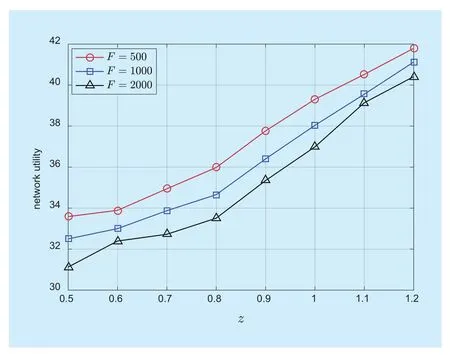
Fig. 6 The effects of the scale of file library F and the skew parameter z on the network utility. S=50, CSBS=5Mbps, ω=0.8

ACKNOWLEDGEMENTS

The authors would like to thank the reviewers for their detailed reviews and constructive comments, which have helped to improve the quality of this paper. This work is supported by National Natural Science Foundation of China under Grants No. 61371087 and 61531013, The Research Fund of Ministry of Education-China Mobile (MCM20150102).

[1] Cisco whitepaper, “Cisco Visual Networking Index: Global Mobile Data Traffic Forecast Update, 2015-2020,”[Online] available:http://www.cisco.com/c/en/us/solutions/collateral/service-provider/visual-networking-index-vni/mobile-white-paper-c11-520862.html.

[2] T. Nakamura, S. Nagata, A. Benjebbour, et al.,“Trends in small cell enhancements in LTE advanced,” IEEE Communications Magazine, vol.51, no. 2, 2013, pp. 98-105.

[3] Z. Luan, H. Qu, J. Zhao, et al., “Correntropy induced joint power and admission control algorithm for dense small cell network,” IET Communications, vol. 10, no. 16, 2016, pp. 2154-2161.

[4] J. G. Andrews, S. Buzzi, W. Choi, et al., “What will 5G be?” IEEE Journal on Selected Areas in Communications, vol. 32, no. 6, 2014, pp. 1065-1082.

[5] A. F. Molisch, G. Caire, D. Ott, et al., “Caching eliminates the wireless bottleneck in video aware wireless networks,” Advances in Electrical Engineering, vol. 2014, 2014.

[6] U. Paul, A. P. Subramanian, M. M. Buddhikot, et al., “Understanding traffic dynamics in cellular data networks,” Proc. IEEE INFOCOM, 2011, pp.882–890.

[7] M. Cha, H. Kwak, P. Rodriguez, et al., “I tube, you tube, everybody tubes: Analyzing the world’s largest user generated content video system,”Proc. ACM SIGCOMM conference on Internet measurement, 2007, pp. 1-14.

[8] M. Ji, G. Caire, A. F. Molisch, “Wireless device-to-device caching networks: Basic principles and system performance,” IEEE Journal on Selected Areas in Communications, vol. 34, no.1, 2016, pp. 176-189.

[9] N. Golrezaei, A. F. Molisch, A. G. Dimakis, et al.,“Femtocaching and device-to-device collaboration: A new architecture for wireless video distribution,” IEEE Communications Magazine, vol.51, no. 4, 2013, pp. 142-149.

[10] E. Bastug, M. Bennis, M. Debbah, “Living on the edge: The role of proactive caching in 5G wireless networks,” IEEE Communications Magazine,vol. 52, no. 8, 2014, pp. 82-89.

[11] X. Wang, M. Chen, T. Taleb, et al., “Cache in the air: Exploiting content caching and delivery techniques for 5G systems,” IEEE Communications Magazine, vol. 52, no. 2, 2014, pp. 131-139.

[12] M. Gregori, J. Gomez-Vilardebo, J. Matamoros,et al., “Wireless content caching for small cell and D2D networks,” IEEE Journal on Selected Areas in Communications, vol. 34, no. 5, 2016, pp.1222-1234.

[13] N. Golrezaei, K. Shanmugam, A. G. Dimakis,et al., “FemtoCaching: Wireless video content delivery through distributed caching helpers,”Proc. IEEE INFOCOM, 2012, pp. 1107-1115.

[14] A. Abboud, E. Bastug, K. Hamidouche, et al.,“Distributed caching in 5G networks: An alternating direction method of multipliers approach,” Proc. SPAWC, 2015, pp. 171-175.

[15] B. Blaszczyszyn, A. Giovanidis, “Optimal geographic caching in cellular networks,” Proc. IEEE ICC, 2015, pp. 3358-3363.

[16] Z. Hu, Z. Zheng, T. Wang, et al., “Caching as a service: Small-cell caching mechanism design for service providers,” IEEE Transactions on Wireless Communications, vol. 15, no. 10, 2016,pp. 6992-7004.

[17] F. Pantisano, M. Bennis, W. Saad, et al., “Match to cache: Joint user association and backhaul allocation in cache-aware small cell networks,”Proc. IEEE ICC, 2015, pp. 3082-3087.

[18] K. Poularakis, G. Iosifidis, L. Tassiulas, “Approximation algorithms for mobile data caching in small cell networks,” IEEE Transactions on Communications, vol. 62, no. 10, 2014, pp. 3665-3677.

[19] B. Dai, W. Yu, “Joint user association and content placement for cache-enabled wireless access networks,” Proc. IEEE ICASSP, 2016, pp.3521-3525.

[20] K. Wang, F. R. Yu, H. Li, “Information-centric virtualized cellular networks with device-to-device communications,” IEEE Transactions on Vehicular Technology, vol. 65, no. 11, 2016, pp. 9319-9329.

[21] Z. Luan, H. Qu, J. Zhao, et al., “Low complexity distributed max-throughput algorithm for user association in heterogeneous network,” Wireless Personal Communications, vol. 87, no. 4, 2016,pp. 1147–1156.

[22] A. Damnjanovic, J. Montojo, Y. Wei, et al., “A survey on 3GPP heterogeneous networks,” IEEE Wireless Communications, vol. 18, no. 3, 2011,pp. 10-21.

[23] Y. Ding, S. Gregov, O. Grodzevich, et al., “Discussions on normalization and other topics in multi-objective optimization,” Proc. of the Fields-MITACS Industrial Problem Solving Workshop, 2006, pp. 87-99.

[24] P. Belotti, C. Kirches, S. Leyあer, et al., “Mixed-integer nonlinear optimization,” Acta Numerica,vol. 22, 2013, pp. 1-131.

[25] S. Boyd, L. Vandenberghe, Convex Optimization.Cambridge University Press, 2004.

[26] D. P. Palomar, M. Chiang, “Alternative distributed algorithms for network utility maximization:Framework and applications,” IEEE Transactions on Automatic Control, vol. 52, no. 12, 2007, pp.2254-2269.

[27] D. P. Bertsekas, Nonlinear Programming. Athena scientific, 1999.

[28] S. Boyd, L. Xiao, A. Mutapcic, “Subgradient methods,” lecture notes of EE392o, Stanford University, Autumn Quarter 2003-2004.

[29] A. Nedic, A. Ozdaglar, “Approximate primal solutions and rate analysis for dual subgradient methods,” SIAM Journal on Optimization, vol.19, no. 4, 2009, pp. 1757-1780.

[30] A. Ghosh, R. Ratasuk, Essentials of LTE and LTE-A. Cambridge University Press, 2011.

[31] K. Poularakis, G. Iosifidis, A. Argyriou, et al.,“Caching and Operator Cooperation Policies for Layered Video Content Delivery,” Proc. IEEE INFOCOM, 2016, pp. 1-6.

[32] L. Breslau, P. Cao, L. Fan, et al., “Web caching and Zipf-like distributions: Evidence and implications,” Proc. IEEE INFOCOM, 1999, pp. 126-134.

[33] Q. Ye, B. Rong, Y. Dong, et al., “User association for load balancing in heterogeneous cellular networks,” IEEE Transactions on Wireless Communications, vol. 12, no. 6, 2013, pp. 2706-2716.

[34] D. P. Bertsekas, Convex Optimization Theory.Athena scientifi c, 2009.