矩形高层建构筑侧击雷击次数计算模型研究

孙蔡亮 张 雷 周志忠



矩形高层建构筑侧击雷击次数计算模型研究

孙蔡亮1张 雷2周志忠1

1. 莆田市气象局 2. 南平市气象局

基于引雷空间理论，以矩形高层建构筑物为对象建立侧击雷击分析模型。通过将建构筑物尺寸、闪电先导取向角概率分布函数、所在地区雷电流极性与幅值分布特征等参数引入模型，提出量化与本地化程度较高的侧击雷击次数精确算法，并给出将本模型变换为计算其他形状建构筑物侧击通用模型的方法。

引雷空间理论（CVM） 侧击雷击次数 算法 模型

本文文献[1]中的附录A给出了计算建构筑物年预计雷击次数的经验公式，该公式只考虑了建构筑物顶部所遭受的雷击，而对于建构筑物侧面的绕击则援引国际电工委员会（IEC）[2]提出“只存在很低风险”的观点加以描述，具体侧击雷击次数及发生概率没有给出确切数据。目前国内对雷电侧击的研究多围绕防护措施进行探讨[3-4]，对侧击概率即侧击次数的精确计算还未提出较为系统的计算方法。本文以矩形高层建构筑物为研究对象，利用引雷空间理论建立侧击引雷模型并形成计算方法，并借助闪电定位监测数据给出计算实例，为侧击雷击次数的量化计算提供借鉴。

1 引雷空间模型

T. Horvath于1971年首次提出引雷空间概念，后人又提出改进的电气几何模型EGM方法，即引雷空间法（collection volume method,简称CVM）。其原理是雷电先导接近地面时先导头部与地面目标间的间距以雷击距为发生击穿放电临界距离，此时雷电先导到达的这一点开始击向建筑物或者地面，所有满足上述条件的点成为定向点，定向点集合构成引雷空间，计算引雷空间内所有位置作为定向点的概率，可求得受雷击物体最终雷击率，步骤如下：

雷电先导从引雷空间体积元内定向点击向地面微分面积单元dd时发生概率为：

可以得出该面积元的年雷击率为：

在物体的整个引雷空间域内进行积分，可得其雷击率为：

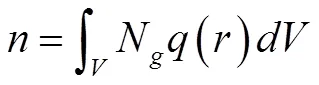
从量纲上看，上式中空间域具有面积单元，因此将其定义为等效受雷面积，其表达式为：

综合式(5)、(6)可以得到，雷击率的表达式为：

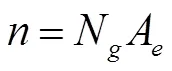
公式(1)中P()计算步骤如下：①确定雷电流幅值累积概率计算公式P()，即雷电流超过幅值的概率，可参照规程法[6]或利用闪电监测数据对IEEE及CIGER公式拟合[7-8]得到，再利用公式（5）计算出雷电流小于幅值的概率P()；②选择雷击距修正公式，此处选用Petrov[9]雷击距修正公式，即公式（6）。将公式（6）代入P()表达式,得到P()。

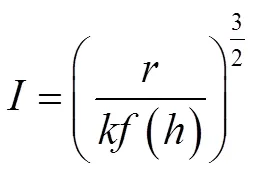
由公式（1）可得雷击距累积概率密度函数表达式：

考虑地区雷电流正负极性占比不同，根据文献[10]中加权方法处理，可得高层建构筑物侧击年雷击次数最终计算公式：

式（8）中+，-分别为正、负极性地闪发生次数占总地闪次数比例。

2 矩形高层建构筑物侧击模型

矩形高层建构筑物侧击引雷空间是将建构筑物侧立面上点作为受雷击目标，在引雷空间内根据雷击距可作出关于等雷击距的定向点曲面（如图1所示），根据其空间形状特征，将其分为两部分分别计算侧击雷击次数。第一部分为建构筑物四角处形成的四个1/4圆柱体引雷空间，将其合并后可构成完整的柱面空间（见图2）；第二部分则是由建构筑物四边向外延展的四个矩形面，将其合并后具有与建构筑物本身同样的尺寸，见图3。

由于建构筑物侧面为垂直面，因此应考虑闪电先导入射角及其概率问题，引入闪电先导在接近地面或地面上建构筑物时入射角概率分布公式[11]：

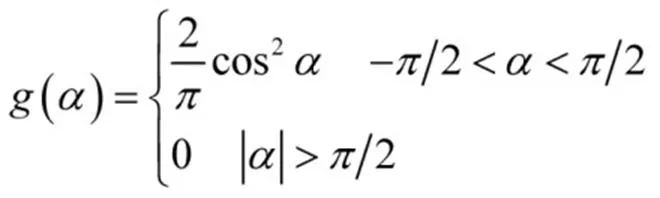
图2 四角圆弧组成的柱面空间

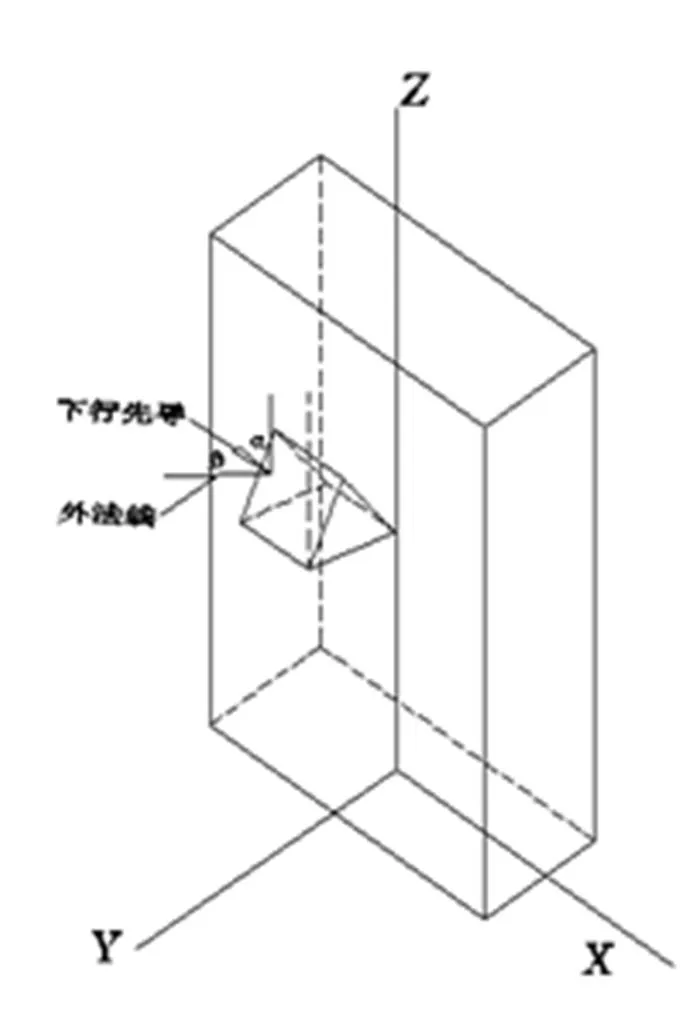
图3 矩形面组成的矩形空间

对于第一部分圆柱面，建立圆柱坐标系（见图2），圆柱面上任一曲面元d，其外法线与下行先导夹角为，面积元dS在与先导垂直的方向上的投影面积为：

面积元dS在与地面平行的水平面上投影面积为：

可得到与雷击距对应的圆柱面接闪曲面在水平方向上的等效面积为：

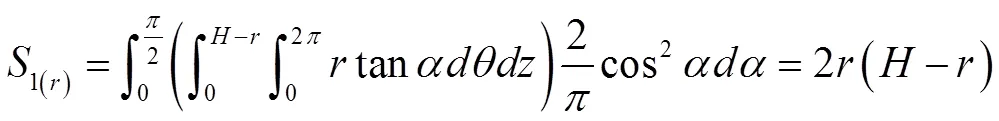
对于第二部分矩形柱面，建立直角坐标系，各面积元计算结果如下：

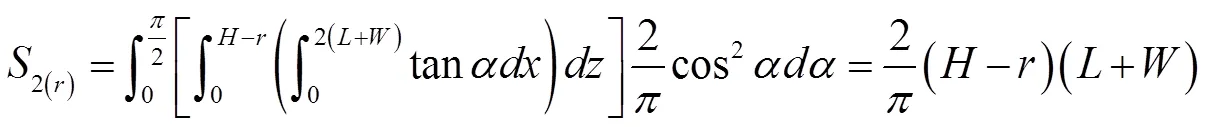
由此可得，高层矩形建构筑物与雷击距对应的接闪曲面在水平方向上的等效面积为：

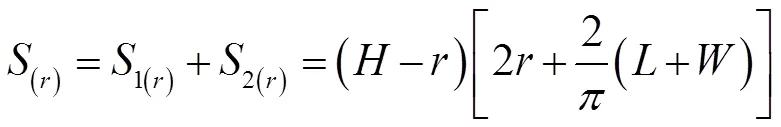
那么在雷击距的变化范围内对(r)与雷击概率密度函数q的乘积进行积分，可得到建构筑物侧击在水平方向上的等效受雷面积为：

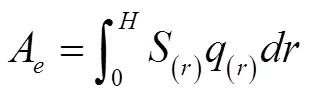
高层建构筑物侧击年雷击次数可按下式计算得到：

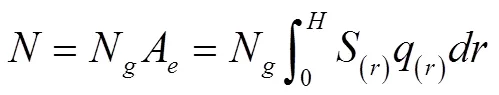
3 计算实例

以莆田市某高层矩形建筑为例，该建构筑物长=50m，宽=25m，高=100m，得到：

利用闪电定位监测数据拟合，得到莆田市雷电幅值概率函数[12]，取：

按公式（5）～（8）、（11）可求得正、负极性雷击及各项参数的最终结果，见表1。

表1 侧击雷击次数及各项参数计算结果

注：①莆田市地闪密度N数据源自《2014年福建省雷电监测公报》。

4 结果与讨论

本文提出一种计算矩形高层建构筑物侧击雷击次数的数学模型，该模型同时引入建构筑物尺寸、闪电先导取向角概率分布、所在地区雷电流极性与幅值分布特征等参数，具有较高的量化和本地化程度。

本文以矩形建筑为例建立侧击模型，从模型原理可见建筑侧击引雷空间平面图可参照文献[1]“附录A.0.3”中等效面积中的扩展部分。该模型亦用于非规则建构筑物，扩展宽度及角落处的圆弧半径即滚球半径，与矩形建构筑物不同之处在于，表达式1中对θ的积分上限由2变为建构筑物各角（外角）圆弧角度之和，表达式2()中对的积分上限由2(+)变为建构筑物边长之和。

[1] 建构筑物防雷设计规范: GB50057-2010[S].

[2] International Electrotechnical Commission．IEC62305-3: 2010．Protection Against Lightning．Part 3: Physical Damage to Structures and Life Hazard[S].

[3] 林卓宏，田军利. 高层智能大厦雷击机理及防雷设计[J].气象研究与应用，2008,29（1）:69-71.

[4] 林维勇.高层建筑物防雷[J].建筑电气，1997，16（4）:10-17.

[5] 康春华，张小青，陈校. 基于引雷空间理论的水平接闪器年雷击率预测方法[J].广东电力，2006,19（5）：15-17.

[6] 交流电气装置的过电压保护和绝缘配合: GB/T50064-2014[S].

[7] 李瑞芳，吴广宁，曹晓斌，等. 雷电流幅值概率计算公式[J].电工技术学报，2011,26（4）：161-167.

[8] 李家启，王劲松，申双和，等.基于ADTD系统监测的雷电流幅值累积概率特征分析[J].气象，2011,37（2）：226-231.

[9] Petrov N I, Water R T. Determination of the striking distance of lightning to earthed structures[J]. ProcRoy LodA, 1995(1): 589-601.

[10] Godan W B, Edwin R W.Field and analytical studies of transmission line shielding: Part Ⅱ[J].IEEE Transactions on Power Apparatus and Systems, 1969, 88(5):617-626.

[11] 魏明.雷电电磁脉冲及其防护[M].北京：国防工业出版社，2012.

[12] 孙蔡亮，王万宣，王益鑫. 基于ADTD闪电定位系统的莆田市雷电特征分析与应用[J]. 海峡科学，2014(4): 15-17.