《解决问题的策略（一一列举）》教学设计及反思

郭　奇

【教学内容】

苏教版五年级上册第94、95页的例1、“练一练”及练习十七的第1～3题。

【教学过程】

一、游戏体验策略

出示4张扑克牌。

师：同学们玩过扑克牌游戏吗？数学课上我们要玩有数学味道的扑克牌。看要求：从下面4张扑克牌中取出1张，有多少种不同的取法？（指名回答，根据学生回答板书）

师：增加一点难度，如果取出两张，有多少种不同的取法？

（学生回答。挑不全的或是随机列举、有序列举的进行对比，引导学生评价，你对他说的怎样看？为什么？你认同谁的想法，为什么？相机强调：有序、不重复、不遗漏）

如果问题变为：取出一张或两张，有多少种不同的取法？

师：刚才同学们用列举的方法把所有不同的情况都罗列了出来，一一列举（板书）就是一种解决问题的策略。好的策略可以帮助我们顺利解决问题，今天我们一起来探究：解决问题的策略（揭示课题并板书）。

二、创设情境，引出问题

师：对数学知识的认识就是从解决问题开始的。我们班的同学都很热心，特别乐意帮助别人解决问题，王大叔用木条围花圃的时候遇到了一个数学问题，你愿意帮助他解决吗？他究竟有什么困惑，我们一起去看一下吧。

出示例题：王大叔用22根1米长的木条围成一个长方形花圃，怎样围面积最大?

师：读完题目后，你想到了什么？

教师根据学生回答突出：用什么围，多少，围什么。

预设：生1：用22根1米长的木条围成的长方形周长就是22米。

生2：围成长方形的长和宽都是整米数。

生3：可以围成大小不同的长方形。

生 4：用 22÷2=11（米）可以计算出长方形的长和宽的和是11米。

师：要确定围成一个什么样的长方形，首先要考虑什么？你想怎么围？还有别的围法吗？

师：知道了长方形的长和宽的和是11米，长和宽还得是整米数，你有信心把不同的围法都找到吗？

根据学生回答小结：把不同的围法一一列举出来，计算出面积后再进行比较，最后做出回答。

三、合作交流，探索策略

1.独立探索，用一一列举的策略，结合身边的学习资源（表格提前制作），解决问题。

在学习单上完成，每一种围法的数据之间空开一定的距离。

预设：（1）长和宽颠倒的，如长2米，宽9米……引导学生理解：长方形长边的长叫做长，短边的长叫做宽，长应该比宽的长度长，长2宽9实际上就是长9宽2的长方形。

（2）没有按照一定的顺序（随机列举）。

（3）按照一定的顺序（有序一一列举）。

教师巡视，收集不同的表格。

2.汇报交流。

师：谁愿意把你的想法和大家分享一下？

学生上台在投影仪下边讲解边展示自己的表格。重点说每种情况是怎样想的，引导学生相机评价。

3.将刚才收集的不同表格在实物投影下一一展示，并分析原因。

比较（随机列举、有序列举）后，相机提问：如何能一个不漏地将所有围法都找出来？你认为可以从几开始考虑？为什么长从10米想起或是宽从1米想起？

师：你赞同哪种列举？为什么？

引导学生比较、交流，得出：一一列举时要做到有序，这样就会不重复、不遗漏。（板书：有序、不重复、不遗漏）

四、比较反思，探索规律

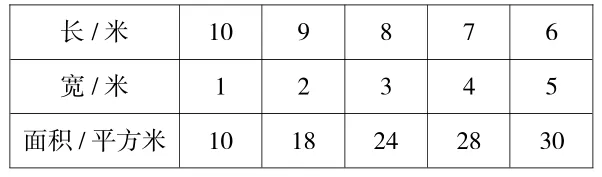
师：比较表格中的长、宽和面积，你有什么发现？

生1：我发现，长方形的长和宽相差越大，长方形的面积就越小；长和宽越接近，面积就越大。

生2：我觉得应该加一句，当周长相等时，长方形的长和宽相差越大，长方形的面积就越小；长和宽越接近，面积就越大。

生3：周长相等的长方形面积不一定相等。

小结:周长相等的长方形面积不一定相等。当周长一定时，长方形的长和宽越接近，面积就越大。

师：一一列举的策略不但能帮我们准确全面地找到答案，还让我们发现了隐藏的规律，真是一举两得。

师：回顾刚才解决问题的过程，你有什么体会？四人小组交流一下。

师：用列举的策略解决问题有什么好处？

生：可以帮助我们不重复、不遗漏地找出所有符合要求的情况。

师：运用列举的策略时要注意什么？

生：按一定的顺序思考。

五、灵活运用，提升策略

师：生活中还有很多数学问题，我们大家还能轻松地应对吗？

1.一个音乐钟，每隔一段时间就会发出优美的铃声。已经知道上午 9:00、9:40、10:20 和11:00发出铃声，那么下面哪些时刻也会发出铃声？(在正确的答案下面打“√”)

13:0014:4015:4016:00

引导学生理解题意，发现规律。

说一说你打算怎样解决这个问题？

在学习单上完成。展示交流。

提问：为什么列举到16:00，就不需要再往下列举了。

你是用什么方法完成这道题的?在列举前要先做什么？（找到规律，有序列举，根据列举，找到时间）

2.小芳有下面4枚邮票，用这些邮票能付多少种不同的邮费？

读题，理解题意。

怎么理解用这些邮票能付多少种不同的邮费？用一枚邮票能付几种不同的邮资？

在学习单上完成。展示交流，说说怎么想的？

（从选一张想起）

六、全课总结

【教学反思】

本节课注重创设生活与实践的人文情境，增强了数学课堂教学的生活情趣，让数学贴近生活，用具体生动、形象可爱的生活事例展现数学问题。

1.联系生活，唤醒学生的经验。

学生的学习是以原有的认知起点为基础的。列举的策略，在此之前学生已经有所接触，而且在不断的具体的应用过程中，学生已经体会了一一列举的基本思考方法，知道列举要注意有序，要不重复、不遗漏地进行思考，课始通过唤醒学生头脑中已有的生活经验和旧知，从而激发学生强烈的探究新知的欲望和学习的热情。

2.倡导学生自主探究新知。

有效的数学教学，应该从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程。能对信息进行分析，用“一一列举”的策略解决实际问题是本节课的教学重点。解决问题的策略只能在方法的实施过程中通过体验获得。而体验是一种心理活动，是在亲身经历的过程中获得的意识与感受。教学中让学生在已有知识经验的基础上，通过自主探究的形式去找出问题的所有答案，去发现一一列举法的好处。通过交流让不同程度的学生能在同一个层面再进行新知的学习。从而分散教学难点，培养学生自主学习的习惯。

3.合作交流让学生主体地位更加凸显。

把课堂还给学生，让学生在自主交流、自主合作中去认识新知、理解新知、掌握新知，进而用所学的知识解决实际问题。学生的创新和实践能力的培养需要这种学习形式，因此在教学过程中这种学习方式运用比较多，也收到了良好的学习效果。