如何有效促进孩子理解“为什么长乘宽等于长方形的面积”
吴旭宏

【摘 要】“为什么长乘宽等于的是长方形的面积?”这个问题重要吗?我认为很重要。首先这个问题讲述了长度、宽度和面积单位的对应关系。我们用的是长度单位,想的是面积单位的个数,它进一步理解了面积的意义。第二,会用长方形的面积计算公式计算不代表你在用二维的思维方式思考,我们应该学会长和宽两个维度去思考单位面积的个数。第三,明白这个道理,是能促进长方形的周长与面积在解决问题当中的区分。因此要让孩子明白这个道理。
【关键词】长方形的面积;前测
我有幸看到了罗永军关于长方形的面积的教学前测。作者通过给定单位面积测量面积,给定长度刻度线测量图形的面积,给出长度数值求图形的面积三个方面进行前测,统计数值正确,数值、单位都正确,有划分的痕迹,有划分且列式计算四个方面数据。
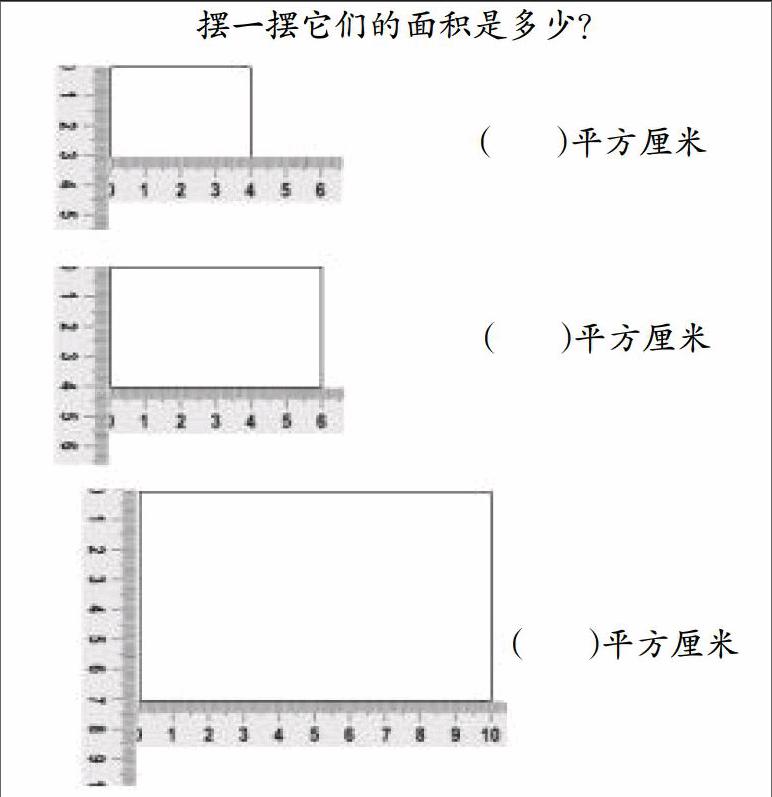
1.如果□的面积是1平方厘米,你知道下面图形的面积分别是多少?
2.如果□的面积是1平方厘米,你知道下面图形的面积分别是多少?
3.下面两个图形的单位刻度都是1厘米,你能计算它们的面积吗?
4.下面图形的面积是多少?你是怎么想的?
我用同样的前测题目,以本校学生为样本,做了一次前测。得出了和罗老师同样的结果:通过给定单位面积测量面积和给定长度刻度线测量图形的面积数值正确率很高,其它方面的正确率也不错,均在90%以上。而到了给出长度数值求图形的面积这一类题时正确率骤然下降,正确率60%不到。虽然已经前面这么多个前测题的铺垫。而且,想到划分或语言描述对应关系的孩子只有13%。这说明,要理解“为什么长乘宽等于的是长方形的面积?”难点在于想到长和宽的数值与单位面积的对应关系。
回顾自己以前的教学,想到一个细节:学生去完成书上任意几个1平方厘米拼出一个长方形,然后填表。发现有些学生在填长和宽的时候孩子都是在数小方块,也许他们并没有在数长度,而将长度和面积单位混为一谈。学生在这个环节的模糊,也许是造成之后理解的困难。
因此,为了让孩子更好地理解“为什么长乘宽等于长方形的面积”我把着力点放在2个问题上:
1. 如何让孩子容易想到长和宽的数值与面积单位的对应关系。我想到了两个材料是可能促进孩子这样的思考:(1)任意几个1平方厘米拼出一个长方形然后去引导孩子找对应的长度,直观地呈现面积单位和长度单位的练习。(2)呈现尺子,利用尺子的刻度去想到对应的面积单位。
2. 孩子从长和宽的数值想象到面积单位个数过程跨度较大,如何帮助孩子建立良好的表象,促进孩子这种想象。
我针对上面两个问题设计了前测,第一个前测具体指向上面提到的(1)号和(2)号哪种材料更能激发孩子由数值想到对应的面积单位”这个问题。第二个前测具体指向“半铺对由长宽数值想到对应的面积单位空间推理有何作用?”
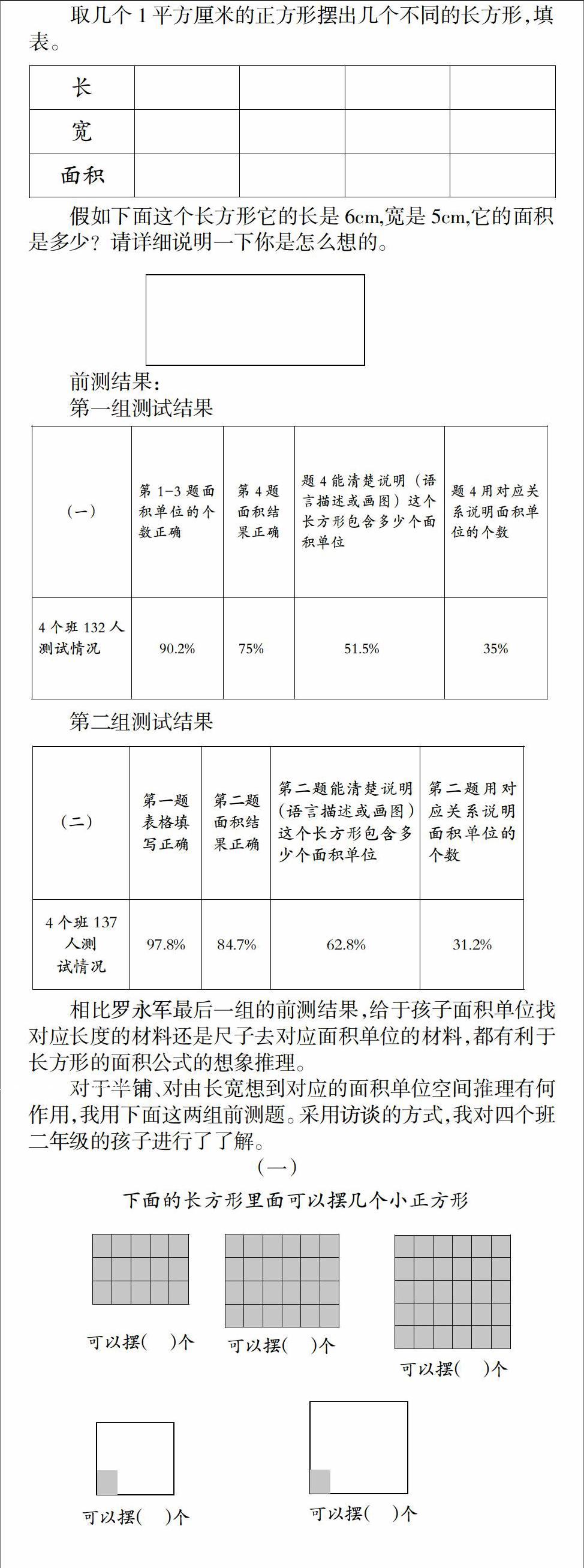
关于第一个问题,我设计了这样两组前测题。(为避免长度和面积单位的混淆,教师引导了第二组前测题的表格第一列填空,强调了“长方形的长在哪,是多少,为什么。”)
前测结果:
第一组测试结果
第二组测试结果
相比罗永军最后一组的前测结果,给于孩子面积单位找对应长度的材料还是尺子去对应面积单位的材料,都有利于长方形的面积公式的想象推理。
对于半铺、对由长宽想到对应的面积单位空间推理有何作用,我用下面这两组前测题。采用访谈的方式,我对四个班二年级的孩子进行了了解。
(一)
(二)
通过半铺的想象练习后,第4、5题的正确率有所提高。同时从访谈中感受到,“半铺”练习后,提高了孩子对第4、5题的思考速度。这样一个结果说明了人教版教材呈现的全铺—半铺—不铺教学顺序中,中间插入半铺辅助性的相象推理是有效的。
这样的前测可以给我们的教学实践一些启示。
1.人教版教材中的“取几个1平方厘米的正方形摆出几个不同的长方形,填表”活动,孩子会将横着摆的个数和长的长度概念混淆在一起。我们需要着力孩子从面积单位中分离出长度单位,厘清长度和面积单位对应关系。同样我们用一个1平方厘米的正方形去量长方形的长这样的活动,也应该是有效的。
2我们可以利用尺子测量经验和刻度直觀帮助孩子理解关键的对应关系。半铺教学之后,“不铺你还能知道长方形的面积吗”这个教学环节中,我们给予尺子直观,孩子是容易进行全铺的想象推理的。
3.教学中我们需要想象练习来完成一维到二维的飞跃。半铺就是一个很好的辅助。
我们可以加入半铺的变式练习。
可以设计两把尺子过渡到一把尺子的想象。
可以设计利用二维想象说明统一单位的必要性。

