基于GEV模型的开都河上游降水模拟

王志成

(新疆塔里木河流域管理局， 新疆 库尔勒 841000)

基于GEV模型的开都河上游降水模拟

王志成

(新疆塔里木河流域管理局， 新疆 库尔勒 841000)

基于开都河流域上游降水数据，采用GEV模型进行极值降水的模拟和分析。结果表明：AMS1序列的形状参数大于0，服从Fréchet分布；在较高重现期下由轮廓似然方法估计的置信区间比Delta方法更准确；重现水平的轮廓似然函数曲线在较高重现期之下呈较显著不对称性；基于非平稳GEV模型得到极值降水设计值，其在1958年的100年一遇设计值到2010年下降为接近50年一遇，预示着未来发生极值降水和洪灾的风险加大。

GEV模型； 极值降水； 开都河上游； 非平稳

1 引 言

全球气候变化背景下，水文气象极值事件增加的可能性已经引起全世界各国政府和学术界的关注，因为相比于平均值的变化，极值事件频率和强度的变化对自然和人类社会将产生更加意义深远的影响。极值水文气象事件对于全球气候变化的响应十分敏感，已有研究表明，当前世界上许多国家和地区的极端水文气象事件发生概率在增加。此外，在气候变化和人类活动影响越来越显著的条件下，极值水文气象数据常常表现出非平稳性，如存在显著趋势或发生突变等[1]，针对具有非平稳特征的水文气象序列如何进行模拟，已经引起了广泛的关注。

概化极值分布(Generalized Extreme Value，GEV)将Weibull分布、Gumbel分布和Fréchet分布统一起来，不必考虑原始分布类型，可以避免单独采用某一种分布的不足，因而被广泛用于极值事件的模拟。值得注意的是，在极值模拟中，GEV分布所依据的极值理论假定序列具有平稳性，然而水文气象时间序列平稳性的假定一直受到质疑[2]。叶长青等[3]研究表明，当洪水序列存在非一致性时，如果仍采用传统方法，会高估设计洪水的量级。针对此问题，谢平等[4]提出了基于时间序列分析的非一致性年径流序列水文频率计算方法；宋松柏等[5]推导了具有跳跃变异的非一致分布水文序列频率计算公式。

当前基于GEV模型进行开都河流域上游极值降水模拟方面的研究尚不多见，尤其是针对该流域极值降水序列可能存在的非平稳特征进行模拟的研究尚未开展。本文选择开都河上游巴音布鲁克气象站数据，基于GEV模型进行该流域1958—2010年极值降水演变的模拟和分析，以期有助于该区域未来洪灾风险的评估。

2 数据来源和研究方法

2.1 数据来源

数据来源于中国气象局国家气象信息中心(中国气象数据网http://cdc.cma.gov.cn)。选取流域内的巴音布鲁克气象站为典型站，逐日降水数据序列跨度为1958—2010年，提取得到逐年最大1d降水量序列(annual maximum series 1-day,AMS1)，进一步进行极值降水序列的模拟。

2.2 非平稳GEV模型

平稳GEV模型，其位置参数、尺度和形状参数是常数，不随时间而变化；而非平稳GEV模型的参数可以随时间而变化，其关系可以是线性函数，也可以是二次函数等，本文采用线性函数。位置参数和尺度参数对极值降水的变化趋势起主要作用，而形状参数的作用则较小，另外，模拟中如允许形状参数进行变化，可能造成数值计算方面的问题。因此本文将形状参数作为常数。此外，模拟时一般先考虑位置参数随时间变化，在此基础上再考虑尺度参数随时间的变化。

2.3 Delta方法与轮廓似然函数方法

置信区间的估计方法有Delta方法与轮廓似然函数方法。其中Delta方法假定参数的估计结果是对称的，但是对于形状参数和重现水平来说往往并不如此，该方法所得置信区间关于重现水平的估计值也是对称的，这在极值统计的应用时存在不足。轮廓似然函数方法是在仅对极值分布中的一部分参数感兴趣的情况下，构造感兴趣参数的置信区间。研究表明，轮廓似然函数曲线的不对称性，正好与极值变量取大值时的不确定性大于取小值时的不确定性这一特点相吻合，因此该方法的区间估计结果可以得到很大改善，优于Delta方法。

3 结果与分析

3.1 平稳序列GEV模型

首先进行序列平稳性特征的检验，主要考察其是否存在趋势或突变。计算巴音布鲁克站最大1d降水量序列的1至10阶自相关系数，由于各序列的1阶自相关系数均不显著，其他各阶自相关系数中绝大部分也不显著，因此在趋势检验中没有进行自相关系数的校正。对该站AMS1序列进行MK(Mann-Kendall)和线性趋势检验，发现其极值降水序列存在较显著的上升趋势，其MK趋势Z值和线性趋势t值分别为2.78和1.26，达到0.05显著性水平。

根据趋势和突变检验的结果，巴音布鲁克站极值降水序列存在非平稳性，适合于采用非平稳GEV模型进行模拟。对该站AMS1序列进行平稳GEV模拟，模拟诊断结果见图1。

图1 巴音布鲁克站AMS1序列GEV模拟结果诊断

图1(a)为Q-Q图，纵坐标与横坐标分别为经验和模型拟合分位数。在模拟结果非常好的情况下，数据将沿着对角线排列。可见，绝大部分点据位于对角线上，仅仅在高分位数部分有个别奇异点。图1(b)与Q-Q图很相似，但它是从拟合分布中随机取一个样本，将其分位数和实际数据的经验分位数绘制而得。其中1∶1线是当x=y时的对角线，回归直线是数据点的拟合直线，可见点据拟合线与1∶1线非常接近。图中的置信限提供了关于其尾部不确定性的直观了解，可见随着分位数增加，不确定性显著增大。分析这种不确定性可能与降水序列在1975年和2005年存在两个超大值有关。概率密度图[图1(c)]中经验和模拟的密度曲线较一致，也说明参数估计结果是合理的。从重现水平图[图1(d)]来看，所有的点据都位于95%置信区间内，且大多集中在置信区间中央的凹曲线附近，表明所构建模型是稳定可靠的；其曲线下凹也说明形状参数大于0，服从Fréchet分布。

3.2 两种方法计算的置信限

分析基于Delta方法和轮廓似然函数方法分别得到的置信区间，结果见图2。在重现期低于5年左右的情况下，Delta方法得到的置信区间在置信下限和置信上限均大于轮廓似然函数方法；重现期大于5年左右的情况下则相反，Delta方法的置信下限和置信上限均低于轮廓似然函数方法。在重现期大于100年之后，两种方法得到的置信限均较宽，反映对远超过序列长度的重现期进行推断时所产生的固有不确定性很大。但在重现期较大的情况下，轮廓似然函数方法给出的结果更加准确，因为该方法考虑了参数分布的偏态特征。此外，由图2可见，在重现期较小的情况下，Delta方法的结果与轮廓似然函数方法比较接近，也可以得到较合理的置信区间。

图2 AMS1序列重现水平

3.3 不同重现期下的极值降水

在非平稳GEV模型中，其位置参数μ是随时间变化的，因此计算得到的极值降水重现水平(极值降水设计值)也将随着时间的推移而变化，称为等效重现水平(effective return level)，它是一组数值而不是唯一确定的值，因此等效重现水平扩展了重现水平的概念。由图3可见，基于非平稳GEV模型计算得到的极值降水设计值，是随着时间的推移而不断上升的一组值，在1958年的100年一遇设计值到2010年下降为接近50年一遇，预示着未来发生极值降水和洪水的风险会加大。

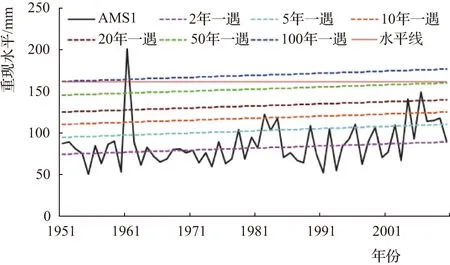
图3 基于非平稳GEV模型的AMS1重现水平序列

等效重现水平的概念，与时变矩方法计算的设计值很类似。在当前水文时间序列常常表现出明显非平稳特征的情况下，传统频率分析方法得到的设计值结果常常难以满足需求。例如，当径流序列的均值存在上升趋势时，其洪水设计值将被低估，从而造成水工建筑物的失事风险加大；反之，若存在下降趋势，设计值将被高估，从而增加建筑物的造价。

4 结 论

a.巴音布鲁克站年最大1d降水量序列(AMS1)存在显著上升趋势，该站以时间作为位置参数的协变量进行非平稳GEV模拟，似然比检验结果表明其模拟效果优于平稳GEV模型。

b.与Delta方法相比较，在较高重现期下轮廓似然函数方法给出的置信区间更准确；同时，重现水平的轮廓对数似然函数曲线在较高重现期的情况下呈较显著的不对称性。

c.采用等效重现水平的概念，基于非平稳GEV模型计算得到了不同重现期之下的巴音布鲁克站极值降水的设计值；它们分别是随着时间推移而不断上升的一组值，在1958年的100年一遇设计值到2010年下降为接近50年一遇。该结果对于评估当前气候变化下的区域极值降水与洪灾风险具有重要的启示。

[1] 顾西辉,张强,王宗志.1951—2010年珠江流域洪水极值序列平稳性特征研究[J].自然资源学报,2015,30(5):824-835.

[2] MILLY P C D,BETANCOURT J.Stationarity is dead:Whither water management[J].Science,2008(319):573-574.

[3] 叶长青,陈晓宏,张家鸣.具有趋势变异的非一致性东江流域洪水序列频率计算研究[J].自然资源学报,2013,28(12):2105-2116.

[4] 谢平,陈广才,夏军.变化环境下非一致性年径流序列的水文频率计算原理[J].武汉大学学报(工学版),2005,38(6):6-15.

[5] 宋松柏,李扬.具有跳跃变异的非一致分布水文序列频率计算方法[J].水利学报,2012,43(6):734-739,748.

Simulation of upstream precipitation of Kaidu River based on GEV model

WANG Zhicheng

(XinjiangTarimRiverBasinAdministration,Korla841000,China)

GEV model is adopted for simulation and analysis of extreme precipitation on the basis of upstream precipitation data in Kaidu River Basin. Results show that the shape parameter of AMS1 sequence is greater than 0, which is consistent with Frechet distribution. The confidence interval estimated by the profile likelihood method is more accurate than Delta method under higher return period. The profile likelihood function curve of the return level shows more prominent asymmetry under higher return period. The extreme precipitation design value is obtained on the basis of non-stationary GEV model. The once-in-a-century design value in 1958 is reduced to once-every-50 years in 2010. It indicates that the extreme precipitation and flooding risks are increased in the future.

GEV model; extreme precipitation; Kaidu River upstream area; non-stationary

10.16616/j.cnki.10-46/TV.2017.03.016

TV125

A

2096-0131(2017)03- 0052- 04