基于复杂网络Braess悖论的小区开放与否综合评价探究
段龙龙
上海工程技术大学管理学院,上海 201620
基于复杂网络Braess悖论的小区开放与否综合评价探究
段龙龙*
上海工程技术大学管理学院,上海 201620
近期,《关于进一步加强城市规划建设管理工作的若干意见》中提出推广街区制等建议,提倡开放封闭小区,引起大家广泛的关注和讨论。因此本文就小区开放对周边道路通行的影响展开研究,基于传统的阻抗加了交叉口红绿灯等待的时间对路面通行时间的影响,从而构造出来一个新的综合阻抗函数模型对小区开放进行探究。同时由于有效时间的提出,UE配流模型中时间参数也得到进一步改进。利用阻抗函数、UE配流、Braess悖论等,定量计算出小区在何种情况下开放、如何开放。并选取了一定的角度,对小区进行分类验证,定量的对比出小区开放前后对周围道路通行的影响程度,为城市规划和交通管理部门的决定提供科学有效的理论依据。 关键词:小区开放;阻抗;Braess
一、引言
为了建设美好城市,适应和引领新经济态势,实现中国梦,近期,《关于进一步加强城市规划建设管理工作的若干意见》中提出新建住宅要推广“街区制”,原则上不再建设封闭小区,已经建成的住宅小区和单位大院要逐步打开等诸多意见,事实上开放小区的主要目的是“优化街区的路网结构”,实现小区内部道路私有化变为道路公有化,疏通城市交通的“毛细血管”,从而解决目前的交通拥堵问题。但是开放小区是否能够真地高效地利用有限的道路资源,达到改善交通状况的目的呢?众人对待这个问题想法各异,各持己见,因而造成广泛热议。总体上认为小区开放是否能够提高道路通行能力,改善交通状况与小区面积,位置,内外部道路状况等诸多因素相关,不能一概而论。
二、建立模型
本文从车辆通行的角度来研究小区开放对于周边道路通行的影响,首先排除了行人的因素,并且假设此处的车辆均指机动车。其次,本文将行驶时间作为判断两地之间便捷性的最重要的标准,研究路阻函数(BPR函数),然后将其运用到新增支路,在此处,可将新增支路看做是小区开放的表现,最后使用Braess现象来判断新增支路能否缩短两地之间的行使时间,并据此来说明是否需要开放小区。
(一)基础模型
美国联邦公路局路阻函数(BPR函数)考虑了实际流量对行驶时间的影响,BPR阻抗函数为:
tij=αij+βijfij
(2.1-1)
式中:ij——从路段i到路段j;
tij——路段ij上的走行时间,单位S;
αij——路段ij上的走行时间,单位S;

fij——路段上ij的流量,单位:每小时车辆数。Vij是最大服务交通量,Cij是基本通行能力之比。
(二)模型改进建立新模型
由于传统的BPR模型只考虑了交通流量对路面通行时间的影响,这里还考虑了路口交叉口等待红绿灯的情况,即考虑了有效通行时间,交叉口平均延误计算方法[1]:
(2.1-2)
式中:T-信号周期长度,单位:s;
tg—有效绿灯时间,单位:s;
x—车道组V/C或饱和度,V/C指在理想条件下,最大服务交通量与基本通行能力之比。
行驶时间是车辆和行人判断两地之间便捷性的重要标准,通过路阻函数,获得各个时段的路阻函数之后,给新增道路分配交通量。
修正的综合BPR阻抗函数模型为:
(2.1-3)
(三)基于复杂网络的数学规划模型
我们在出行过程中,选择出行方式都是尽可能的使自己能够用最短的出行时间,实现自己的目标,故而选择UE配流模型,如下:
minZ(
(2.1-4)
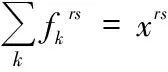
(2.1-5)
fkrs≥0 ∀r,s,k
(2.1-6)
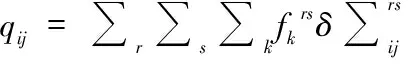
(2.1-7)
在该式中有:
qij-(i,j)路段上的流量;
tij-(i,j)路段上的时间;
xrs-研究相应时间段O-D对r-s之间的交通需求量;
fkrs-在O-D对r-s之间路径k上的流量;
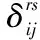
根据新构建的阻抗函数模型(2.1-3)式,其中不仅考虑了交通流对车辆路面行驶有影响,还考虑了红绿灯等待时间的影响,这也使Wardrop平衡配流原则的数学规划模型中tij这个时间更接近现实情况,从而得出更为准确的结论。
(四)基于复杂网络的Braess悖论的判断
对于封闭小区的开放问题,其实就是让非小区内部人员也可以使用小区内部的公共土地资源,其目的主要是为了缓解主干道的和次干道的交通堵塞问题,分担交通压力。与此同时,道路的增加就必然会诱发交通流的产生和增加,在一定情况下,增加道路反而起到了反作用。因此哪些情况可以增加,哪些情况不允许,是我们必须要思考的问题。为了解决这一问题,引进Braess悖论,用来判断什么情况下出现Braess现象。
Pas[5]和Principcipio二人在1997年发表的一篇论文中指出两种不会发生Braess悖论现象的情况,一种情况交通需求要求低,见式:
(2.1-8)
第二种情况交通需求要求过高,见式:
(2.1-9)
式子中:
αx-为与ij相邻或相交道路的自由通行时间,s;
αn-为路段ij上的自由通行时间;
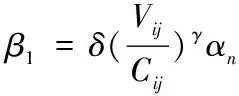
βx-在与ij个相邻或相交路段上的延误参数。

(2.2-0)
而判断是否出现Braess现象的重要依据是网络的总阻抗。网络总阻抗即为在交通网络上所有车辆的总出行的时间。其计算表达式为:
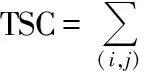
(2.1-1)
式子中:TSC-网络总阻抗;
tij-在(i,j)道路阻抗函数;ij-在(i,j)道路上的流量。
三、应用实例验证分析模型
(一)实例具体分析
封闭型小区的内部结构多样化,外部环境又受周边的道路结构、车流量、道路饱和度等因素的影响,故前文所建立的数学模型,应用不同类型的小区,那么这小区开放所产生的效果也是不同。为了能够更好的掌握什么标准条件下适合开放,什么条件下不适合,我们需要在已构建的模型的基础上,构建几种小区类型,定量比较各类型小区开放前后对道路通行的影响。
(二)小区类型构建
小区类型分类标准这里按照小区周围交通情况和小区规模大小分类:
周围交通情况:包括畅通、有拥堵可能(例如,中小学附近上学和放学时段较为拥堵);
小区规模:这里按照小区单边超过300米,或者面积大于12000平方米的时候,视为大型小区,其他视作中小型小区。
综合上述两个指标将小区分为四个类型:

表1 小区具体划分类型
(三)根据小区类型判断是否应该开放小区
1.类型I的小区

图3.3-1 开放小区前 图3.3-2 开放小区后
假设该小区周围的道路是对称的。图3.3-1的路网是由路径bad和路径bcd组成,图3.3-2在图3.3-1的基础上多出一条路径ac,已知fbc=fad=10f,fba=fcd=50f,fac=10f。假设图3.3-1中交通量为6,该交通网络中每一路径阻抗函数可以有如下表示:
tba=30+fba,tad=10+fad,tbc=10+fbc,tcd=50+fcd
其中每一路径:tbad=tba+tad,tbcd=tbc+tcd
流量为:fba=fad=fbc+fcd=3
计算出阻抗:T=3×tbad+3×tbcd=498
假使为了降低行走的总时间,而在ac两点间加一条新的线段,即为新增的路段。
忽略其他因素影响,每个路段阻抗相同,则:
同理,总时间:T′=2×tbad+2×tbcd+2×tabcd=552
从上述分析可以看出,对于小区周围交通畅通,中小型规模的小区,不需要开放该类型的小区,从设定的路阻函数值可以看出,在开放小区后,整体的阻抗值并没有减少,此时不应开发小区。
2.类型II的小区
类型II的小区周围有拥堵可能,但小区规模都是中小型的。针对此类小区,不能单就一个小区讨论,假设在一个复杂的系统中,目前有5000辆车要从节点1到节点9,如图所示:
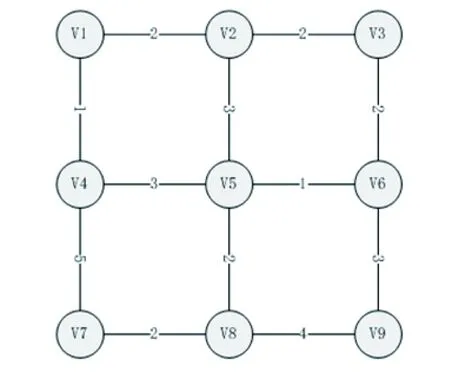
图3.3-3 复杂网络系统模拟
这里基于复杂网络的数学规划模型,最优分配交通流,假设阻抗函数分别为:
t1=x1/10+5,t2=x2/40+10,t3=x3/40+15,t4=x4/40+20,t5=x5/10+20
图中横线上所标出的数据代表了对应的阻抗函数值,由上式可以看出,阻抗函数是变量,它受选择改路同行的车辆数目的影响,在人数越多,路阻值越大,也就是要通过该路的时间越长。建模的整体目标是希望这5000辆车从节点1到节点9的总阻抗值最小,即是从系统整体视角出发,整体花费的时间越少越好。
因此这里采用具体程序,在最优化分配后,可以计算出,这些人通过该段路的最短时间。
3.类型III型小区
该类型小区周围交通畅通,小区规模较大,此时是否应该打开小区需要具体分析。从复杂交通网络中截取一个单位部分,即以一个四路段网络(可看做是未开放前的小区)为例。它的四个节点分别是A、B、C、D,起点为A,终点为B,如图3.3-1所示。图3.3-2是在原有基础上增加一条路段成为五路段网络(可看做开放后的小区)示意图。设为交通的需求,并且是一常量,且路径是呈对称分布的,并在AC路段和BD路段具有零自由流时间,路段时间是路段交通流的增函数。已知路段时间不仅与本路的路段流量有关,而且也与同一路径并且与之相邻的路段流量有关系。
(1)四路段交通网络

图3.3-4 四路段网络 图3.3-5 五路段交通网络
tAC=β1(γfAC+fCD)tAB=α1+β2(γfAB+fBD)
tBD=β2(γfBD+fAB)tCD=α1+β2(γfCD+fAC)
在上述公式中,tAD是起点A到终点D的路径K的行驶时间:
t1=tAC+tCDt2=tAB+tBD
fk是起点A到终点D路径K的交通流量:
fAC=fCD=f1fAB=fBD=f2
由于网络是具有对称性的,可得在状UE态下的路径行驶时间为:
由上可得,四路段的总的阻抗为:
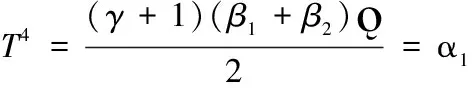
(2)五路段交通网络对UE求解
路段AB与BD之间增加了一条新的同一路径的相邻路段,表示为CB,如图3.3-5。
此时路段的阻抗函数是:
tAC=β1(γfAC+fCD+fCB),tCD=α1+β2(γfCB+fAC+fBD),tBD=β1(γfBD+fAB+fCB),tCB=α2+β2(γfCB+fAC+fBD),tAB=α1+β2(γfAB+fBD)
新的阻抗函数表示如下:t3=tAC+tBC+tBD
路段和路径的交通流的关系为:fAC=f1+f3fCD=f1fAB=f2, fBD=f2+f3fCB=f3
在UE状态下,求出五路段网络的解,令t1=t2=t3,得出如下的路径流量:
径流量:
f3=
路径时间为:
当f1=f2=0时,f3=,可得≤

当三条路径都存在交通流时,可得
增加路段CD后的网络总阻抗为:T5=f1t1+f2t2+f3t3
T5=(2γβ1+2β1+2β2+γβ2)2+α2,ifQ≤
T5=
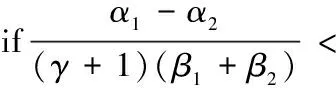
(3)是否出现悖论现象判断
如果发生了Braess悖论,即会存在T5>T4,此时:
因此,类型III的小区是否要开放,需要具体分析,并选择恰当的路口,如果路口选择不恰当,可能会出现开放小区后,反而出现交通拥堵的可能。
4.类型IV的小区
该类小区规模大,周围交通拥堵,可能是由于小区占地面积大,影响了当地的交通情况,此时建议开放该类型的小区。下表给出了小区开放前后的模拟参数。
不同类型的小区周边道路水平产生的参数处于一定的区间之间,为了简便计算和分析,取个区间的中值作为研究数据。
假设自由流速为100%,行驶速度比率近似为通行车辆在某一段路上的流量。
本文以中国道路服务水平为准,作为小区周边道路状况的评价指标,模拟数据如下表所示:
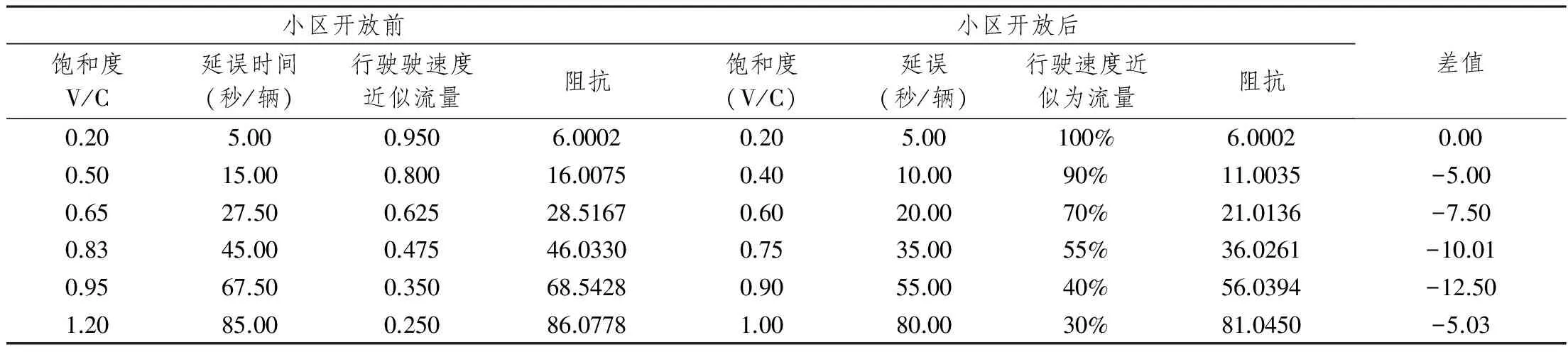
表2 模拟小区开放时的参数
结果分析,由小区内外道路的阻抗差值可得,随道路服务水平各影响参数的变化,在某一等级的道路服务水平时,小区开放总是对于车辆通行有益,且但是有益的程度随小区周边交通道路状况的糟糕程度逐渐增加,但是增加到一定程度时,益处越来越小,即产生悖论现象。
四、结束语
由本文所构建的评价指标体系和模型分析,对于结构多样的小区来说,小区开放与否和其是否真正降低主干道、次干道的交通压力,保证新增道路的饱和度在可接受范围内,在复杂网络中满足每条支路上的流量在最大程度上得到合理的安排相关,我们并不能一概而论。从交通通行角度看,如果小区开放,车辆出行的总时间减少,总的道路阻抗减少,那我们就可以说这是可实行的。
与此同时,除上述条件之外,还有诸多其他因素会影响到小区的开放,如:平均运行速度;路面饱和度;高峰小时数;交叉口排队长度等等,据此,本文针对这些因素指标,对城市规划部门和交通管理部门提出一些关于是否开放小区的意见或建议。
(一)进行小区选择的时候,封闭型小区必须保证其内部可用的道路资源丰富,且内部结构和小区性质适合对外实行交通开放。
(二)进行小区选择的时候,封闭型的需处于交通拥堵地段,且居民的出行方式严重影响到主路的交通。
(三)交通开放的小区的入口、小区内部道路修整、小区停车场出入口等改善或者重新改造时,要保证人与车能够的生命安全,同时不影响出行时对主路交通的影响。
(四)并不是增加的道路越多,路网密度增加,道路面积提高,就可以改变交通拥堵问题,每一条新增的路段都会诱发新的交通量,一旦车流量超过小区内部街道所承受的范围,那么开放小区而只会起到反作用。
[1]任福田,刘晓明,荣建.交通工程学[M].北京:人民交通出版社,2008,169-170.
[2]Pas.E,Principio S.Braess'paradox:some new insight[J].Transept Res.B,1997(3):265-276.
[3]李向朋.城市交通拥堵对策——封闭型小区交通开放研究[D].长沙理工大学,硕士学位论文,2014.
[4]贾晓敏,城市道路通行能力影响因素研究[D].长安大学,硕士学位论文,2009.
[5]刘巍,曾庆山.基于复杂网络的Braess悖论现象[J].计算机工程与设计,2015,4:1098-1102.
段龙龙,男,汉族,甘肃庆阳人,上海工程技术大学管理学院,财务管理专业本科生,研究方向:财务管理。
O
A
1006-0049-(2017)08-0009-03

