Neveu-SchwarzLoop代数的导子和自同构

祁杰，付佳媛，张志兰

(中国传媒大学理工学部，北京 100024)

Neveu-SchwarzLoop代数的导子和自同构

祁杰，付佳媛，张志兰

(中国传媒大学理工学部，北京 100024)

讨论了一类超代数：N=2的Neveu-SchwarzLoop代数的结构，具体研究了其导子代数和自同构。

Neveu-Schwarz代数；Loop；导子代数；自同构

1 引言

21世纪以来，数学家们通过研究推广Virasoro代数到超代数，发现了Neveu-Schwarz代数。随着研究的深入，Neveu-Schwarz代数的最小模、超正则变换、自同构群及超共型代数的结构等都有了相对完善的结论。特别在2014年，吴合楠结合Loop结构，给出了阶化的Virasoro Loop 代数结构。

本文拟讨论Neveu-Schwarz Loop代数的结构，主要研究其非零次导子、零次偶导子及自同构的具体作用。

2 预备知识

现在，我们介绍一些与Neveu-SchwarzLoop代数相关的基本定义及结果。

定义1 如果一个代数A可表示成子空间Am，m∈的直和：使得Am·An⊂Am+n，∀m，n∈则称A是-分次代数，称Am的元素为m次齐次元。

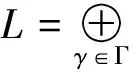
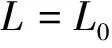
[x，y]=-(-1)αβ[y，x]；

(-1)αγ[x，[y，z]]+(-1)αβ[y，[z，x]]+(-1)βγ[z，[x，y]]=0，

其中x∈Lα，y∈Lβ，z∈Lγ，α，β，γ∈2，这时称L是域F上的一个李超代数。

定义4 若L是域F上的李超代数，D是L上的一个线性变换。如果D满足下述条件：

D([x，y])=[D(x)，y]+(-1)αξ[x，D(y)]，x∈Lξ，y∈L，α，ξ∈?2，

这时称D是L的一个超导子。记

DerL={D∈gl(L)|D是L的超导子}。

定义5 设L是域F上的李超代数，ad是L上的一个线性变换。对每一个x∈L，所有的y∈L，都有等式(adx)(y)=[x，y]，成立，这时称adx是L的超内导子。所有内导子的集合adL，称为内导子代数。对于D∈(DerL)(adL)，称D为L的外导子。商代数(DerL)/(adL)称L的外导子代数。

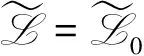
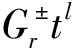
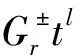
(2.1)

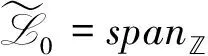
3 Neveu-Schwarz Loop代数的导子代数

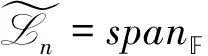
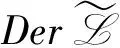
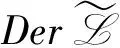
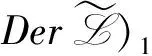
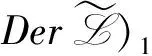
D([Litk，Ljtl])=[D(Litk)，Ljtl]+[Litk，D(Ljtl)]，D([Litk，Hjtl])=[D(Litk)，Hjtl]+[Litk，D(Hjtl)]

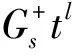
设

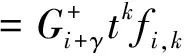
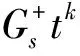
其中{i，j，k∈，r，s∈}，γ∈2。

令i=0，k=0，则

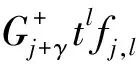
即

D(Ljtl)=[γ-1D(L0)，Ljtl]=adγ-1D(L0)(Ljtl)，

类似可以得到

D(Hjtl)=[γ-1D(L0)，Hjtl]=adγ-1D(L0)(Hjtl)，

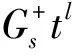
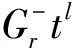
由上述可见

D=adγ-1D(L0).

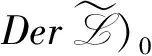
证明：类似引理3.2证明，这里不加以说明。

结合引理3.2和引理3.3，可以得到以下结论：

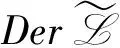
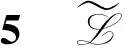
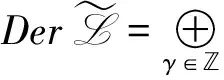
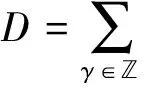
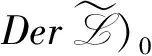
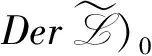
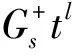
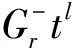
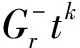
设

D(Litk)=Litkfi，k(t)+Hitkgi，k(t)，D(Hjtk)=Ljtkhj，k(t)+Hjtkpj，k(t)，

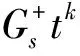
其中{i，j，k∈，r，s∈}。

由导子定义运算可得

(i-j)fi+j，k+l(t)=(i-j)fi，k(t)+(i-j)fj，l(t)，(i-j)gi+j，k+l(t)=igi，k(t)-jgj，l(t)，

(-j)hi+j，k+l(t)=(i-j)hj，l(t)，(-j)pi+j，k+l(t)=(-j)fi，k(t)+(-j)pj，l(t)，

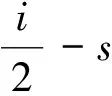
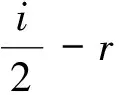
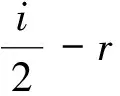
2gr+s，k+l(t)-(r-s)pr+s，k+l(t)=-(r-s)wr，k(t)-(r-s)qs，l(t)，

如果i≠j，则

fi+j，k+l(t)=fi，k(t)+fj，l(t)，

(3.1)

如果i=0，k=0，那么

f0，0(t)=g0，0(t)=us，l(t)=vr，l(t)=0，

(3.2)

如果j=0，k=l=0，i≠0，则

h0，0(t)=0，

如果i=-j≠0，k=l=0，则

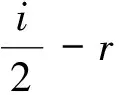
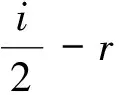
2gr+s，0(t)-(r-s)pr+s，0(t)=-(r-s)wr，0(t)-(r-s)qs，0(t)，

取m∈，m≠0，m≠i，m≠-j，且i+m≠j-m，那么有

fi+j，k+l(t)=fi+m，k(t)+fj-m，l(t)，fi+m，k(t)=fi，k(t)+fm，0(t)，fj-m，l(t)=f-m，0(t)+fj，l(t)，

那么

fi+j，k+l(t)=fi+m，k(t)+fj-m，l(t)=fi，k(t)+fm，0(t)+f-m，0(t)+fj，l(t)=fi，k(t)+fj，l(t)，

即对于任意的i，j∈，都有

fi+j，k+l(t)=fi，k(t)+fj，l(t)。

(3.3)

由上述等式可得到

如果j≠0，k≠0，l=0，那么(-j)hi+j，k(t)=(i-j)hj，0(t)=0，从而hi+j，k(t)=0，即

hi，k(t)=0，

(3.4)

将(3.4) 代入上述等式可知

qi+s，k+l(t)=pi，k(t)+qs，l(t)，wi+r，k+l(t)=pi，k(t)+wr，l(t)，fr+s，k+l(t)=wr，k(t)+qs，l(t)，

变形可得2gi，k(t)=(r-s)(qi+s，k+l(t)-qs，l(t)-fi，k(t))=(r-s)(pi，k(t)-fi，k(t))=(r-s)p0，0(t)=0，

即

gi，k(t)=0，

(3.5)

由(3.3)代入上述等式可得

qi+s，k+l(t)=fi，k(t)+qs，l(t)，wi+r，k+l(t)=fi，k(t)+wr，l(t)，pr+s，k+l(t)=wr，k(t)+qs，l(t)，

比较得

fi，k(t)=pi，k(t)，

(3.6)

由前面等式可知

fr+s+2i，k+l(t)=wi+r，k+l(t)+qi+s，0(t)，fr+s+2i，k+l(t)=wi+r，0(t)+qi+s，k+l(t)，

化简得fi，k(t)=wi+r，k+l(t)-wr，l(t)=-qi+s，0(t)+qs，k(t)+f2i，0(t)，即

qs，k(t)=fi，k(t)+qi+s，0(t)-f2i，0(t)=fi，k(t)+fi，o(t)+qs，0(t)-(fi，0(t)+fi，0(t))=f0，k(t)+qs，0(t)，

即有

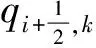
(3.7)

类似可得fi，k(t)=qi+s，k+l-qs，l(t)=-wi+r，0(t)+wr，k(t)+f2i，0(t)，即

wr，k(t)=wi+r，0(t)+fi，k(t)-f2i，0(t)=fi，k(t)+fi，0(t)+wr，0(t)-2fi，0(t)=f0，k(t)+wr，0(t)，

即有

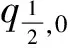
(3.8)

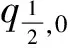
D(Litk)=Litkfi，k(t)，D(Hitk)=Hitkfi，k(t)，

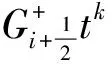
由(3.3)可得fi，k(t)=fi，0(t)+f0，k(t)=if1，0(t)+kf0，1(t)，令f1(t)=f1，0(t)，f2(t)=f0，1(t)，则

fi，k(t)=if1(t)+kf2(t)。

由

ad(H0)(Litk)=[H0，Litk]=0，ad(H0)(Hitk)=[H0，Hitk]=0，

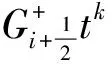
令D′=D-q(t)ad(H0)，则

D′(Litk)=(D-q(t)ad(H0))(Litk)=Litkfi，k(t)=Litk(if1(t)+kf2(t))，

D′(Hitk)=(D-q(t)ad(H0))(Hitk)=Hitkfi，k(t)=Hitk(if1(t)+kf2(t))，

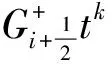
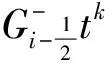
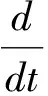
其中i，k∈。

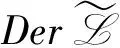
定义Hom(，F[t，t-1])是群(，+)到群(F[t，t-1]，+)的同态，取ψ∈Hom(，F[t，t-1])，满足ψ(i)=if1(t)，即ψ(i+j)=ψ(i)+ψ(j)。令Dψ=D′-Dρ，则

Dψ(Litk)=(D′-Dρ)(Litk)=Litkif1(t)，Dψ(Hitk)=(D′-Dρ)(Hitk)=Hitkif1(t)，

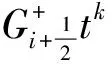
即

D=D′+q(t)ad(H0)=Dψ+Dρ+q(t)ad(H0)，

故D是外导子。

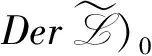
其中Hom(，F[t，t-1])∩F[t，t-1]{0}，F[t，t-1]∩()={0}，且

D∈Hom(，F[t，t-1])∩()当且仅当D=Dψ，其中ψ(i)=-ix(t)，x(t)∈F[t，t-1]。

证明：取D1∈Hom(，F[t，t-1])∩F[t，t-1]，即存在这样一个D1=Dψ=Dρ，满足

Dψ(Litk)=Litkfi，k(t)=Litkψ(i)，Dψ(Hitk)=Hitkfi，k(t)=Hitkψ(i)，

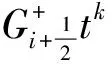
Dρ(Litk)=Liρ(tk)，Dρ(Hitk)=Hiρ(tk)，

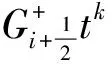
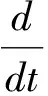
Hom(，F[t，t-1])∩F[t，t-1]{0}。

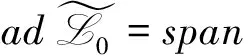
D2(Litk)=-ix(t)Litk，D2(Hitk)=-ix(t)Hitk，

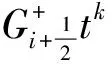
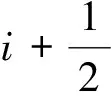
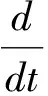
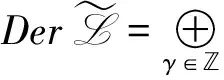
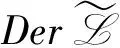
4 Neveu-Schwarz Loop代数的自同构

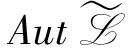
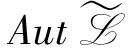
σ(L0)，σ(H0)∈spanF{L0，H0}。

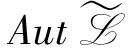
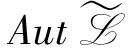
σ(Litk)=εLεiφi，k(t)+bHεiφi，k(t)，

σ(Hitk)=ξHεiφi，k(t)，

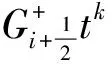
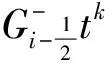
且φi+j，k+l(t)=φi.k(t)φj，l(t)，其中i，j，k，l∈，。

证明：由引理3.2可设

σ(L0)=aL0+bH0，其中a，b∈F，

a[L0，σ(xi)]=-iσ(xi)。

事实上，a≠0。如果a=0，则-iσ(xi)=0，对任意的i∈，有σ(xi)=0，显然，这与σ∈相矛盾，故a≠0，即[L0，σ(xi)]σ(xi)，因此∈，σ(xi)∈，由于对所有的i∈，都有∈成立，则a=±1，此时σ(xi)∈L±i。

情形1 如果a=1，则

σ(L0)=L0+bH0，σ(xi)∈Li，

故设

σ(Litk)=Lifi，k(t)+Higi，k(t)，σ(Hitk)=Lihi，k(t)+Hipi，k(t)，

将σ作用在(1)两边，有

(i-j)fi+j，k+l(t)=(i-j)fi，k(t)fj，l(t)，(i-j)gi+j，k+l(t)=igi，k(t)fj，l(t)-jfi，k(t)gj，l(t)。

(i-j)hi，k(t)hj，l(t)=0，ipi，k(t)hj，l(t)-jpj，l(t)hi，k(t)=0，

如果存在i0∈，使得hi0，k(t)≠0，则对所有的j∈{i0，0}，都有hj，l(t)=pj，l(t)=0成立，显然与σ∈相矛盾。因此，hi，k(t)=0对所有i∈都成立，故σ(Hitk)=Hipi，k(t)。

设

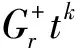
将σ作用在(1)两边，有(b-m1+r)qr，k，m1(t)=0，(b+n1-r)ur，k，n1(t)=0，由于qr，k，m1(t)与ur，k，n1(t)不全为0，故b-m1+r=0，b+n1-r=0，即m1=b+r，n1=r-b，于是

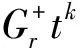
类似的可以得到

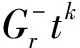
将σ作用在(1)两边得

qi+r，k+l(t)=pi，k(t)qr，l(t)，ui+r，k+l(t)=-pi，k(t)ur，l(t)。

vi+r，k+l(t)=-pi，k(t)vr，l(t)，wi+r，k+l(t)=pi，k(t)wr，l(t)。

显然，qr，k(t)与ur，k(t)之间必有一个为0，vr，k(t)与wr，k(t)之间也必有一个为0，如果qr，k(t)与ur，k(t)都不为0，则当i=0，k=0时，由qr，l(t)=p0，0(t)qr，l(t)，可知p0，0(t)=1，由ur，l(t)=-p0，0(t)ur，l(t)，可知p0，0(t)=-1，矛盾。故qr，k(t)与ur，k(t)之间必有一个为0，同理vr，k(t)与wr，k(t)之间也必有一个为0。

子情形1.1 若qr，k(t)≠0，ur，k(t)=0，即p0，0(t)=1，vr，k(t)=0，wr，k(t)≠0，满足：

qi+r，k+l(t)=pi，k(t)qr，l(t)，wi+r，k+l(t)=pi，k(t)wr，l(t)，

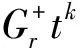
将σ作用在(1)两边，有

fr+s，k+l(t)=wr，k(t)qs，l(t)，2gr+s，k+l(t)-(r-s)pr+s，k+l(t)=-(r-s-2b)wr，k(t)qs，l(t)，

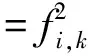
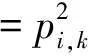
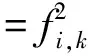
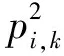
2gr+s，k+l(t)=(r-s)pr+s，k+l(t)-(r-s-2b)wr，k(t)qs，l(t)=2bfr+s，k+l(t)，

即

gi，k(t)=bfi，k(t)，

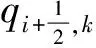
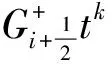
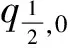
其中fi，k(t)∈F[t，t-1]，，u(t)∈F[t，t-1]*，i，k∈，且fi+j，k+l(t)=fi.k(t)fj，l(t)。

子情形1.2 若ur，k(t)≠0，qr，k(t)=0，有

其中fi，k(t)∈F[t，t-1]，b∈F，u(t)∈F[t，t-1]*，i，k∈，且满足fi+j，k+l(t)=fi.k(t)fj，l(t)。

情形2 如果a=-1，则

σ(L0)=-L0+bH0，σ(xi)∈L-i，

故设

σ(Litk)=L-ifi，k(t)+H-igi，k(t)，σ(Hitk)=L-ihi，k(t)+H-ipi，k(t)，

用同样的方法讨论，可以得到下面子情形

子情形2.1 若qr，k(t)≠0，ur，k(t)=0，有

其中gi，k(t)∈F[t，t-1]，，q(t)∈F[t，t-1]*，i，k∈，且gi+j，k+l(t)=gi.k(t)gj，l(t)。

子情形2.2 若ur，k(t)≠0，qr，k(t)=0，有

其中gi，k(t)∈F[t，t-1]，b∈F，u(t)∈F[t，t-1]*，i，k∈，且gi+j，k+l(t)=gi.k(t)gj，l(t)。

由上可知：对任意的σ∈AutL，存在x(t)∈F[t，t-1]，φ∈Hom(×，F[t，t-1]*)，ξ，ε∈{±1}，b∈F，使得

σ(Litk)=εLεiφi，k(t)+bHεiφi，k(t)，

σ(Hitk)=ξHεiφi，k(t)，

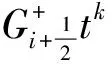
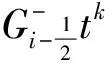
且φi+j，k+l(t)=φi.k(t)φj，l(t)，其中i，j，k，l∈，。

5 结论

[1]HenanWu，SongWang，XiaoqingYue.StructuresofGeneralizedLoopVirasoroAlgebras[J].CommunicationsinAlgebra，2014，42(4)：1545-1558.

[2]JiayuanFu，QifenJiang，YucaiSu.ClassificationofModulesofTheIntermediateSeriesoverRamondN=2SuperconformalAlgebras[J].JournalofMathematicalPhysics，2007，48，043508.

[3]JiayuanFu，YongcunGao.TheDerivationAlgebraandAutomorphismGroupofTheGeneralizedRamondN=2SuperconformalAlgebra[DB/OL].arXiv：0811.3306v1 [mathRT] 20，Nov，2008.

[4]JiayuanFu，ShaoXia，TanXiao.TheStructureofNeveu-SchwarzN=2SupercomformalAlgebra[J].中国传媒大学学报(自然科学版)，2014，21(3)：32-41.

(责任编辑：王谦)

Derivations and Automorphism of Loop Neveu-Schwarz Algebras

QI Jie，FU Jia-yuan，ZHANG Zhi-lan

(Faculty of Science and Techonology，Communication University of China，Beijing 100024，China)

This paper discusses a class structure of super algebraic：N=2Neveu-Schwarz Loop algebra，and study its derivation algebras and the automorphism.

Neveu-Schwarz algebra；Loop；derivation algebra；automorphism

2016-04-22

国家自然科学基金(HG1308)；中国传媒大学理工科规划项目(3132014XNL1403)

祁杰(1989-)，男(汉族)，江苏盐城人，中国传媒大学硕士研究生.E-mail：qizhengjie3296@sina.com

O

A

1673-4793(2017)01-0051-10