基于有限差分法的二维抛物方程的电波传播预测

王瑞东，逯贵祯

(中国传媒大学 信息工程学院，北京 100024)

基于有限差分法的二维抛物方程的电波传播预测

王瑞东，逯贵祯

(中国传媒大学 信息工程学院，北京 100024)

抛物方程方法作为一种介于射线跟踪方法和波动方程全波方法之间的一种方法，具有适用于大范围计算和兼顾计算精度的双重优点。本文首先分析了二维抛物方程的导出，在此基础之上采用有限差分法对二维抛物方程进行了差分近似，得到了可以进行数值求解的矩阵方程。为了验证该差分方法，用其对经典的单刃峰绕射和双刃峰绕射问题进行了数值计算。为了验证计算结果的有效性，建立了室内缩比测试环境，进行了实验测量。对比分析发现，该方法计算结果与实验结果基本一致。

电波传播；抛物方程；有限差分法

1 引言

在无线通信和广播电视传输技术的研究中，复杂地形条件下的电波传播预测一直是电波传播领域中的研究热点。在复杂地形环境中，无线通信和广播电视中的电波传播包括视距传播、反射传播、散射传播等多种传输方式。由于多种传输机制的存在以及计算范围大的特点，因此极大的增加了复杂地形中电波传播预测的困难。尽管如此，但是出于工程技术上的需要，电波传播研究工作者们还是建立了很多电波传播的预测模型。这些电波传播的预测模型主要可以分为经验模型和确定性模型两种。

经验模型是通过对大量的实测数据的统计分析，归纳总结得出的计算公式。这其中比较典型的有ITU-R.P1546模型和Okumura-Hata模型。P1546模型适用于频率范围在30Mhz至3000Mhz，有效发射天线高度小于3000m、路径长度在1-1000km之间的陆地路径、海面路径和陆地海面混合路径上的无线电波预测[1]。Hata模型是在Okumura大量测试数据的基础上用公式拟合得到的，适用于发射天线频率在150Mhz到1500Mhz的大型城市传播环境，对其它的传播环境和地形条件等因素用校正因子加以修正[2]。经验模型的优点是方法简单，计算时不需要详细的地形环境信息。缺点是对于路径损耗的预测精度不是很高。

确定性模型是从麦克斯韦方程组导出的计算公式。根据电磁波传播的初始条件和边界条件，求解这些计算公式就可得到传播路径上的电磁波传播特性。初始条件由发射天线决定，一般相对固定，边界条件则是由传播媒质与地表分界面的形状和电磁特性决定，通常随着传播环境的变化而不同。目前，大部分确定性模型都是基于射线追踪的电磁方法，如物理光学法(PO)、几何光学法(GO)、几何绕射理论(GTU)、一致绕射理论(UTD)等。射线追踪法师基于高频场的“局部性”，将电磁波在路径上的传播简化为直射、反射和绕射波，这样便可根据地形环境信息搜索主要传输路径，再根据各路径对场的贡献最终求得总得场强。这类模型中比较典型的有Longly-Rice模型和Durkin模型。Longly-Rice模型也被称为不规则地面模型，它预测了在自由空间中由地形的非规则性造成的电波传播衰减。该模型主要使用于频段为20Mhz到40Ghz，传输路径长度为1km到2000km的情况。Durkin模型给出了不规则地形的场强预测方法。该模型适用于计算大尺度电波传播问题，同时还可以计算不规则遮挡物体造成的损耗[3]。由于射线跟踪方法要根据地形的面、棱和顶点的位置来搜索主要的传播路径，因此，当不规则地形或建筑物表面上的面、棱和顶点数目巨大时，需要跟踪的射线就非常多，从而使得计算非常复杂。此外，还有一些不常用的小尺度电波传播模型，如积分方程法(IE)和时域有限差分法(FD)，由于计算量太大，只能计算结构简单的小区域或室内电波传播问题。总体来说，确定性模型的缺点是计算过程复杂，计算量大，优点是计算精确度高[4]。

抛物方程方法作为一种介于全波方法和射线方法之间的电波传输损耗计算方法，最近成为了一个研究的热点。抛物方程方法既能精确处理复杂地形边界条件，又能处理复杂大气波导结构，因而在移动通信和广播电视覆盖的电波传输研究中具有重要的应用价值。相比于全波方法，抛物方程方法把原波动方程转化为单向传输的偏微分方程，这样可以通过在传输方向步进的方法求解方程，降低了求解全波方程的计算复杂度。抛物方程方法最早的应用是在1946年，Leontovich and Fock用抛物方程分析了电磁波在非均匀大气中的传播问题。在1977年，Tappert在声学研究中采用分步傅里叶变换方法求解抛物方程，表明了抛物方程方法在求解大范围传播问题的潜力。James R.Kuttler 在1991年将分步傅里叶变换方法用于分析对流层大气波导的电波传播问题[5]。为了分析阻抗边界条件的电波传播问题，1996年Dockery引入了混合型分步傅里叶变换方法[6]。

本文首先分析了二维抛物方程的导出，在此基础之上采用有限差分法对二维抛物方程进行了差分近似，得到了可以进行数值求解的矩阵方程。然后将差分格式的二维抛物方程应用于单刃峰和双刃电波传播问题预测中。通常有限差分方法用于中等规模的计算问题，该方法的最大优点在于能够模拟复杂的地形边界条件。为了验证计算结果的有效性，搭建了室内实验测量平台，对计算结果进行了实验验证。

2 理论分析

在二维直角坐标系下，电波传播满足以下二维波动方程

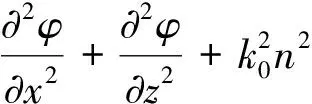
(1)

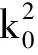
假设电磁波以很小角度沿x轴正向传播，于是可作如下近似

u(x，z)=φ(x，z)e-jk0x

(2)

代入方程(1)得

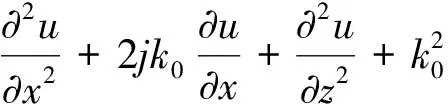
(3)

方程(3)剥离了快速变化的相位部分，因此u关于x的二阶导数远小于一阶导数

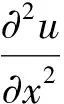
(4)

忽略关于x的二阶导数项，并近似认为大气折射率n=1，于是可得如下二维抛物方程

(5)

对方程(5)用Crank-Nicolson有限差分法[7]进行离散，

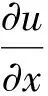
(6)

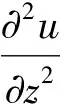
(7)

其中△x和△z分别为x方向和z方向的离散步长。

将式(6)和(7)带入方程(5)得如下矩阵方程

u(xm，zj+1)+(a-2)·u(xm，zj)+u(xm，zj-1)=a·u(xm-1，zj)

(8)

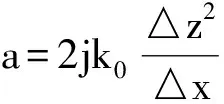
3 数值计算和实验对比

多刃峰障碍物的绕射问题是一个典型的复杂环境电波传播问题。许多实际电波传播的预测公式都是在单刃峰绕射的基础上进行改进的结果。下面选择刃峰绕射问题验证以上所述的计算方法。我们从抛物方程计算和实验测量两个方面进行比较分析。实验测量采用缩比模型在实验室环境下研究刃峰的电波绕射问题。实验配置如图1所示，实验平台搭建在理想导体平面上，周围采用吸波材料包围。实验中工作频率选择9.35GHz，发射天线采用单极子天线，接收天线采用波导天线。

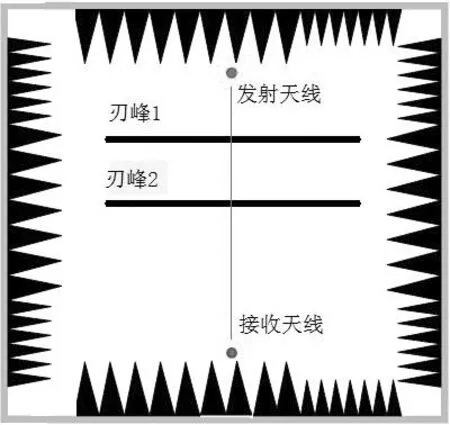
图1 实验平台构建

在单刃峰绕射问题中，为了得到可以和二维抛物方程比较的计算结果，使用高度为6.5cm的金属条作为刃峰1。刃峰1距离发射天线的距离为30cm，其宽度取的足够长，以避免从侧边方向过来的绕射波。图2 给出了单刃峰绕射的二维抛物方程法差分计算的结果和实验结果的对比。从实验结果可以看到，实验结果与抛物方程的仿真结果基本一致。图3所示是双刃峰绕射问题的抛物方程差分法的计算结果和实验结果的对比。在双刃峰绕射问题中，在刃峰1的基础上增加了刃峰2。刃峰2的高度为4.9cm，其宽度也取得足够长，以避免从侧方向传过的绕射波。由图2和图3可以看出，二维抛物方程差分法的计算结果同实验结果具有相同的变化规律。其中抛物方程法的计算结果略小于实验结果，主要是相关近似造成的。

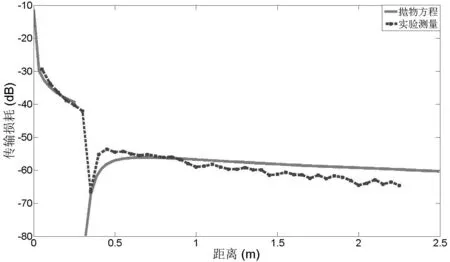
图2 单刃型障碍物的抛物方程计算与实验比较

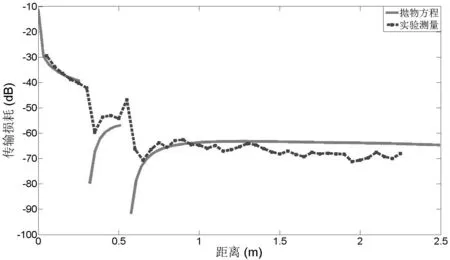
图3 双刃型障碍物的抛物方程计算与实验比较

4 结论

抛物方程差分法的求解是一种步进迭代的算法，每次计算一步便可以得到该步进上的场分布，再加上抛物方程本身包含电波传播所表现的绕射和折射效应，不需要再去专门考虑在传播路径上所产生的各种不同的传播机理，因此具有计算过程简单和计算精度高等优点。本文通过差分近似，得到了二维抛物方程的矩阵表示形式。通过对单刃峰和双刃峰绕射问题的数值计算和实验测量，验证二维抛物方程的差分求解的有效性，表明了该方法可以用于复杂环境中的电波传播预测。

[1]RecommendationITU-RP1546-5.Methodforpoint-to-areapredictionsforterrestrialservicesinthefrequencyrange30MHzto3000MHz[R].2013.

[2]MHata.Empiricalformulaforpropagationlossinlandmobileradioservices[J].IEEETransactionsonVehicularTechnology，317-325，September，1981.

[3]TSRappaport.WirelessCommunications[M].PearsonEducation，150-154，SecondEdition.

[4]胡绘斌.预测复杂环境下电波传播特性的算法研究[D].国防科技大学，2006.

[5]LeontovichMA，FockVA.SolutionofpropagationofelectromagneticwavesalongtheEarths’surfacebythemethodofparabolicequations[J].JPhysUSSR，1946，10(1)：13-23.

[6]KuttlerJR，DockeryGD.Theoreticaldescriptionoftheparabolicapproximation/Fouriersplit-stepmethodofrepresentingelectromagneticpropagationinthetroposphere[J].RadioScience，1991，26(2)：381-393.

[7]任明.电波传播损耗预测抛物型方程模拟[D].杭州电子科技大学，2012.

(责任编辑：宋金宝)

The Radio Wave Propagation Prediction Using Two Dimensional Parabolic Equation Based on Finite Difference Method

WANG Rui-dong，LU Gui-zhen

(Information Engineering School，Communication University of China，Beijing 100024，China)

The parabolic equation(PE)is a computational method for radio wave propagation loss besides the full wave method and ray tracing method.It has the capability to compute large range radio wave propagation problem and high computational accuracy.In this paper，we introduced the two dimensional PE firstly，and then we adopted finite difference method to approximate the PE.By doing this，we obtained the matrix equation which can be solved numerically.To verify this method，the classic single knife-edge and double knife-edge diffraction problems were computed.To investigate the validity of the computation results，we built the indoor scaling experiment environment to measure the propagation loss.It was found that the computational results and the measurement data are basically identical.

radio wave propagation；parabolic equation；finite difference method

2016-09-22

王瑞东(1987-)，男(汉族)，宁夏人，中国传媒大学博士研究生，E-mail：123495518@qq.com.

TN92

A

1673-4793(2017)01-0027-04