预测控制在电力电子技术中的应用
王利华++周荣富++吴鹏松


摘要:模型预测控制算法采用了多步预测、滚动优化和反馈校正等控制策略,因而具有控制效果好、鲁棒性强、对模型精确性要求不高,它和非线性预测控制比较有各自的优缺点,本文就它们如何在电力电子中的应用做了系统的分析和阐述,其优越的性能在工业控制中已经得到了广泛的应用,最后对预测控制在电力电子中的应用前景做出了展望。
关键词:模型预测控制 非线性预测控制 电力电子 自动控制
中图分类号:TM76 文献标识码:A 文章编号:1007-9416(2016)10-0004-04
电力电子技术是一门交叉学科,自动控制技术是电力电子设备的灵魂,它决定着系统的各种性能,如稳态精度、暂态响应速度、鲁棒性、可靠性等等。目前,许多控制方法都在电力电子领域得到了的应用,而一部分方法尚未得到大规模的研究和应用。预测控制是1978年由Richalet[1]提出的,经过近三十年的发展,已经形成三大公认的预测控制方法机理,即模型预测、滚动优化和反馈校正。预测控制由于其优越的性能在工业控制中得到应用,但在电力电子这样的快速系统的应用研究还处于起步阶段。本文对预测控制在电力电子中的应用研究做了小结,以期对这方面的研究起到促进作用。需要说明的是,有些电力电子方面文献[2]-[4]也以预测控制作为题目或关键词,但其所指的是无差拍控制等信号预测技术,和本文提到的预测控制应加以区别。
1 模型预测控制原理和应用
模型预测控制(Model Predictive Control,MPC)[5]是20世纪80年代发展起来的新型计算机控制算法,该算法直接产生于工业过程控制的实际应用,并不断完善和发展。模型预测控制算法采用了多步预测、滚动优化和反馈校正等控制策略,因而具有控制效果好、鲁棒性强、对模型精确性要求不高的优点。在工业生产过程中,许多对象都具有非线性、不确定、时变的特点,要建立精确的解析模型十分困难,因此传统的控制方法,如PID控制,难以获得良好的控制效果,而模型预测控制能够有效地用于复杂对象的控制。传统的预测控制采用基于脉冲响应的非参数模型作为内部模型,用过去和未来的输入输出信息,预测系统未来的输出状态,经过用实测系统输出与预测模型输出的误差来进行反馈校正,再与参考输入轨迹进行比较,通过二次型性能指标进行动态优化,计算当前时刻加于系统的控制动作,即先控制后动作,所以具有预见性,优于先有信息反馈,再有控制动作的经典反馈系统。
模型预测控制大多应用于工业过程控制领域,在要求快速响应的电力电子领域应用不多,原因在于快速系统要求控制算法的周期必须限制在很短的时间内,而传统的模型预测控制算法较复杂,运算量大,为此必须進行适当的改进。
1.1 以一阶差分方程作为预测模型
在传统预测控制中的滚动优化环节中,控制增量的最优化准则为:
其中y为系统输出,w为期望输出序列,λ为加权系数,△u是控制增量。预测控制以最优化准则的值最小化来确定控制增量△u。而且为了提高系统的鲁棒性,控制的目的不是使输出直接跟踪给定值,而是跟踪参考轨线,这样使快速性降低。
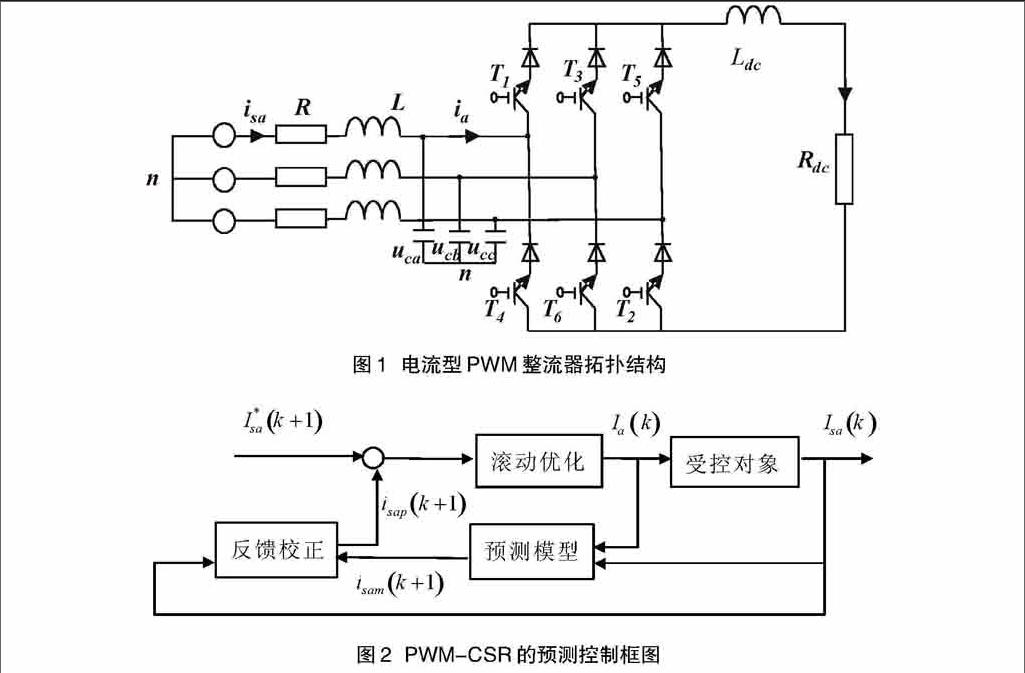
为了提高控制系统的快速性,文献[6][7]尝试将改进的预测控制应用于电流型PWM整流器(PWM Current Source Rectifier, PWM~CSR),电流型整流器的拓扑结构如图1所示。T1~T6构成三相变流器,其直流侧为大电感Ldc加负载电阻Rdc,交流侧通过电感L和电网连接,控制的目的是使网侧电压和电流同相且电流无畸变,功率因数接近于1。
首先,通过对系统方程的分析发现控制ia就能控制isa,为了简化预测模型,在PWM-CSR中,合理设计交流侧滤波器参数,使,则Ia(s)和Isa(s)间的传递函数为:
而文献[7]省略了参考轨迹。在反馈校正环节中,用实测系统输出isa(k)与预测模型输出isam(k)的误差来进行反馈校正,作为k+1时刻系统的闭环预测输出,即:
在动态优化过程中,即希望未来时刻的预测电流isap(k+1)尽可能地接近k+1时刻的给定值,又不希望控制量过大,所以优化性能指标选为:
系统的控制框图如图2所示。仿真和实验结果表明这种简化的模型预测控制不但具有传统预测控制的优点,又简化了算法,非常适合于快速系统,应用前景广阔。
1.2 模糊模型预测控制
虽然非线性预测控制可以改善电力电子系统的响应和控制精度,但前提条件是必须知道系统的精确模型,这在很多时候是做不到的。而模糊模型预测控制(Fuzzy Model Predictive Control)[8]无需系统结构和参数的先验知识,被当作是设计复杂控制系统的有效工具。T-S模糊模型适于一大类非线性系统的建模,所以可用来预测有源电力滤波器的谐波电流。在模糊建模过程中,模糊模型来自于测量得到的输入、输出数据,建模的方法是模糊聚类,产生了模糊集合后就可用来进行预测控制了。模糊预测控制用于APF的系统框图如图3所示。测量得到的输入、输出数据为APF输出的补偿电流和控制矢量的当前值和过去若干时刻的值,经模糊模型预测算法后,得到控制矢量u。
模糊建模的过程是这样的,首先APF输出补偿电流可表达为:
式中是归一划的第i个规则的真值。
为了使模型更加简洁和准确,还需进行模糊模型辨识,包括以下4个步骤:(1)用模糊聚类方法得到模糊前提条件;(2)检查和合并相近模糊集;(3)用最小平方参数评价的方法确定规则推理;(4)确定模糊基的合适数量。
接下来的就可以设计预测控制系统,定义目标函数为:
式中是补偿电流参考值,Hc是控制范围,Hp是预测范围,P和Q是确定的权矩阵。此外,为了避免在每个采样周期都要解决这种非凸的优化问题,使预测控制不适合于快速系统,采用了分支和界定(branch-and-bound)的优化方法。

