一种改进的飞行器动弯矩识别方法
周昊天,于开平
(哈尔滨工业大学航天学院,哈尔滨150001)
一种改进的飞行器动弯矩识别方法
周昊天,于开平
(哈尔滨工业大学航天学院,哈尔滨150001)
提出一种改进的飞行器动弯矩识别方法,该方法引入了频域积分算法,避免了时域方法中消除趋势项以及滤波所带来的问题。对加速度响应进行两次积分得到结构弹性位移响应,然后根据模态叠加理论求解出广义坐标,最后结合模态弯矩识别截面的动弯矩响应。通过悬臂梁试验验证了算法的有效性,并与传统方法识别出的结果进行对比。结果表明,新方法的识别结果更接近试验实测动弯矩响应,具有更高的精度。最后将该方法应用于某型号飞行器,并给出了识别结果。
模态叠加法; 弯矩识别;频域积分
0 引 言
火箭等飞行器在飞行过程中会受到复杂外力的作用。在这些外力的作用下,飞行器结构会产生动响应。为了使火箭等飞行器在飞行阶段能够平稳安全地运行,通常需要对结构各舱段的设计提出一定要求,比如强度、刚度、稳定性等。为了提出准确的指标要求,通常需要建立完整的飞行器结构动力学模型,在一定的初始条件和外力作用下进行仿真模拟,计算出结构各舱段的响应,而后可以根据响应得到各截面的弯矩、剪力等信息。然而在实际运行过程中,火箭等飞行器结构受到复杂外力作用,完全模拟复杂工况非常困难,因此通过已有的飞行或试验数据进行内力识别可以作为重要的参考。
对于飞行器设计而言,内力的大小与分布是关系到飞行器能否达到设计目标的重要参数。飞行器在飞行过程中无法直接测量内力响应,虽然可以通过仿真的方法模拟飞行器受力情况计算出结构的动态内力响应,然而飞行器飞行过程中所受外力亦无法实测,同时飞行器实际工况复杂无法完全模拟,因此,出现了一些利用结构响应进行内力识别的方法。
当前国内外已经针对内力识别问题开展了一些研究,传统方法采用结构的应变响应计算得到动弯矩[5],这类方法通常容易受到飞行器结构的限制[6]。另外一些方法采用位移响应计算得到动内力。例如,龙源等[7]利用小波分析在时频域都具有表征信号局部特征的特点,提出了一种识别固体火箭截面剪力和弯矩的方法;之后又对原方法做了很大改进,并对一固体火箭关键截面弯矩做了识别[4]。纪跃波等[8]根据虚功原理通过测量结构的位移响应,给出了与边界条件无关的地下隧道内力识别结果。
飞行器在飞行过程中的位移响应无法直接测得,通常做法是在时域利用加速度响应进行二次积分获得位移响应。然而在时域进行积分需要预先对数据进行滤波处理,在积分过程中会不可避免地引入趋势项[4],并且消除趋势项本身也需要细致而复杂的调整过程。本文引入了加速度频域积分方法,避免了原时域方法中选择小波基函数以及小波分解层数等复杂过程,通过悬臂梁试验验证了本方法具有较高的识别精度,在工程应用中具备一定的实用价值。
1 截面弯矩识别的理论基础
在工程实际中常把飞行器模型简化为多自由度系统,再参照结构动力学中的模态叠加理论,认为几何位移可以由n阶广义位移叠加而成:
(1)
式中:x(t)为测量点位置的几何位移,ur为该点处第r阶振型,qr(t)为第r阶广义坐标。从式(1)可以看出,若已知m(m>r)个测点处的几何位移以及对应点处的前r阶振型分量,则可以通过最小二乘方法计算出前r阶的广义坐标。另外可以通过理论计算或有限元等方法获得对应点处各阶模态弯矩及剪力,结合求得的广义坐标,可以进行截面内力的识别:
(2)
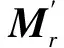
2 改进的截面弯矩识别方法
由第1节的理论可知,只要获得飞行器的弹性位移响应,再结合理论推导或者仿真计算得出模态信息,即可进行结构动弯矩的识别工作。一般情况下很难直接测量飞行器的弹性位移响应,但可以利用测量到的加速度响应进行两次积分获得。对加速度响应积分一般采用时域积分方法,例如采用梯形公式。时域积分方法在积分过程中需要对数据进行消除趋势项及滤波处理,否则无法获得弹性位移,如图1所示。
在实际应用中,常采用小波[9]或者经验模态分解[7](Empiricalmodedecomposition,EMD)[10]作为消除趋势项的手段,但无论是小波还是EMD方法都容易出现边界效应[11],使数据失真,如图2所示。
鉴于内力识别仅需要弹性位移,这里考虑引入频域积分方法[12]。频域积分通过傅里叶变换将时域信号转换到频域上而后进行积分。
考虑一个离散时间加速度序列a(n),其长度为N,对其进行离散傅里叶变换可以得到:
(3)
式中:a(k)为变换后的复数序列,f(k)为对应频率,fs为采样频率。a(k)对应的简谐波可以写成如下形式:
a(t)k=Akcos(ωkt+φk)
(4)
其中,
(5)
对式(4)进行两次积分,可得对应频率下的位移谐波如下:
S(t)k=Askcos(ωskt+φsk)
(6)
其中,
(7)
因此,积分得到的位移表达式为:
(8)
如用F(x)表示傅里叶变换,用F-1(x)表示傅里叶逆变换,式(8)可以记为:
(9)
由式(9)可知,在频域积分过程中,频率小于1Hz的加速度谐波中的误差被放大,同时考虑到需要消除刚体位移,需要对积分过程加以控制。本文采用的方法是低频截止方法[13],选定一个特定频率fT,低于该频率的加速度信号幅值置零。通过低频截止处理可以有效避免低频部分加速度信号误差的放大效应,同时消除积分后的刚体位移。fT的选择与加速度传感器的频率下限相关,一般应大于传感器频率下限。
3 试验验证与分析
在航天工程中,为了简化计算,常采用梁模型代替全尺寸的飞行器模型,为了验证算法的有效性,这里以悬臂梁为对象进行试验研究。
悬臂钢梁总长1200mm,宽50mm,厚9mm,五个加速度传感器分别布置在距悬臂梁根部26、37、55、84、120cm的位置上,应变片位置距悬臂梁根部5cm,上下对称布置,构成半桥测量结构,试验装置如图3所示。
为了与飞行状态下的飞行器工况相契合,这里采用宽频的白噪声进行激励,利用采集到的加速度信号与仿真计算得到的悬臂梁振型、模态弯矩进行内力识别。
根据式(9)对加速度信号进行积分得到弹性位移响应如图4所示,而后根据式(1)可得各阶弹性广义位移,如图5所示。
一般而言,对于宽频激励下的结构响应,低阶广义位移贡献较大而高阶则趋向减少。对式(2),根据经验取前三阶广义位移进行内力识别即可得到较为理想的结果,为了与实测弯矩响应对比,这里对应变片位置处的弯矩进行识别,如图6所示。从图6可以看出,本文提出的频域积分方法的识别结果与试验实测结果相位一致,同时趋势吻合程度较好,结果表明该方法可行且有效。
此外,与时域积分方法得到的结果相比,频域积分方法的识别结果更接近实测值,见图7。试验结果表明,与时域积分方法相比,本文提出的频域积分方法具有更高的识别精度。
在获得各阶弹性位移后,如果同样已知其他任意截面处的模态弯矩则可以对该任意截面进行内力识别,图8为距悬臂梁根部10cm处的动弯矩识别结果。
对于飞行器设计,关键截面处的最大载荷(内力)响应更值得关注。对飞行遥测数据进行处理,得到了飞行器飞行过程中的内力响应,如图9所示。从图9可以看出,该关键截面处的最大动弯矩发生在0.22s时刻,而设计人员预估最大值发生在0.2s左右,最大值绝对值为1.02左右,经比较两者相对误差小于5%,说明本方法可以为飞行器设计人员提供很好的参考与帮助。
4 结 论
对于无法直接测量的飞行器内力响应,本文给出了一种基于加速度频域积分的识别方法,该方法避免了传统时域积分方法中需要滤波以及消除趋势项的步骤。本文通过悬臂梁试验验证了算法的有效性。试验结果表明,与时域积分方法相比,本文提出的改进方法的识别结果与实测值更接近,具有更高的识别精度。最后,利用某型号飞行器遥测数据进行了动弯矩识别,改进方法识别出的最大动弯矩与设计人员预估的最大动弯矩非常接近。本文提出的改进方法对飞行器载荷设计与评估有重要的参考意义。
[1] 马斌捷, 洪良友, 王国庆, 等. 火箭动态弯矩测量的频响特性分析[J]. 强度与环境, 2012, 39(5): 1-6. [MaBin-jie,HongLiang-you,WangGuo-qing,etal.Frequencyresponsecharacteristicanalysisofthemeasurementaboutdynamicbendingmomentforlaunchvehicles[J].Structure&EnvironmentEngineering, 2012, 39(5): 1-6.]
[2] 洪良友, 马斌捷, 贾亮, 等. 火箭结构动态载荷响应的非正交测点测量方法[J]. 导弹与航天运载技术, 2015,(4): 90-94. [HongLiang-you,MaBin-jie,JiaLiang,etal.Researchonthetechnologyofdynamicloadmeasurementusingnon-orthogonalmeasurepointsforlaunchvehicle[J].MissilesandSpaceVehicles, 2015,(4): 90-94.]
[3] 尹云玉. 固体火箭横向响应载荷识别方法[J]. 宇航学报, 2009, 30(6): 2135-2139.[YinYun-yu.Theidentificationmethodoftransverserespondingloadforsolidrocket[J].JournalofAstronautics,2009, 30(6): 2135-2139.]
[4] 尹云玉. 固体火箭自由运行状态截面弯矩识别方法[J]. 宇航学报, 2010, 31(7): 1706-1710. [YinYun-yu.Anidentificationmethodfortransverseresponsemomentofsolidrocketduringfreeflightstate[J].JournalofAstronautics, 2010, 31(7): 1706-1710.]
[5]FuentesR.Internalforcesofundergroundstructuresfromobserveddisplacements[J].TunnellingandUndergroundSpaceTechnology, 2015, 49: 50-66.
[6] 周哲, 庄良杰, 熊正南, 等. 基于小波分析的陀螺漂移趋势项提取[J]. 中国惯性技术学报, 1999,7(4): 59-61.[ZhouZhe,ZhuangLiang-jie,XiongZheng-nan,etal.TrendextractionofGyro'sdriftbasedonwaveletanalysis[J].JournalofChineseInertialTechnology, 1999,7(4): 59-61.]
[7] 龙源, 谢全民, 钟明寿, 等. 爆破震动测试信号预处理分析中趋势项去除方法研究[J]. 工程力学, 2012, 29(10): 63-68. [LongYuan,XieQuan-min,ZhongMing-shou,etal.Researchontrendremovingmethodsinpreprocessinganalysisblastingvibrationmonitoringsignals[J].EngineeringMechanics, 2012, 29(10): 63-68.]
[8] 纪跃波, 秦树人, 柏林, 等. 有限区间信号边界效应问题的研究[J]. 振动与冲击, 2002, 21(4): 108-111. [JiYue-bo,QinShu-ren,BaiLin,etal.Researchontheedgeeffectofcutoffsignalwithlimitedtimedomain[J].JournalofVibrationandShock, 2002, 21(4): 108-111.]
[9] 徐庆华. 试采用FFT方法实现加速度、速度与位移的相互转换[J]. 振动、测试与诊断, 1997, 17(4): 30-34. [XuQing-hua.Conversionbetweenvibrationalacceleration,velocityanddisplacementusingFFT[J].JournalofVibration,Measurement&Diagnosis, 1997, 17(4): 30-34.]
[10] 蒋良潍, 姚令侃, 吴伟. 边坡振动台模型实验动位移的加速度时程积分探讨[J]. 防灾减灾工程学报, 2009, 29(3): 261-266. [JiangLiang-wei,YaoLing-kan,WuWei.Studyoncalculationofdynamicdisplacementfromtimeintegrationofaccelerationinshakingtablemodeltestsofsideslope[J].JournalofDisasterPreventionandMitigationEngineering, 2009, 29(3): 261-266.]
通信地址:哈尔滨工业大学344信箱(150001)
电话:(0451)86414320
E-mail:szzhouhaotian@126.com
于开平(1968-),男,博士,教授,主要从事结构动力学研究。本文通信作者。
通信地址:哈尔滨工业大学344信箱(150001)
电话:(0451)86414320
E-mail:yukp@hit.edu.cn
(编辑:牛苗苗)
An Improved Identification Method for Dynamic Bending Moment Responses of Flight Vehicles
ZHOU Hao-tian, YU Kai-ping
(School of Astronautics, Harbin Institute of Technology, Harbin 150001,China)
An improved identification method based on the mode superposition method for dynamic bending moment responses of flight vehicles is proposed in this paper. A frequency domain integration algorithm is introduced to avoid the problems caused by the tendency eliminating and signal filtering when using the time-domain integration method. Firstly, the displacement response of the flight vehicle is obtained by integrating the acceleration responses twice. Then, the generalized displacement is calculated by the mode superposition method. Finally, the dynamic bending moment response is identified by utilizing the modal moment. The validity of this approach is verified through an experiment on a cantilever beam, where the results identified by using both the time-domain integration and frequency-domain integration method are presented. It is demonstrated that the results obtained by the improved method are closer to the real moments than that obtained by the classical time-domain method, namely the improved method has a higher accuracy. Furthermore, the proposed method is applied to estimate the dynamic bending moment responses of a vehicle during the flight, and the results are given.
Mode superposition method; Response moment identification;Frequency-domain integration
2016-09-13;
2016-12-15
国家自然科学基金(11372084)
V421
A
1000-1328(2017)03-0248-05
10.3873/j.issn.1000-1328.2017.03.004
周昊天(1989-),男,博士生,主要从事结构动力学反问题研究。

