砂土中地下粮食圆形筒仓抗浮模拟实验研究

张会军，刘海燕，张庆章

（1．河南金地集团祥运置业有限公司，河南郑州 450047；2．河南工业大学土木建筑学院，河南郑州 450001）

砂土中地下粮食圆形筒仓抗浮模拟实验研究

张会军1，刘海燕2，张庆章2

（1．河南金地集团祥运置业有限公司，河南郑州 450047；2．河南工业大学土木建筑学院，河南郑州 450001）

目前有关地下大体积结构抗浮设计尚未形成完整的理论体系，地下粮食圆形筒仓设计者们往往采用不考虑土体对筒仓抗浮的有利作用，较为保守地进行设计。基于此，通过理论分析，考虑地下粮食圆形筒仓仓壁与土体的摩擦作用、仓底与土体之间的粘结力及仓底可能存在的负压作用等多种对抗浮设计有利的因素，采用室内模型模拟的方法，获得在密实粗砂土质中综合折减系数为0．40～0．45，采用数学分析求得浮力折减系数为0．94，基于阿基米德原理计算结构抗浮时，考虑土体对仓体有利作用，安全系数可调整为0．52，不考虑土体对仓体有利作用，安全系数可调整为0．99。

地下粮仓；抗浮；土体作用；折减系数

目前，我国的粮仓主导仓型仍以高大平房仓和大直径筒仓为主，且多数建造于地表以上，致使储粮环境并不理想，尤其在夏季，仓内温度常达35℃以上，为防止粮食虫蛀、霉变等情况的发生，需对粮食进行化学药剂熏蒸和采用人工制冷的方法对粮食进行冷却［1］，这势必会在对粮食造成污染的同时耗费大量的能源，不符合国家所倡导的构建节约型社会的要求，不利于社会的可持续发展。

地下粮仓以其良好的隐蔽、避光及密闭低温等优点，成为实现粮食绿色储粮的理想仓型，已引起粮食仓储行业工作者们的关注。伴随新型地下粮仓向高水位等复杂地质条件地区的推广，仓体将受到较大的地下水的作用，然而目前地下结构水浮力计算理论尚不成熟，地下粮仓所涉及的浮力计算问题也开始困扰粮食仓储设计者。粮仓作为特种结构，所受地下水浮力的专项研究更为欠缺，亟待进一步探索。

本课题基于目前国内外不同的专家学者对地下结构所受浮力不同研究及相关结论，基于地下结构在受地下水浮力作用时，结构本身与土体相接触的事实，结合地下粮仓不同于一般地下结构的实际情况，探究当采用阿基米德原理计算浮力时是否应对计算公式进行折减及折减系数如何取值，为地下结构尤其是地下粮仓抗浮设计时提供一定的借鉴。

1 材料与方法

参照在建地下粮食圆形筒仓的结构设计、场地条件、施工情况等因素，结合模型实验理论，忽略次要因素、突出重点，在实验室的条件下发挥其优势进行模型实验。

1．1 实验设计思路

根据梅国雄、李广信等学者［2－4］研究分析，推测当地下粮食圆形筒仓受到地下水浮力作用时，仓体结构可能受到与浮力方向相反作用力，包括仓体四周土体的摩擦力、仓底与土体的粘结力以及仓体底部所产生的负压空间所形成的负压力等。

本次实验即为探究在静水条件下，地下粮食圆形筒仓受到地下水浮力作用时，上述各与浮力方向相反的作用力所占浮力的比重，求得地下圆形粮食筒仓的抗浮折减系数，进而对常规浮力计算公式进行修正模型在土中受力示意，见图1：

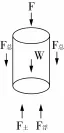
图1 模型置于地基土中时受力示意图

图中：

F－实验装置提供的约束反力；

W－模型自重及其它自由置于模型上的仪器等；

F土－仓底土体对模型的支承力；

F浮－模型所受浮力；

F总－仓壁四周土体对仓体的作用力，包括摩擦力、粘结力、负压力等。

向模型池中缓慢注水，伴随“地下水位”的上升，“粮食筒仓”受浮力作用逐渐产生上浮趋势，F浮的值开始由零逐渐变大直至模型发生上浮。其中，上浮临界点通过位移传感器及压力传感器监测确定。

“粮食筒仓”尚未发生上浮时，根据受力平衡则有：

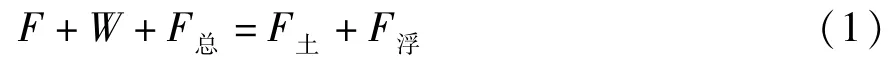
“粮食筒仓”发生上浮，F土＝0，根据受力平衡则有：

通过实验求得有利于抗浮作用的综合值F总，进而计算出F总占F浮的比值，求得浮力综合折减系数ε0：

再根据数学分析求得浮力折减系数ε0。

1．2 实验模型与装置

1．2．1 实验模型

为了更接近实际地下粮食圆形筒仓所处的工作环境，模拟地基土体的盛装容器应尽可能的大些，消除盛装容器对土体约束而对“粮食筒仓”模型产生影响，同时盛装容器应有足够强度满足实验的要求，故选用厚度为10 mm钢化玻璃用玻璃胶拼装成2 000 mm（长）×2 000 mm（宽）×1 00 0mm（高）的方形池，并用3 mm×3 mm的矩形不锈钢对其进行加固，见图2。

图2 方形池

“地下粮食圆形筒仓”模型的选用需要具有足够的刚度，还需考虑模型的重量，避免由于模型过重使得在其受到浮力作用时上浮幅度较小甚至完全不能上浮。经计算，最终选定厚度为2 mm的钢板加工制作成直径分别为400、500和600 mm，深度均为700 mm的圆筒，分别依次标记为A、B、C，圆筒外侧涂抹水泥砂浆使其与接近实际仓体材料，模型见图3。

图3 “粮食圆形筒仓”模型

1．2．2 测量系统

根据测量对象的不同可将测量系统分为水位测量装置、荷载测量装置以及信息采集系统等。

为避免土壤毛细现象的影响，水位测量采用连通器原理，分别在方形池对角设置透明管观测并用钢尺进行测量；利用位移传感器对“粮食筒仓”模型的上浮位移进行监测，为确定结构上浮临界点提供依据；荷载测量包括称量“筒仓模型”重量的精度为0．005 kg的电子秤及用于测量筒仓模型上浮时所受的约束反力F的S型拉压传感器；信息采集系统有计算机、电源／控制器、数据采集器等，见图4。

图4 数据采集系统连接方式

1．3 实验方法

采用水洗砂作为基体，分别将模型A、B、C埋置于基体中，测定其受到“地下水”浮力作用时，基体土对“仓体”的影响情况。

1．3．1 砂土中实验步骤

在无黏性土中进行土体作用实验时，依次对模型A、B、C进行实验，具体操作步骤如下：

1）分别在“粮食筒仓”模型A、B、C的“仓壁”外侧涂抹水泥砂浆，并养护一周；

2）往模型池中填放沙土至距离模型池底部约15 cm厚，并对其进行压实；

3）将模型放置在已经过压实的沙土之上并位于装置的中间位置，调节安装在反力横梁上的竖向位置调节装置，高度适中以便安装压力传感器及位移传感器；

4）继续往模型池中填放沙土，每隔10 cm左右进行压实，直至沙土高度距离模型池底部约70 cm，如图5；

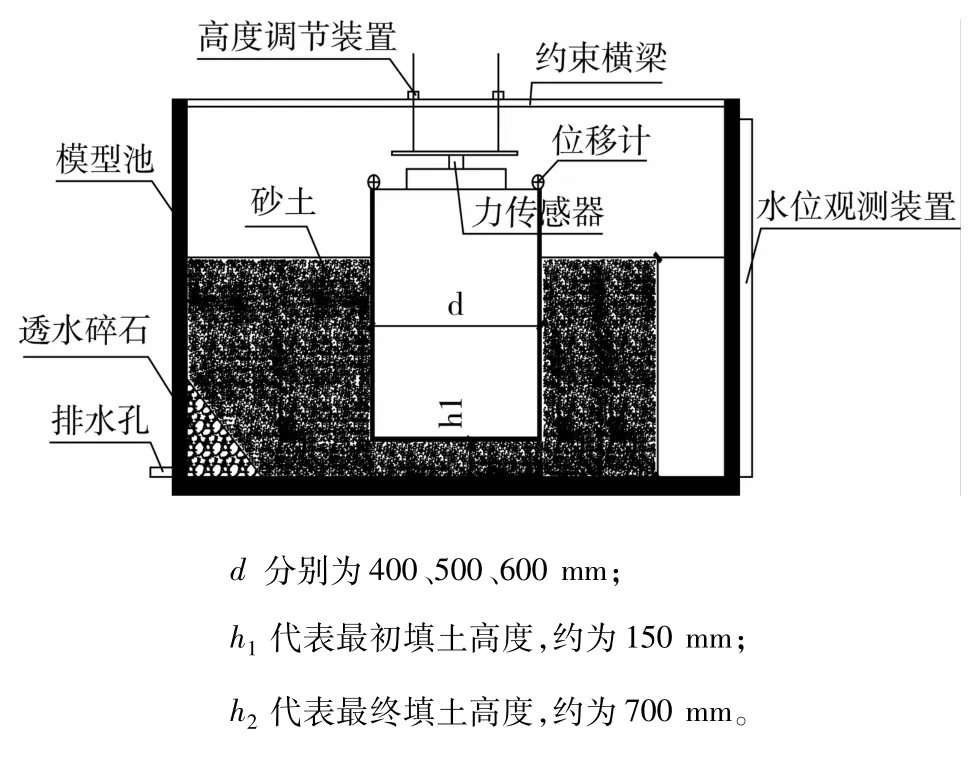
图5 模型示意图

5）安装位移传感器，并将压力传感器水平正向放置在地面上；

6）启动静态应变测试分析系统，对压力传感器和位移传感器进行测点平衡，继而安装压力传感器，如图6。

图6 砂土中实验

7）缓慢向模型池内注水，观测水位及压力与位移变化，每隔10 mm进行一次读数，当计算机显示压力及位移标示线发生变化时减小读数间隔时间；

8）对实验数据进行整理分析。

2 结果与分析

2．1 砂土中实验结果

模型外侧涂抹有水泥砂浆，周长和质量测定结果见表1。

表1 模型周长及质量（含水泥砂浆）

缓慢向模型池中注水，分别对模型A、B、C进行实验，实验结果见图7、图8及图9。图中土体作用力F总由支反力F、模型自重、计算浮力F浮等数值推算而得，故当模型所受浮力小于模型重量时，土体作用力数值为零。

由图可看出，随着往模型池中缓慢注水，水位在不断增加，筒仓模型所受到的浮力也随之相应增加，但计算所得筒仓模型所受的摩擦力当增加到一定数值时则开始下降，表明此时筒仓模型已经受水浮力作用开始显著上移，由位移计检测的结果也能进一步佐证，该点数值可以作为模型上浮破坏点的取值，可以以此进一步计算筒仓受水浮力作用发生上浮时所受土体作用占其所受浮力的比重，求得综合折减系数，计算结果见表2。

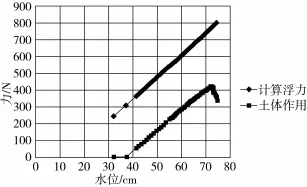
图7 模型A在砂土中实验结果图

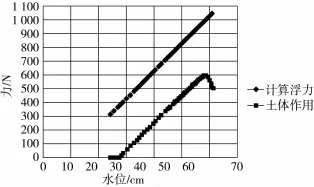
图8 模型B在砂土中实验结果图

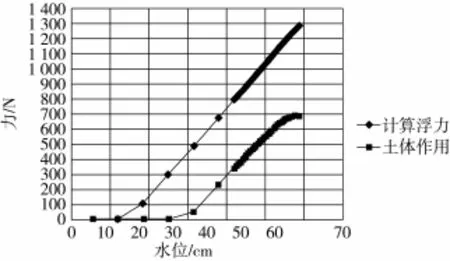
图9 模型C在砂土中实验结果图

表2 砂土中实验数据汇总

2．2 砂土试样采集与分析

2．2．1 颗粒分析实验结果

根据《建筑用砂》（GB14684—2011）［5］要求，筛分法对砂子进行颗粒分析。筛分结果见表3。

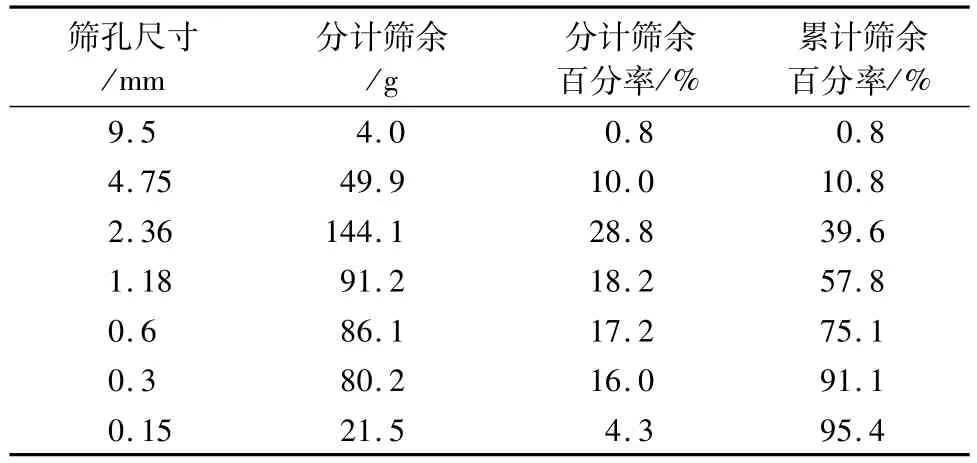
表3 砂子筛分结果

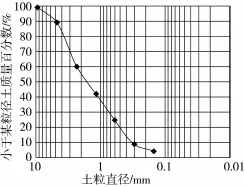
图10 颗粒级配曲线图

计算得砂的细度模数为Mx＝3．42，属于粗砂。同时，绘制砂子的颗粒级配曲线见图10，级配良好。

2．2．2 砂的相对密实度实验结果

本实验所采用的粗砂为水洗砂，根据《土工实验方法标准》（GB／T 50123—1999）［6］原位密度实验要求，选取灌水法计算所采原状土体积，继而对所采集的土样进行烘干，计算土样的原位干密度，再采用漏斗法和振动法分别计算出土样的最小干密度和最大干密度，进一步计算出其相应的相对密度。

分别对模型A、B、C实验后的原位土进行采样与测定，测定结果见表4。

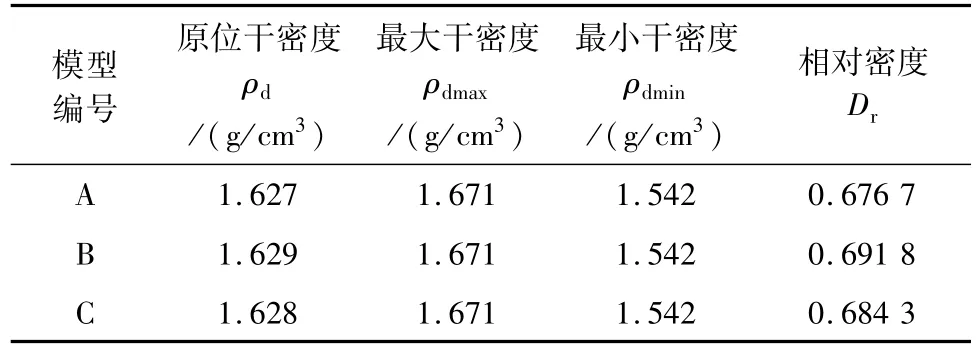
表4 砂土相对密实实验结果

可以判定实验过程中，砂土密实度为密实。

2．3 结果分析

根据三个不同直径“粮食筒仓”模型实验结构，经初步分析得浮力综合折减系数的范围为0．40～

0．45，该折减系数为综合折减系数，计算过程中包含多种有利于抗浮的因素，主要有地下粮仓仓壁与地下土的摩擦力f、仓底与土体产生的有利于抗浮作用的力c，即有F总＝f＋c，从而得出：

根据各作用力的特点进行分析，进而得到各作用力的表达式：

式中：

ε－土中水浮力的折减系数；

ρ－地下水密度；

g－重力加速度；

H－粮仓模型埋置于水面下的深度；

L－地下粮仓模型周长；

μ－粮仓模型仓壁与土体的摩擦系数；

k0－土的侧压力系数；

γ·－土的有效重度；

h－模型埋置于土下的深度；

φ－粮仓模型仓底与土体有利作用力系数；

S－粮仓模型仓底面积。

由（4）可知模型所受浮力与粮仓模型底面积S和粮仓模型埋置与水下的深度H的乘积成正比；由式（5）可知粮仓模型仓壁与土体的摩擦力与模型周长L和模型埋置于土下的深度h成正相关；由式（6）可知仓底与土体有利于抗浮作用力与模型仓底面积S成正比。故可将上述3式改写为：

将式（7）、式（8）及式（9）代入式（3），则有：

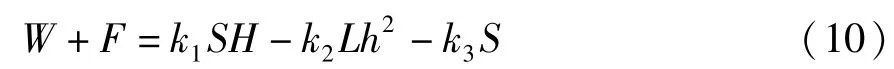
根据模型A、模型B和模型C在粗砂中的实验结果可得3个方程构成三元一次方程组：

求解得：

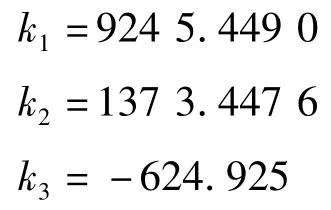
将k1＝7 213．920 919代入式k1＝ερg中，计算可得浮力折减系数为：

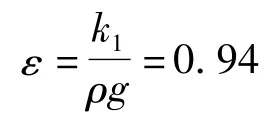
2．4 浮力计算公式修正

综合目前有关地下结构抗浮设计的规范如《建筑结构荷载规范》（GB 50009—2012）［7］、《地铁设计规范》（GB 50157—2003）［8］、《石油化工钢筋混凝土水池结构设计规范》（SH／T 3132—2002）［9］等的规定，在进行地下结构抗浮设计和稳定性验算时，在考虑地下结构四周土体对结构有利作用时，选取安全性系数为1．15，在不计入土体有利作用时，选取安全性系数为1．05。在计算地下水浮力时，除进行工程现场详细的地质勘测及有关实验，较多的工程仍旧采用基于阿基米德原理的计算方法，但考虑到饱和土密度、渗流等因素是否应对采用阿基米德原理计算所得的浮力进行折减，尚未形成一致意见。目前进行地下结构抗浮计算时，采用的计算公式为：

式中：

Gk－抗浮力标准值；

Fk－设计浮力标准值；

ρ－地下水的密度（kg／m3）；

g－重力加速度（N／kg）；

V－地下粮食筒仓的排卡水量（m3）；

η－安全系数。

2．4．1 计入土体有利作用

在考虑地下结构四周土体对结构有利作用时，公式（11）中的安全系数η可调整为：

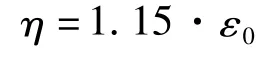
实验求得综合折减系数范围为0．40～0．45，详见表2，取综合折减系数为0．45，故可将式（11）调整为：

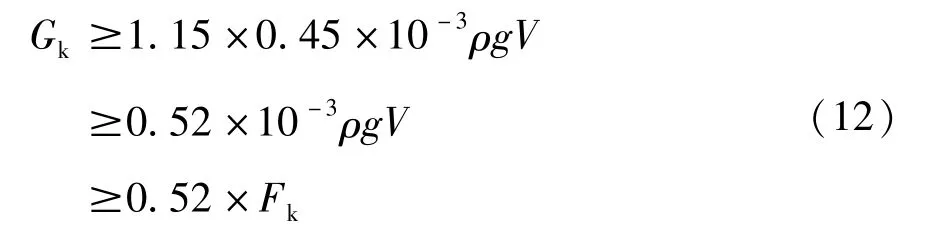
2．4．2 不计入土体有利作用

在不计入土体有利作用时，公式（11）中的安全系数η可调整为：

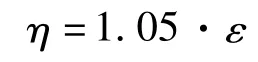
根据三组不同实验推导而得的浮力折减系数为0．94，在不计入土体作用时，故可将式（11）调整为：

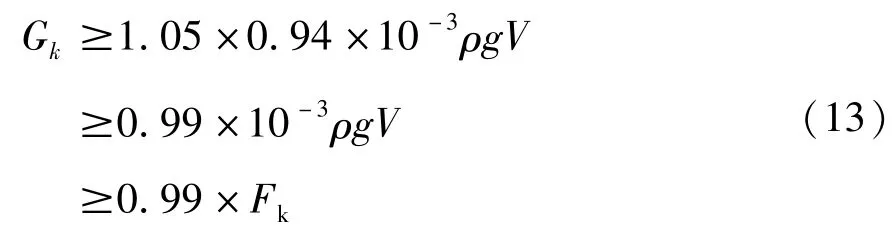
在计算地下粮食圆形筒抗浮计算时，可采取下列计算公式：

η—安全调整系数，可按表5取值。

表5 砂土中抗浮安全调整系数

3 结语

当地下粮食圆形筒仓受到水浮力作用时，筒仓会受到仓壁和四周土体摩擦作用，仓底也会受到粘结力、负压力等作用，同时，浮力水位的取值也往往受地下水体赋存情况、土质等因素影响，在地下粮食筒仓抗浮设计时笼统地采用阿基米德原理进行浮力计算，势必会造成资源浪费，同时加大施工难度。

通过采用尺寸不同的三组“粮食圆形筒仓”模型进行实验，综合多种有利于抗浮设计的因素求得在颗粒级配良好的密实粗砂土质中，浮力综合折减系数为0．40～0．45，并经数学分析求得浮力折减系数为0．94，在此基础上对地下粮食圆形筒仓基于阿基米德原理的抗浮计算公式进行调整，推算得出在计入土体对仓体的有利作用时，该安全调整系数为0．52，不考虑土体对仓体的有利作用，该安全调整系数为0．99，为实际工程进行浮力计算时提供借鉴。

［1］余汉华，王录民，王振清，等．我国地下粮仓的应用现状及前瞻［J］．河南工业大学学报（自然科学版），2008，29（6）：79－81．

［2］梅国雄，宋林辉，等．关于基础抗浮的若干问题探讨［J］．岩土工程学报，2008，30：238－242．

［3］李广信，吴剑敏．关于地下结构浮力计算的若干问题［J］．土工基础，2003，17（3）：39－41．

［4］丁晓龙，饱和介质中建筑基础浮力折减系数的试验测定方法［J］．基础及前沿研究，2007，7：267－268．

［5］GB 14684—2011，中华人民共和国国家标准．建筑用砂［S］．

［6］GB／T 50123—1999，中华人民共和国国家标准．土工试验方法标准［S］．

［7］GB 50009—2012，中华人民共和国国家标准．建筑结构荷载规范［S］．

［8］GB 50157—2013，中华人民共和国国家标准．地铁设计规范［S］．

［9］SH／T 3132—2002，中华人民共和国行业标准．石油化工钢筋混凝土水池结构设计规范［S］．

Simulation experiment of anti－floating of underground grain silos in sandy soil

ZHANG Hui－jun1，LIU Hai－yan2，ZHANG Qing－zhang2
（1．Xiangyun Real Estate Co．，Ltd．，Henan Jindi Group，Zhengzhou Henan 450047；2．Colllege of Civil Engineering and Architecture，Henan University of Technology，Zhengzhou Henan 450001）

At present，the complete system info about anti－floating design of the underground mass structure has not yet been formed，designers of underground circular grain silo often calculate it without considering the effect of the soil which is good for the silo anti－floating．Based on this，through theoretical analysis，considering the various factors which are good for anti－floating design，such as the wall friction with the soil function，cohesive force between silo bottom and soil，negative pressure possibly existing and so on，adopting the method of indoor simulation experiment，what can be got is that comprehensive reduction factor in dense sand soil can be adjusted to 0．40～0．45，using mathematical analysis for buoyancy reduction factor can be adjusted to 0．94，considering the favorable effect to warehouse of soil body，safety factor，which is based on anti－floating calculation structure on the basis of the principle of Archimedes，safety factor can be adjusted to 0．52，if not，it can be adjusted to 0．99．

underground grain silos；anti－floating；action of soil；reduction factor

TU 267＋．1

A

1007－7561（2017）02－0099－06

2016－09－28

国家粮食公益性行业科研专项（201413007－01）

张会军，1965年出生，男，高级工程师．

刘海燕，1979年出生，女，副教授，硕士生导师．