主成分分析法在数字图像压缩中的的应用

鲁书山++沈小林++樊凯强

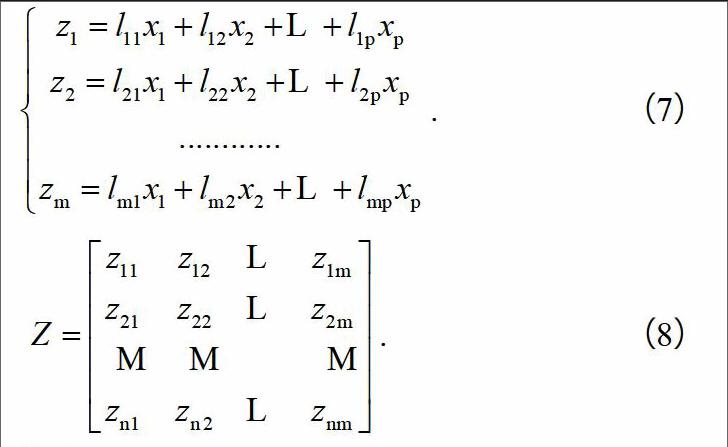
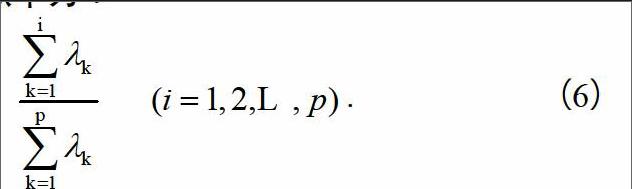
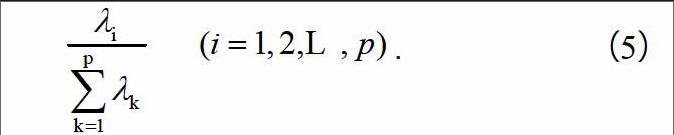
摘 要：阐述里主成分分析法的定义，及应用于实际的意义，通过matlab编程实现主成分分析法在图像压缩方面的应用，在编程过程中设置不同主成分个数来显示不同的处理结果。在对处理结果进行分析，同时也对主成分分析法的性质有了更直观的认识，方便日后在其他领域的应用。

关键词：主成分分析法；图像压缩；特征提取；matlab编程

中图分类号：TP309.7 文献标识码：A DOI：10.15913/j.cnki.kjycx.2016.23.098

主成分分析法是用降维的思想，用几个互不相关的主成分反映原始变量的大部分信息的统计方法。能有效降低数据维度，减少计算量，在涉及到数理统计的各个领域均有广泛的应用。本文先介绍主成分分析的原理，再通过matlab用主成分分析法对图像进行压缩，实现主成分在图像处理中的应用。

1 主成分分析法概念及性质

1.1 概念

假定有n个样本，每个样本由p个变量构成，则可以组成一个n×p阶的数据矩阵：

设x1，x2，…，xP为原变量，z1，z2，…，zm（m≤p）为新变量，则：

系数lij为新变量对原变量的反应情况。

1.2 性质

zi与zk（i≠k；i，k=1，2，…，m；j=1，2，…，p）相互无关；z1是x1，x2，…，xP的一切线性组合中方差最大者，z2是与z1不相关的x1，x2，…，xP的所有线性组合中方差最大者；zm是与z1，z2，……，zm-1都不相关的x1，x2，…xP的所有线性组合中方差最大者。则新变量指标z1，z2，…，zm分别称为原变量指标x1，x2，…，xP的第1，第2，…，第m主成分。

通过以上表述可知，主成分分析的实质是计算主成分zi（i=1，2，…，m）所反映的原变量xj（j=1，2，…，p）上的荷载 lij（i=1，2，…，m；j=1，2，…，p）。它们分别是相关矩阵（也就是x1，x2，…，xP 的相关系数矩阵）m个较大的特征值所对应的特征向量。

2 计算步骤

2.1 计算相关系数矩阵

相关系数矩阵为：

rij（i，j=1，2，…，p）为原变量xi与xj标准化后的相关系数，rij=rji，其计算公式为：

2.2 计算特征值与特征向量

解特征方程|λI-R|=0，求出特征值，并使其按大小顺序排列λ1≥λ2≥…≥λp≥0；分别求出对应于特征值λi的特征向量ei

（i=1，2，…，p），要求‖ei‖=1，即 =1，其中，eij表示向

量ei的第j个分量，也就是说ei为单位向量。

2.3 计算主成分贡献率及累计贡献率

主成分贡献率为：

主成分累计贡献率为：

一般取累计贡献率达85%～95%的特征值λ1，λ2，…，λm所对应的第1、第2、…、第m（m≤p）个主成分。

2.4 计算主成分载荷

，主成分载荷就是zi与xj之间的相关系数（主成分不相关）。

2.5 各主成分的得分

各主成分的得分为：

3 图像处理及结论

众所周知，图像信息所含的数据量巨大。为了便于图像的存储，提高存储效率，研究图像压缩具有重要的意义。

主成分分析法在数字图像压缩中的的应用

鲁书山，沈小林，樊凯强

（中北大学，山西 太原 030051）

摘 要：阐述里主成分分析法的定义，及应用于实际的意义，通过matlab编程实现主成分分析法在图像压缩方面的应用，在编程过程中设置不同主成分个数来显示不同的处理结果。在对处理结果进行分析，同时也对主成分分析法的性质有了更直观的认识，方便日后在其他领域的应用。

关键词：主成分分析法；图像压缩；特征提取；matlab编程

中图分类号：TP309.7 文献标识码：A DOI：10.15913/j.cnki.kjycx.2016.23.098

主成分分析法是用降维的思想，用幾个互不相关的主成分反映原始变量的大部分信息的统计方法。能有效降低数据维度，减少计算量，在涉及到数理统计的各个领域均有广泛的应用。本文先介绍主成分分析的原理，再通过matlab用主成分分析法对图像进行压缩，实现主成分在图像处理中的应用。

1 主成分分析法概念及性质

1.1 概念

假定有n个样本，每个样本由p个变量构成，则可以组成一个n×p阶的数据矩阵：

. （1）

设x1，x2，…，xP为原变量，z1，z2，…，zm（m≤p）为新变量，则：

. （2）

系数lij为新变量对原变量的反应情况。

1.2 性质

zi与zk（i≠k；i，k=1，2，…，m；j=1，2，…，p）相互无关；z1是x1，x2，…，xP的一切线性组合中方差最大者，z2是与z1不相关的x1，x2，…，xP的所有线性组合中方差最大者；zm是与z1，z2，……，zm-1都不相关的x1，x2，…xP的所有线性组合中方差最大者。则新变量指标z1，z2，…，zm分别称为原变量指标x1，x2，…，xP的第1，第2，…，第m主成分。

通过以上表述可知，主成分分析的实质是计算主成分zi（i=1，2，…，m）所反映的原变量xj（j=1，2，…，p）上的荷载 lij（i=1，2，…，m；j=1，2，…，p）。它们分别是相关矩阵（也就是x1，x2，…，xP 的相关系数矩阵）m个较大的特征值所对应的特征向量。

2 计算步骤

2.1 计算相关系数矩阵

相关系数矩阵为：

. （3）

rij（i，j=1，2，…，p）为原变量xi与xj标准化后的相关系数，rij=rji，其计算公式为：

. （4）

2.2 计算特征值与特征向量

解特征方程|λI-R|=0，求出特征值，并使其按大小顺序排列λ1≥λ2≥…≥λp≥0；分别求出对应于特征值λi的特征向量ei

（i=1，2，…，p），要求‖ei‖=1，即 =1，其中，eij表示向

量ei的第j个分量，也就是说ei为单位向量。

2.3 计算主成分贡献率及累计贡献率

主成分贡献率为：

. （5）

主成分累计贡献率为：

. （6）

一般取累计贡献率达85%～95%的特征值λ1，λ2，…，λm所对应的第1、第2、…、第m（m≤p）个主成分。

2.4 计算主成分载荷

，主成分载荷就是zi与xj之间的相关系数（主成分不相关）。

2.5 各主成分的得分

各主成分的得分为：

. （7）

. （8）

3 图像处理及结论

众所周知，图像信息所含的数据量巨大。为了便于图像的存储，提高存储效率，研究图像压缩具有重要的意义。