基于二次变异多目标差分进化方法的水火电联合调度研究

张慧峰++解相朋++胡松林

摘要：针对水火电调度系统中同时存在的环境污染和火电站煤耗问题，本文提出了一种多目标自适应二次变异差分进化算法，运用自适应控制参数和Tent混沌序列改进了差分进化中的二次变异算子，结合基于密度熵的非劣前沿分布性控制策略，实时地控制了进化群体的收敛性和多样性，在提高了差分进化的收敛速度的同时有效地避免了“早熟”现象的发生。同时，考虑了水电系统中的网络损失问题，为了克服水火电系统中的非线性约束条件难以满足的问题，本文引入了启发式嵌套修正技术，对进化群体中的不可行个体进行循环修正，有效地解决了水火电系统中等式约束难题。此外，本文还将多目标自适应二次变异差分进化算法應用到水火电联合调度系统中，并取得了较为满意的结果。

关键词：水火电调度系统，环境污染，网络损失，二次变异，混沌序列，早熟现象

中图分类号： TV697 文献标识码：A 文章编号：1672-3791（2016）11（a）-0000-00

引言

由于环境污染越来越受到人们的重视，传统的以经济成本为主要目标的水火电优化调度已不能满足社会的需求，更多的学者也开始关注火电厂的污染排放问题[1-3]。为此，有的学者提出一种兼顾经济性和环保性的水火电联合优化调度模型，该问题也逐步变成许多学者关注的焦点问题。

传统的多目标优化主要通过将多目标问题转化为单目标问题的方法，再采用单目标进化算法进行求解。国外学者M. Basu在经过多个目标加权求和后，采用交互模糊满意度的方法求解了该问题，并取得了一定的研究成果[4]。K.K. Mandal通过差分进化算法对不同目标权重下的总目标进行优化运算，并分析比较了其结果的优劣程度[5]。

虽然上述方法可以一定程度上解决多目标优化问题，然而，由于在实际工程应用中，各目标的权重是难以精确描述的，因此，该转化策略的实用性不强。随后，国内学者马光文[6]将NSGA-II的多目标进化方法应用到水火电调度系统中，并产生了一系列非劣解集，为实际调度过程提供了足够的决策支持。在此，本文提出了一种多目标自适应二次变异差分进化算法（ASMMODE），运用自适应控制参数调节了群体的收敛速度，引入Logistic混沌序列增加了进化群体的多样性，从一定程度上避免了“早熟”现象的发生。同时，本文运用启发式嵌套修正的约束处理方法，有效地解决了水火电调度系统中的复杂约束问题，并将多目标自适应二次变异差分进化算法应用到水火电调度系统中，取得了较为满意的结果，从而为多目标水火电联合优化调度提供了一条新途径。

1 水火联合优化调度模型概述

多目标水火电联合优化调度主要是在满足水火电站出力约束、系统负荷平衡、水量平衡等约束条件的基础上，并同时对氮氧气化物排放量和火电经济成本进行优化[7-13]。

1.1 目标函数

（1）火电经济成本

（1）

其中， 为调度时间长度， 为火电站个数， 为第 个火电站第 个时段的出力， 为第 个火电站运行的成本系数， 为第 个火电站的最小出力限制。

（2）污染气体排放量

（2）

其中， 为污染排放系数。

1.2 约束条件

（1）系统负载平衡约束

（4）

其中， 为第 个水电站在时段 的出力， 为第 时段的电力传输损失。而水电站的出力则主要是由其库容和下泄流量决定。 为水电站数量， 为第 时段系统的负载需求。而水电站的出力由库容和下泄流量相关，其具体表达式如下：

（5）

而 为第 个水电站的出力系数， 和 为第 个水电站在 时段的库容和下泄流量。其中，电力传输损失一般可以表示为火电出力的函数，具体如下[13]：

（6）

其中， 为电力传输损失系数。

（2）水量平衡约束

（7）

其中， 为第 个水电站在 时段的来水， 为第 个水电站在 时段的弃水， 为第 个水电站上游与第 个电站有直接水力联系的电站数量， 为第 个水电站上游第 个电站的时滞时间长度。

（3）出力约束

（8）

其中， 为第 个水电站的最小和最大出力， 为第 个火电站的最小和最大出力。

（4）水库库容、流量约束

（9）

其中， 为第 个水电站的最小和最大库容， 为第 个水电站的最小和最大下泄流量。

（5）初末库容约束

（10）

其中， 分别为第 个水电站的初末库容。

2 多目标自适应二次变异差分进化

多目标自适应二次变异差分进化算法根据多目标进化算法特有的选择机制，将Pareto等级划分操作替代单目标差分进化的适应度函数比较过程[14]。并在差分进化算法的基础上加入了外部档案集的维护和修改操作，保留了进化群体中的精英个体[15]。结合混沌序列产生机制，对变异操作的参数进行改进，使得变异算子可以自适应地指导群体的进化过程。

2.1自适应二次变异的差分进化

由于传统的差分进化算法无法自适应地根据进化种群的多样性实时地改变进化策略，使得其优化效率较低或容易产生“早熟”现象。为此，本文提出一种自适应二次变异的差分进化方法。其一般形式如下：

（11）

其中， 为进化群体中三个不同的个体，且 为选自外部档案集的两个个体， 为个体进化参数， 为自适应调节参数，其表达式为：

（12）

其中， 为控制参数， 为当前进化代数， 为进化的最大代数。在一般情况下，差分进化的变异操作按照上述的形式进行。特别地，检查种群第 维多样性是否低于一定阈值即 ，多样性指标 表达式为：

（13）

其中， 为外部档案集大小， 为外部档案集个体的第 维变量， 为 的平均值， 为第 维变量最大和最小边界。

若 时，Logistic混沌映射被用来产生一组混沌序列 ，其序列产生方式为[16]：

（14）

其中， ，当 时，可以产生在 范围内的随机序列，且此时序列初始值满足 。而此时，结合混沌序列对进化中的种群进行二次变异，其表达式为：

（15）

由此，进化种群的多样性将会增大，搜索范围不仅仅局限于局部区域，当遇到多峰函数时，其优化结果不会陷入局部最优，从而避免“早熟”現象的发生。

2.2 基于密度熵的非劣前沿分布性控制

在多目标优化过程中，为了保留群体进化过程中的精英个体，制定了外部档案集的精英保留策略。该策略主要根据非劣前沿的分布特性制定精英个体的保留策略。在文献[15]中，非劣前沿的平均距离被用来作为其分布性指标，该方法在一定程度上保证非劣前沿整体的分布性，但是无法精确描述个体与个体之间的聚集程度。本文采用一种基于信息熵的非劣前沿分布性控制方法[17]，采用文献[14]中的相对距离控制非劣前沿上个体的聚集程度，从而提高其非劣前沿的分布性。

（16）

其中， 为个体 邻接的下方个体， 为个体 的相对距离， 则为个体 的熵值。由此，整个非劣前沿的密度熵可以表示为：

（17）

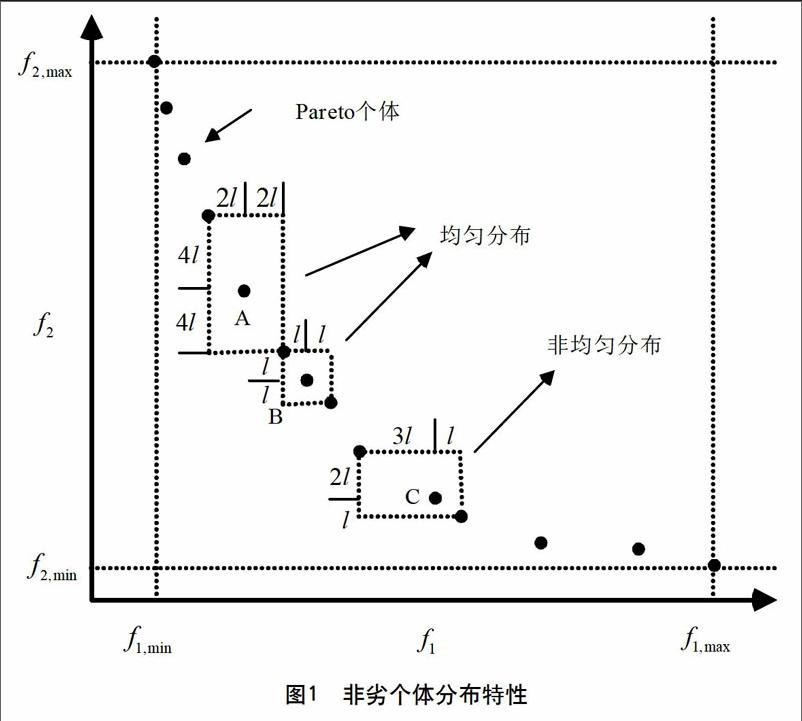
其中， 为外部档案集的大小。本文采用的密度熵法不仅考虑非劣前沿中个体的分布距离，还兼顾非劣前沿整体的分布距离。如图1所示，非劣前沿个体若出现A、B、C三种分布情况，则不难看出，C分布不属于均匀分布，若其中存在新加入个体，则应该剔除；而A和B分布均属于均匀分布，但B中个体距离相对整体的跨度而言，相对较小，仍然不符合整体的分布性要求。而A不仅具有均匀的个体分布距离，而且还符合非劣前沿整体的分布要求。因此，可以保留非劣前沿中密度熵较大的个体，从而提高非劣前沿整体的分布特性。

2.3 水火电系统约束处理方法

（1）编码

由于在整个水火电调度过程中，一般将下泄流量和火电出力作为决策变量对其联合优化模型进行求解。其具体表达式如下：

（18）

（2）约束处理方法

由于水火电联合调度过程呈现的高维、非线性和强耦合特性，各种复杂约束的处理效果对整体优化结果有较大的影响，所以高效的约束处理方法能提高优化的效率。约束处理的重点一般集中在水量平衡和系统负载平衡约束的处理上，由于水量平衡约束效果对负载平衡有后效影响，所以采取先处理水量平衡约束再处理负载平衡约束的方法。在此，本文采用文献[18]中启发式嵌套修正的方法，对水量平衡和负载平衡约束进行处理，并根据约束违反程度的标准界定个体的可行性，从而有效地将进化中的群体控制在可行区域内。

3 实例研究

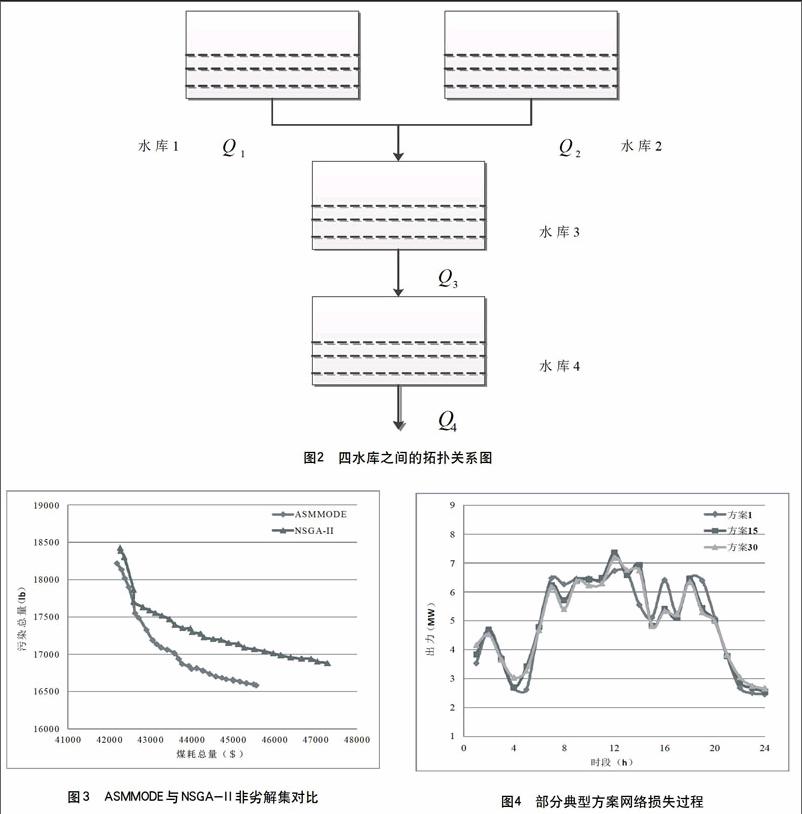
以四个水电站和三个水电站组成的水火电系统为例[4]，将本文提出的二次变异自适应多目标差分进化算法应用到该系统中，调度时段总长度为1天，每一个小时为一个时段，其四个水电站的拓扑结构如图2所示。该实例中关于水电站、火电站以及负载平衡等约束及相关数据均可参考文献[19-20]。

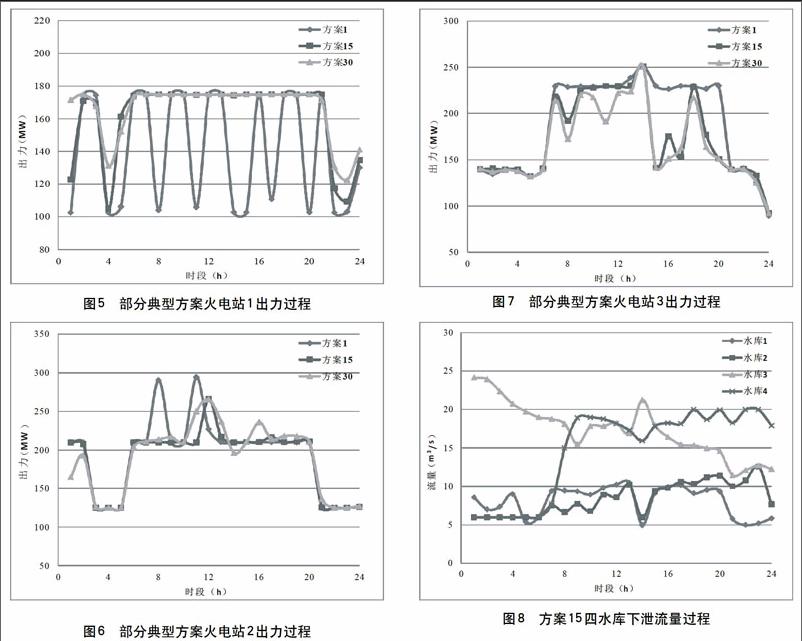
进化群体经过2000代的变异、交叉和选择操作后，在外部档案集中存储了30个非劣精英个体或非支配解，如图3所示。根据污染总量和成本总量的曲线图可知，污染气体排放总量和经济成本总量为相互矛盾和制约的关系。

通过和NSGA-II得到的结果对比，可以看到，多目标二次变异方法得到的解集处于NSGA-2解集的左下方，也就意味着该方法得到的最优方案集明显要优于NSGA-II，而在非劣方案集的分布特性特明显要好于NSGA-II。

MOCADE and NSGA-II）

而多目标二次变异方法求解得到所有非劣解集如表1所示，总煤耗量最小可以达到42193美元（方案1），总污染量最小可以控制在16581磅（方案30），而方案（15）的总煤耗量为43772美元，总污染量为16871磅。

为了进一步地分析非劣解集的优化方案，将方案集中的方案（1）、方案（15）以及方案（30）作为三种典型方案，并针对电力传输损失、各电站的出力过程进行深入剖析，如图4、5、6和7所示。方案（1）中的经济成本最小，方案（30）的污染气体排放量最小，方案（15）为折衷方案。图4中为三种典型方案下的网络传输损失对比结果，其大致趋势基本保持一致，网络传输损失基本保持在7.5MW以下，其不同主要集中在网络损失的波峰和波谷。图5、6和7为火电站1、火电站2和火电站3在三种典型方案下的出力过程。图5中三种方案下的出力过程基本保持一致，不难看出，相比其他两种方案，方案1的出力过程基本保持在最低状态，方案15次之，方案30最高。由于网络传输损失主要和各火电站的出力紧密相关，因此，火电站1可能对网络传输损失有较大影响。

同样地，在火电站2和火电站3中，三种方案下的出力过程也基本保持一致，但并不存在火电站1中类似的出力过程；而在火电站3中，不难看出，方案1的出力过程基本保持最高状态，方案15次之，方案30出力最低。

由于这三种典型方案代表着不同的利益背景，方案（1）经济成本最低，单从火电站生产运营的角度，该方案是最好的；方案（30）污染排放量最小，社会环境污染影响最低；而方案（15）相对折衷，在需要同时兼顾经济性和环保性的条件下，该方案为最佳方案。

（Figure.7 The output process of thermal unit 3 in some typical schemes）

本文以方案（15）为折衷方案，对其方案下的水电出力过程、库容变化和下泄流量过程进行深入分析。四个水电站的出力过程如图表2所示，不难发现，所有出力均被控制在出力约束允许的范围内，且在整个调度时段内装机最大的水库4始终维持最大的调节能力。

库容和下泄流量过程如图8和图9所示，其变化过程均控制在可行范围内。由于水库4具有最大的调节能力，且处于四个水电站的最下游，其库容和下泄流量在多数时间段内均维持较高状态。

（Figure.9 The storage process of four reservoirs in scheme （15））

综上所述，基于二次变异的差分进化算法能较好地同时优化污染排放量和经济成本，得出一系列非劣方案集。方案中各火电站出力、水电站出力及库容和下泄流量变化均满足各类约束条件，且将网络传输损失控制在较小范围内，最终得到的优化方案也进一步证明了该方法的可行性和有效性。

5 结论

本文考虑了节能环保多目标水火电优化过程中的网络损失问题，将线性等式约束问题推广到非线性等式约束问题，使得调度过程变得更加复杂。为此，本文根据多目标进化算法的特点改进了差分进化算子，提出了一种多目标自适应二次变异差分进化算法。并将该算法应用到该调度模型中，结果表明，多目标自适应二次变异差分进化算法经过一次运行后产生的非劣解集，不仅较好地解决了该复杂约束问题，而且同时具有较高的收敛精度和较好的分布特性。并根据非劣方案集选取符合实际需求的调度方案，制订了各火电站和各水电站的短期发电计划，为多目标水火电联合调度提供了一种新思路。

参考文献

[1]喻洁，季晓明，夏安邦，基于节能环保的水火电多目标调度策略[J]，电力系统保护与控制， 2009，37（1）： 24-27.

[2]吴杰康，唐力， 基于模糊机会约束规划的水火电力系统多目标随机调度模型[J]， 中国电机工程学报， 2011， 31（25）： 26-34.

[3]银车来，李光熹，熊曼丽，水火电联合系统多目标优化调度[J]，电力系统自动化， 1993， 17（9）： 30-34.

[4]M， B.， An interactive fuzzy satisfying method based on evolutionary programming technique for multi-objective short-term hydrothermal scheduling. Electr Power Syst Res， 2004， 69： 277-285.

[5]Mandal KK， C.N.， Short-term combined economic emission scheduling of hydrothermal power systems with cascaded reservoirs using differential evolution. Energy Conversion Management， 2009.50（1）： 97-104.

[6]张志刚， 马光文，基于NSGA-II算法的多目标水火电站群优化调度模型研究[J]，水力发电学报，2010，29（1）：213-218.

[7]袁晓辉，袁艳斌，张勇传，水火电力系统短期发电计划研究[J]，华中科技大学学报（自然科学版）， 2006， 34（4）： 70-72.

[8]杨锐，大系统分解协调法互联电网水库群长期随机优化调度计算[J]，电网技术，1990，4：1-7.

[9]李朝安，大型水火电力系统最优运行的分解协调原理[J]，电力系统自动化，1985， 5： 25-34.

[10]朱春涛，伍永刚，李彬艳，改进粒子群算法求解水火电系统短期负荷分配问題[J]，水电自动化与大坝监测， 2006， 30（6）： 12-15.

[11]张晓花， 赵晋泉， 陈星莺， 节能减排下含风电场多目标机组组合建模及优化. 电力系统保护与控制， 2011， 39（17）： 33-39.

[12]覃晖， 周建中， 基于多目标文化差分进化算法的水火电力系统优化调度. 电力系统保护与控制， 2011. 39（22）： 90-97.

[13]Lakshminarasimman L， Subramanian S. Short-term scheduling of hydrothermal power system with cascaded reservoirs by using modified differential evolution. IEE Proceeding Generation， Transmission and Distribution， 2006； 153（6）： 693-700.

[14]Storn， R. and K. Price， Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces. International Computer Science Institute-Publications-TR， 1995.

[15] Deb K， Pratap A. A fast and elitist multi-objective genetic algorithm： NSGA-II. IEEE Trans Evol Comput 2002； 6（2）：182-97.

[16] E. Ott， Chaos in Dynamical Systems， Cambridge University Press， Cambridge， UK， 2002.

[17] Huifeng Zhang， Dong Yue， etc. Multi-elite guide hybrid differential evolution with simulated annealing technique for dynamic economic emission dispatch， Applied Soft Computing， 2015， 34： 312-323.

[18]Lu Youlin， Zhou Jianzhong， Qin Hui， et al.， A hybrid multi-objective cultural algorithm for short-term environmental/economic hydrothermal scheduling， Energy Conversion and Management， 2011； 52（5）： 2121-2134.

[19]Basu M. A simulated annealing-based goal-attainment method for economic emission load dispatch of fixed head hydrothermal power systems. Electr Power Energy Syst 2005；27（2）：147-53.

[20] Hota， P.K.， A.K. Barisal and R. Chakrabarti， An improved PSO technique for short-term optimal hydrothermal scheduling. Electric Power Systems Research， 2009. 79（7）： 1047-1053.

通信作者：张慧峰（1985-），男，讲师；研究方向为能源优化调度。