如何利用图像特征以巧解高中数学函数题

李沐霏

【摘要】函数知识是高中数学知识的重要组成部分，函数图像的合理性解析，可以提高函数题目的解题准确性，结合高中数学中相应的函数图像特征，对利用函数图像巧解高中数学函数进行分析。

【关键词】图像特征 高中数学函数题 巧解分析

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2016）33-0183-01

高中函数的知识涉及面较广，在高中数学知识的应用中具有中的作用，函数中一部分是数学关系式，另一部分是函数图像，我们在日常数学函数学习中，可以充分利用函数图像的特征进行解题，可以提高高中函数的解题效率和准确性，促进高中生的函数的灵活应用。

一、高中函数图像的基本特征归纳

高中函数知识在高中数学知识结构中占据较大的比重，也是高考数学考试中主要的考核点之一，合理应用函数图像进行解题，提高高中数学的习题做题效率，保障解题准确性，结合高中数学函数的相关知识，对高中函数图像的特征进行归纳。其一，高中函数图像中体现函数因变量和自变量的关系[1]，例如：我们依据一次函数图像，总结直线表示自变量和因变量的关系，而二次函数中应用对称的曲线表示因变量和自变量之间的关系；其二，高中函数图像一般具有一定的规律性。例如：三角函数的图像中自变量和因变量之间呈现有规律的波动图像，而二次函数图像则是应用对称的抛物线表示函数关系；其三，高中函数中一些函数图像中存在最值问题[2]，例如：我们解决二次函数中具有最大值和最小值的问题，为一次函数图像在毫无题目条件的前提下，不具有最值问题。实现高中函数图像在函数题目中的综合应用，是实现函数知识灵活应用的基础。

二、高中函数图像的基本特征在解题中的巧用分析

（一）通过函数图像确定丰富解题知识点

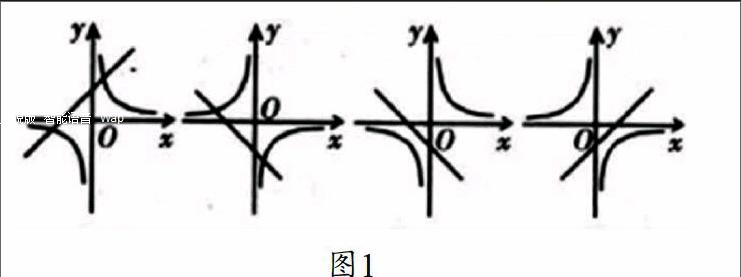
高中函数图像的基本特征，是巧解高中题目的主要途径之一，有时，我们可以从函数图像的基本特征，判定函数题目的解题思路，丰富函数习题的解题知识点。例如：某函数题目为“函数y=k/x（k不为0）以及函数y=k（1-x）这两个函数图像在统一坐标系中表示出来的图像是哪个？如图1[3]。”这类判断函数图像的问题，在高中数学函数的考察中经常出现，依据函数的基本特征，我们通过以上两个函数关系式进行判斷，假设K的取值为正数，y=k/x的图像必经过一、三象限，而y=k（1-x）的图像经过二、四象限；假设K的取值为负数，那么，我们可以判断y=k/x的图像必经过二、四象限，而y=k（1-x）的图像经过一、三象限。结合以上对函数图像的初步确定，可以初步形成对题干中函数图像的判定，从而利用函数图像的基本图像特征，得出函数题目的答案，经过对题目中函数图像特征的总结，最终确定题目的答案为左边数第三个图像为最佳答案。我们在学习函数知识中，合理把握函数图像的基本特征，可以为解答函数数学题提供丰富的知识参考，补充高中函数题目中的基本知识结构，从而达到提高数学结题效率中的作用。

（二）通过函数图像确定题目的答案

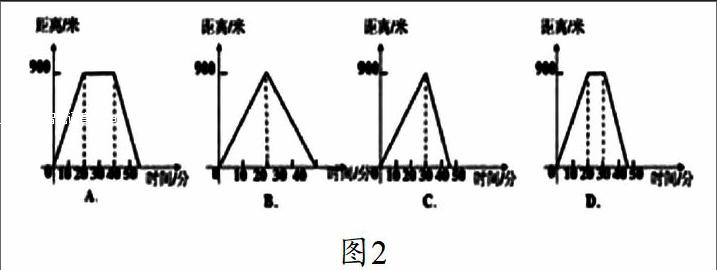
函数图像的解题中应用函数的基本特征，可以在高中数学的解题中轻松的确定题目的答案，这种函数图像解题方式，在高中函数题目的解题中，选择题的结题应用效果相对明显，例如：高中函数题目为：“A每天的身体锻炼时间与路程图，从家出发后，用了20分钟的时间达到了离家900米的地方，由于身体原因A在原地休息了10分钟之后，接着用了15分钟的时间跑回了家中。如果我们可以用y来表示距离，用x来表示所用的时间，那么下列的函数的函数图像中表示正确的是哪个？如图2[4]”这种函数图像混应用的函数选择题，在函数图像基本特征的知识点中考核题型较常见，从题干的描述中，可以得知：题干的图像主要分为三部分，路程为别为：900米，0米，以及15X米，从函数图像的初步判定来看，函数图像中符合下题干分段函数的基本要求的选项为A、D两项，经过进一步对题干中已知条件的判定，可知中间的休息时间为10分钟，从而更近一步判定函数图像的进一步确定，A之间的间隔时间为20分钟，D的时间间隔时间10分钟，由此可以判定，函数题目的最终选择题答案为D选项，实现函数图像基本特征在题干中的合理应用，可以提高高中函数题目的结题速率，同时也可以实现对函数题目的结题思路更加明确化发展，为实现高中函数知识的灵活应用提供完善的知识应用体现。

（三）应用函数图像判定题目的准确性

高中函数图像基本特征在解决高中数学问题上，得到充分的应用，应用函数图像的基本特征，可以对函数图像进行解题准确性的判定。例如：高中函数图像的题目为“函数y=k/x（k不为0）[5]，当K值为负整数时，函数图像的变换空间为的最大值为多少？”求函数的最大值或者最小值问题，也是高考函数知识考察中经常出现的一类函数问题，从题干中我们可以推断函数图像，当K为负数时，函数图像必经过二、四象限，那么，题干的函数图像中就只有最大值的问题，函数图像呈现弯曲的曲线状态，图像的最值分别存在域二四象限之中，因此函数值越接近原点，函数图像的最值越大，因此，当K的取值越小，图像的函数值的值越大下大，因此，此时题干的最终答案为-1。

三、结论

函数知识的应用，在高中数学的学习各个领域都有所涉及，结合高中函数图像的基本特征，对函数图像在高中数学题的解题中的巧用进行分析，总结干活中函数学习中图像应用的基本规律，明确函数题目的解题思路，提高函数知识的利用效率。

参考文献：

[1]白雪.高一与初中数学教学衔接存在问题与对策研究[D].天津师范大学，2014.

[2]傅婷.基于翻转课堂教学模式的高中函数教学实践研究[D].陕西师范大学，2014.

[3]陈鑫笑.高中函数学习障碍分析及教学对策研究[D].洛阳师范学院，2016.

[4]白潇.高中生解决函数问题审题环节的案例分析[D].天津师范大学，2012.

[5]王红玮.初高中数学中函数模块教学衔接问题的探讨[D].延边大学，2015.