AHP法在高师院校数学实验室人才培养模式中的应用

方秀男++汤凤香++李东++张菊红++方海文

摘 要：文章分析了对高师院校数学实验室人才培养的影响因素，建立了相应的评价指标体系，同时给出了反映各个指标重要性的判断矩阵，提出了从实验室建设、实验教学和大学生科技创新这三方面的实验室人才培养模式，通过AHP法，将定性问题转化为定量问题进行分析，较好了刻画了各个指标的重要性程度，以期对决策者进行有关决策提供依据。

关键词：人才培养模式 AHP法 评价指标体系

中图分类号：G65 文献标识码：A 文章编号：1674-098X（2016）11（a）-0118-02

近年来，实验教学已成为高校教育工作中的重要环节，实验室作为最基本的教学设施，不但要完成学生的实验教学，而且承担着科学研究、技术开发、创新交流以及社会服务的重要任务，更是培养大学生实践能力的主阵地，如何合理地建立实验室人才培养机制是首要的问题。该文利用层次分析法，即AHP法尝试对人才培养所做的决策进行科学评价。

1 数学实验室的人才培养模式

1.1 从实验室建设的角度探索人才培养模式

知识经济时代，数学实验室如何摆脱传统教学模式的束缚，激发学生的思维积极性与创造性， 培养学生严谨求实的科学精神和培养学生数学实践能力。为此，实验室建设应该围绕人才培养目标而展开，只有建立健全的实验室建设规划和实验室管理制度，并以此为基础，才能更好地为专业人才培养提供服务。有关实验室建设的目标容易制定，关键是要对目标实施的效果进行评价和总结。例如，实验室的布局是否合理，实验室的软硬件配置是否满足教学需求，实验室的规划是否适应教师和学生的实际情况等等。

1.2 从实验教学的角度探索人才培养模式

从师资队伍的建设、教材建设、教学内容的改革、学生反馈信息的分析等角度探索数学实验在专业课程中的人才培养模式，其中的关键问题是隐含的信息，例如教学内容的改革不是凭空提出的，这是需要实践教学检验的，除了可以从考核当中找到相关信息，学生方面的反馈也是需要实际调研的。

分析数学实验室如何根据现有条件安排学生的职业技能训练内容。关键问题是能合理地将学生的职业技能训练加入到实验内容当中。师范生需具备深厚的教师职业技能，如多媒体课件的制作，几何画板的使用，应用数学软件解决实际问题，查阅文献资料等，因此数学实验室还可以提供可控制的教学环境，通过音视频记录装置和实验室式的教学练习，对需要掌握的知识技能进行选择性的教学模拟，使师范生的各种教学行为的训练变得可被观察、分析和评价。将开展数学实验与锻炼教师职业技能紧密联系在一起，努力提高其综合素质，这也是符合高师院校人才培养的目标的。

1.3 从大学生参与科技创新实践活动的角度探索人才培养模式

目前，以数学实验室为依托的各类竞赛活动越来越受到高校的重视，比如全国大学生数学建模竞赛活动，因而，从数学实验室参加诸如全国大学生数学建模竞赛的经验、得失探索人才培养模式就显得很有意义了。关键问题是，从目前情况来看，高师院校数学建模竞赛等活动的参与范围比较小，主要局限于数学本专业的学生，因此还需考虑如何在现有条件的基础上使更多其他学院的学生参与到竞赛当中来。

此外，近年来，越来越多的大学生参与教师教科研课题研究中来，但由于教师每年主持的课题有限，因此如何能够使更多的对相关问题有兴趣的同学参与进来，对于学生综合素质的提高是相当有意义的。从近年来高师院校鼓励学生进行科技创新活动、历年的规模和质量出发，对人才培养模式进行探讨是近期有关研究的热点，但难点是由于有关活动开展的时间不长，其与人才培养的关联性可能并不是很显著。

2 数学实验室的人才培养的评价指标体系

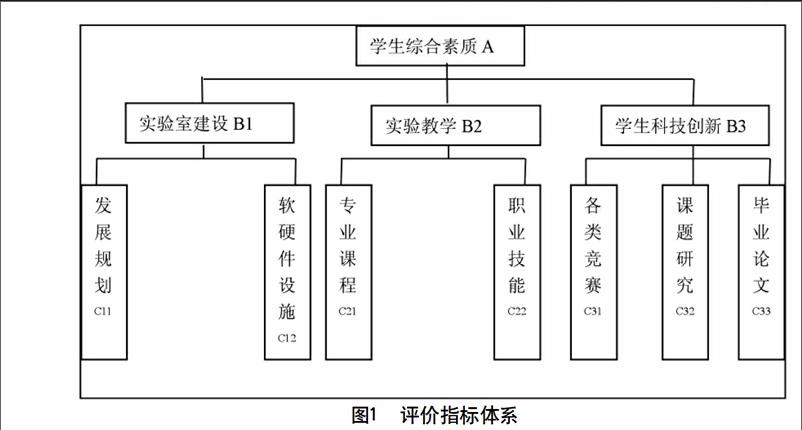
结合有关文献，并从以上的分析出发，建立了如下AHP评价指标体系，见图1。

整个指标体系是一个三层的层次结构，其中底层节点是影响人才培养模式的各个具体指标，称为“方案层”（用C来开头表示）；第二层为“准则层”（用B来开头表示），它将若干相关的指标组织为一个类，以反映人才培养在某个更大的范畴中的表现；顶层为“目标层”（用A来表示），它只有一个节点，表示最终人才模式的评价结果。通过调查问卷以及专家打分的形式，给出了各个指标层之间、指标层各个指标之间的相对评价标准，并构建了相应的判断矩阵，分别用A，B1、B2、B3表示。

利用层次分析法中的和法求得矩阵A的归一化特征向量[0.142 9，0.5714，0.285 7]，对应的近似最大特征值为

，并根据一致性指标得到：

，且，通过了一致性检验。类似地可以得到方案层的各个矩阵的有关数据表。由结果可知，均通过了一致性检验。前面计算的“方案层”指标的权重都是指指标在其所属的“指标类层”中的权重，为了通过细化的“子指标”来计算最终评价结果，需要将“方案层”在“准则层”中的权重转换为在“目标层”中的绝对权重。只要将判断矩阵B1、B2、B3所对应的向量w的各个分量值乘上“目标层”判断矩阵中对应的分量值即可。即，

B1：=（0.333 3，0.666 7）×0.142 9=（0.047 6，0.095 3）；

B2：=（0.833 3，0.166 7）×0.571 4=（0.476 1，0.095 3）；

B3：=（0.333 9，0.089 2，0.567 9）×0.285 7=（0.095 4，0.025 5，0.162 2）。

因此，方案层七个指标在人才培养模式所占的重要程度为：（0.047 6，0.095 3，0.476 1，0.095 3，0.095 4，0.025 5，0.162 2），数值的大小反映了各个指标的重要程度。此外，人才培养模式的综合评价值可以通过以下公式进行计算：，其中为第个子指标的评价值，为第个子指标在综合评价中的绝对权重。值一般取1、2、3、4、5中的一个，依次可表示为“很差”“较差”“合格”“较好”和“很好”。应用上述方法，根据调研情况可以得到相应的结果。

3 结语

该课题的研究从高等师范院校人才培养的目标出发，结合作者所在数学实验室的发展现状，同时考虑到数学相关专业师范类的特点，将AHP法与决策论的思想相结合，利用层次分析法的思想方法，尝试探索数学实验室培养高素质人才基本模式，具有比较重要的现实意义。

这项研究给出了高师院校数学实验室人才培养的评价指标体系，同时给出了反映各个指标重要性的判断矩阵。判断矩阵的元素可以通过调查问卷的方式进行统计得到，也可以通过专家评价的方式统计后得到。通过AHP法，将定性问题转化为定量问题进行分析，较好地刻画了各个指标的重要性程度，这将对决策者进行有关决策提供依据。此外，通过对各个指标层的单层排序，并且利用各个指标层之间的关系进行综合排序，能够给出当前决策的最终评价结果，这也对各项决策的最终效果提供较好的依据，同时目前的研究成果对于该课题的可持续性研究奠定了基础。

参考文献

[1] 钱伟，胡玉娟.高校理化实验室火灾风险的AHP法评估[J].实验室科学，2011（2）：185-189.

[2] 龙海波.应用AHP法建立本科院校重点实验室建设的评价指标体系[J].金融理论与教学，2013（2）：90-94.

[3] 王伟，隋小龙，郑建毅.AHP方法在公共建筑冷熱源方案选择中的应用[J].建筑技术开发，2015（10）：57-60.