A GA approach to vehicle routing problem with time windows considering loading constraints①

Liu Jiansheng (刘建胜), Luo Zhiwen, Duan Duanzhi, Lai Zhihui, Huang Jiali

(*School of Mechanical and Electronic Engineering, Nanchang University, Nanchang 330031, P.R.China) (**School of Management, Shandong University, Jinan 250100, P.R.China)

A GA approach to vehicle routing problem with time windows considering loading constraints①

Liu Jiansheng (刘建胜)*, Luo Zhiwen*, Duan Duanzhi②*, Lai Zhihui*, Huang Jiali**

(*School of Mechanical and Electronic Engineering, Nanchang University, Nanchang 330031, P.R.China) (**School of Management, Shandong University, Jinan 250100, P.R.China)

As a new variant of vehicle routing problem (VRP), a finished vehicle routing problem with time windows in finished vehicle logistics (FVRPTW) is modeled and solved. An optimization model for FVRPTW is presented with the objective of scheduling multiple transport routes considering loading constraints along with time penalty function to minimize the total cost. Then a genetic algorithm (GA) is developed. The specific encoding and genetic operators for FVRPTW are devised. Especially, in order to accelerate its convergence, an improved termination condition is given. Finally, a case study is used to evaluate the effectiveness of the proposed algorithm and a series of experiments are conducted over a set of finished vehicle routing problems. The results demonstrate that the proposed approach has superior performance and satisfies users in practice. Contributions of the study are the modeling and solving of a complex FVRPTW in logistics industry.

finished vehicle logistics (FVL), vehicle routing problem (VRP), genetic algorithm (GA), time windows

0 Introduction

The automobile industry plays an important role in the world economy. According to statistical data from the Chinese Association of Automobile Manufacturers (http://www.caam.org.cn), 24.5 million vehicles were produced and 24.6 million vehicles were sold in China in 2015. Every year finished vehicles are transported from manufacturers to dealers in China. Finished vehicle logistics (FVL) has become a key component of the automobile industry, which can be characterized as follows: the dealers’ orders of finished vehicles are from manufacturers, and then some finished vehicle logistics companies are assigned to transport these finished vehicles. Vehicle loading and routing schedules consider packing feasibility and routing cost. As a variant of the vehicle routing problem (VRP), the finished vehicle routing problem (FVRP) is a practical routing problem with some constraints. Different from the traditional VRP, both the finished vehicles and transport vehicles are irregular three-dimensional shapes considered as geometry constraints. Especially, dealers pay more attention to knowing if the ordered vehicles would be arrived in time, which leads to that time window constraint with penalty function becomes an important factor in FVRP. To the best of our knowledge there are considerable researches reported on VRP. However there is a little published research on FVRP. In practice, FVRP is done by a scheduler’s experience or through simple heuristics. However, some factors involved make it difficult to be achieved by personal experience or simple heuristics. Meanwhile, increasing industry competition makes the problem more challenging. This research contributes to this complex problem by a practical solution in FVL.

1 Problem overview

The basic FVRP consists of known customers that require a number of finished vehicles to be delivered. Transport vehicles dispatched from a main depot must deliver all the ordered finished vehicles, and then return to the original depot. Each transport vehicle can carry a limited weight, and be only allowed to visit each customer one time. The objective is to find a set of vehicle routes satisfying these demands with minimal total cost. In practice, this is often taken to be equivalent to minimizing both the number of transport vehicles and their total distance.

Here the optimized solution is to select ordered finished vehicles to load and the transport vehicles into which to load them, and determine a set of routes satisfying all customers within given time. Otherwise, there will be a penalty, such as delay fee. The problem is called finished vehicle routing problems with time windows constraint (FVRPTW).

(1)

s.t.

where m: The number of transport vehicles

Cj: Transport cost of transport vehicle j

Tj: Time cost of transport vehicle j

(1) Weight limitation: It is assumed that any type of finished vehicles can be loaded in any type of transport vehicles. For the same reason, any type of transport vehicles can transport any kind of finished vehicles. However, the loading weight capacity of each fleet vehicle is limited. The total loaded weight of all finished vehicles must not exceed an upper limit of the loading weight capacity of the selected transport vehicles.

(2) Volume limitation: The same with the weight constraint above, the total volume of all the loaded finished vehicles cannot exceed the total allowed volume of the transport vehicles. Different from the traditional VRP, both the shape of the finished vehicles and the loading space of the transport vehicle are irregular, the volume constraint is specified as a 3D constraint, including length constraint, width constraint and height constraint.

(3) Order splitting rule: Small scale orders must not be split and only be serviced by one transport vehicle in order to minimize the routing cost. However, large scale orders can be split among multiple transport vehicles if their transport tasks exceed the limit of any transport vehicle. After fully loaded by several transport vehicles, the remained small tasks of the large scale orders are still required to be delivered by only one vehicle.

(4) Time windows: It is assumed that each transport vehicle moves at a constant speed, and each customer has a requirement to delivery time. If the transport vehicle arrives early, it must wait or may incur an early fee. Conversely, if the transport vehicle arrives late, it will incur a delay fee.

(5) Loading sequence: When a customer is visited, it should be possibly easy to unload. The finished vehicles of customers earlier on the route should be placed close to the rear of the transport vehicle. This is similar to LIFO.

2 Literature review

2.1 VRP problem

As a variant of VRP, when the loaded finished vehicle is the same style, that is the length is equal or almost equal, it can be determined by bin packing approaches (Hopper & Turton[1]; Lesh, et al.[2]; Fuellerer, et al.[3]; Leung, et al.[4]; Hu, et al.[5]). When the sizes of the finished vehicles vary widely but the loading spaces of transport vehicles are regular, 3D bin packing algorithms can be applied (Pisinger & Sigurd[6]; Tarantilis, et al.[7]; Bortfeldt[8]).When both the shape of finished vehicles and the spaces of transport vehicles are regular, many useful research results are available (Iori, et al.[9]; Gendreau, et al.[10]; Moura and Oliveira[11]; Zachariadis, et al.[12]; Lai, et al.[13]; Vidal, et al.[14]).

Different from traditional VRP, both the shape of the finished vehicles and loading space of the transport vehicles are irregular, which leads to more complex constraints in FVRPTW.

2.2 FVRP problem

As a pioneering study on operations optimization and management of FVL, Holweg and Miemczyk[15]assessed whether an FVL system could support a “build-to order” business. Mattfeld & Kopfer[16]developed an automated planning and scheduling system to support operations to transport finished vehicles from a transshipment hub by integrating the manpower planning and inventory control using a hierarchical approach. Wu[17]analyzed the development trend of FVL in China and a strategy of resource integration was put forward. Jing[18]analyzed why the finished vehicle logistics costs in China were high and discussed how to lower the costs. Kim, et al.[19]presented an approach for RFID-enabled finished vehicle deployment planning at a shipping yard. Hu[5]addressed the finished vehicle transporter routing problem and designed an evolutionary algorithm to solve medium and large scale problems. However the time window constraint was not considered.

In conclusion, there are not existing methodologies that can be directly used to solve the problem without substantial modification. To the best of our knowledge, this is exploratory research work to consider both time windows and penalty factors in FVRP. Furthermore, FVRPTW is NP-hard since it can be reduced to the general VRP which is a well-known NP-hard problem (Tasan & Gen[20]), and a small FVRPTW could create significant complexity, calling for substantial amount of time to solve. Therefore, an enhanced genetic algorithm is developed to solve the problem.

3 Solution modeling

In the model, all known customers are supplied from a main depot. Only one transport vehicle is allowed to supply each customer in the time windows [et, lt]. Moreover, any transport vehicle is subject to a loading weight limit Gi, loading length Li, and height Hi. The optimization is to determine a set of routes satisfying all customer orders at minimal cost by a fleet of transport vehicles for a given time interval. Here assumptions are as follows:

(1) Every customer can be serviced only one time by one transport vehicle, and then the transport vehicle will return to the original depot.

(2) A linear relationship exists between vehicle travel cost and distance.

(3) Each customer’s order must be delivered by only one vehicle.

(4) In order to minimize the inconvenience of goods receipts and customers’ service cost, no customer’s order can be split.

(5) There are enough available transport vehicles. The number of transport vehicles is expected to be minimized since the upfront cost of a transport vehicle is assumed to be very large.

(6) All customers should be served within given time, otherwise, an early/delay fee is imposed.

Let customer cibe supplied with different types of finished vehicles with quantity, weight, length, width and so on. The optimization model of the FVRPTW is proposed as follows:

F=min(F1+F2+F3)

(2)

(3)

(4)

(5)

s.t.

(6)

(7)

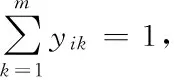
(8)

(9)

(10)

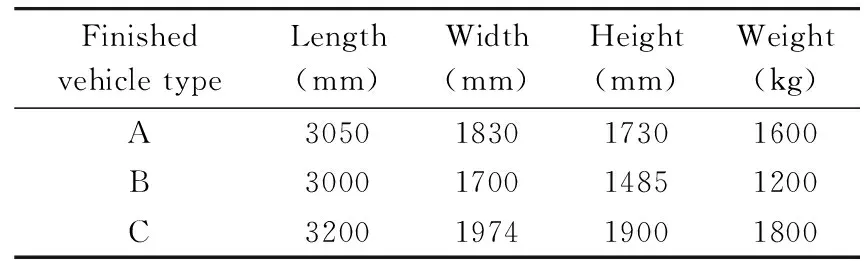
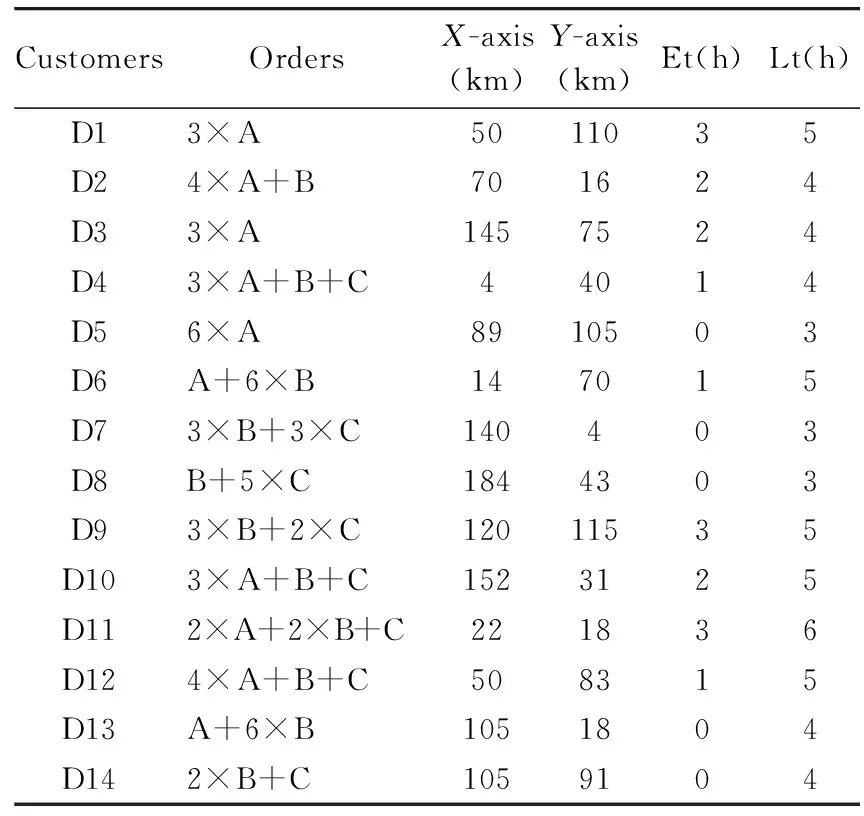
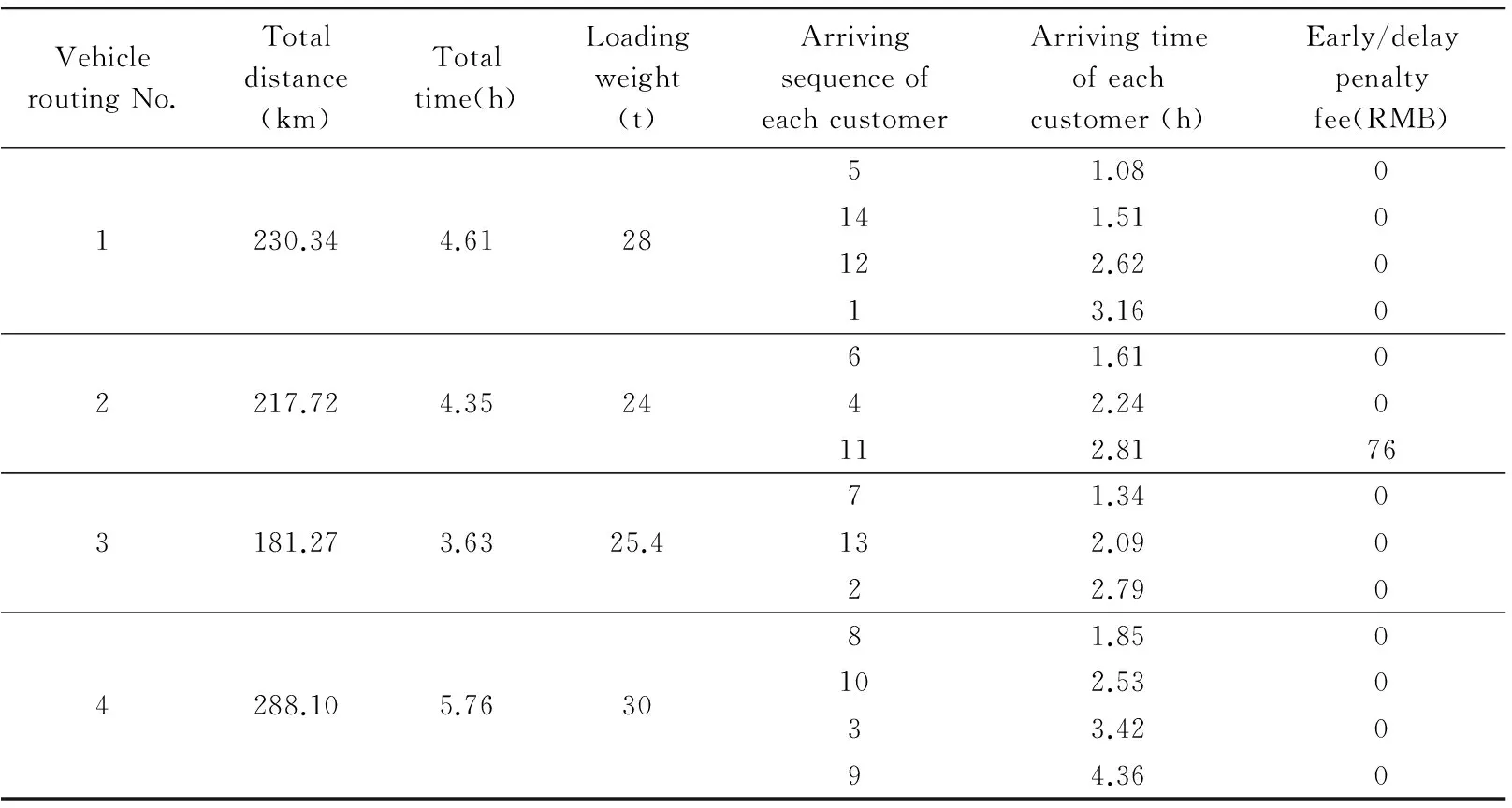
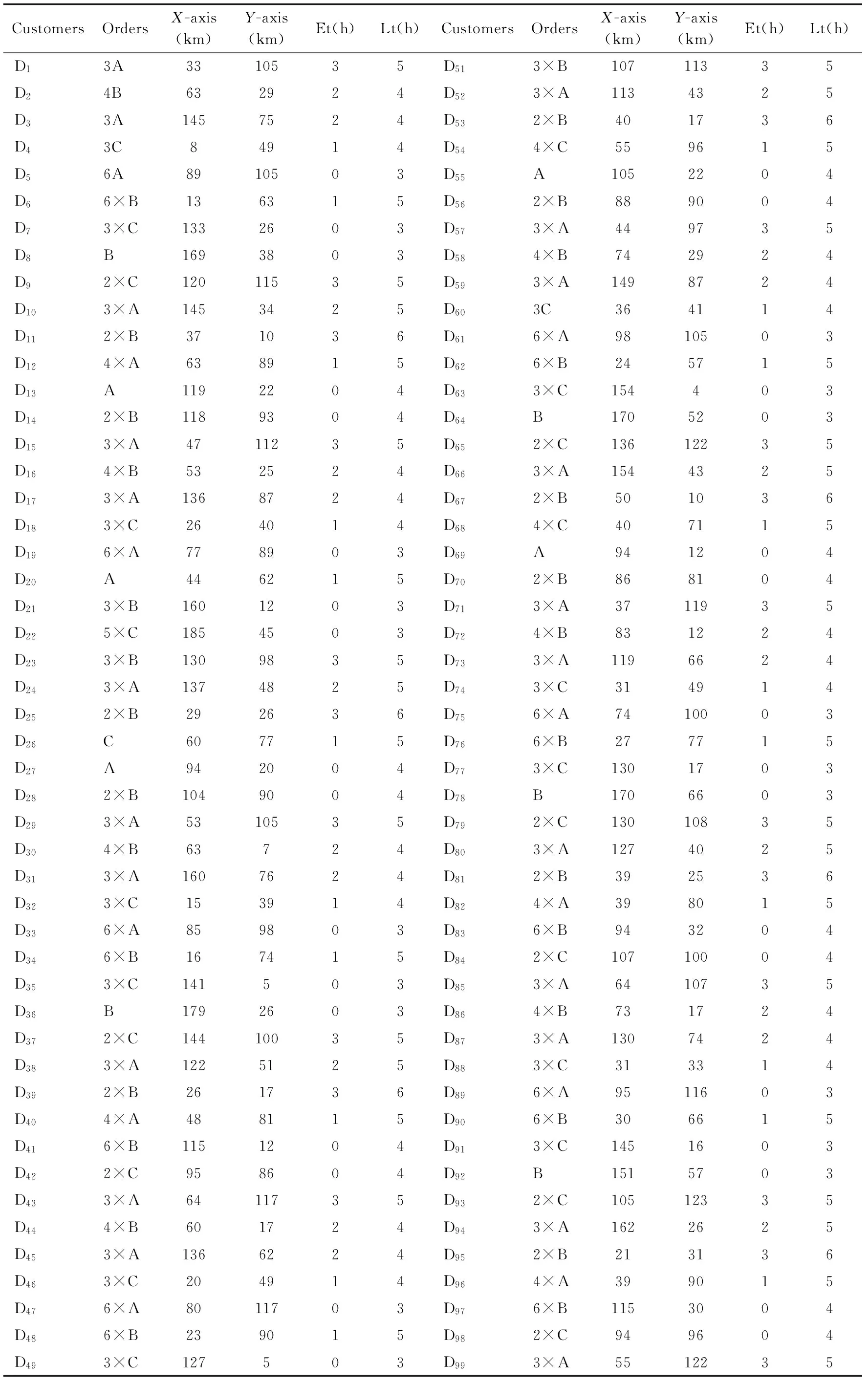
eti

(11)

(12)

(13)

(14)

(15)

Notation:

M: The number of transport vehicles

cij: The cost from customer i to customer j

Pe(t): Early penalty factor

Pl(t): Late penalty factor

tj: The actual time of the transport vehicle arriving to node j

[etj, ltj]: The time windows of the transport vehicle arriving to node j

gi: The total weight of finished vehicle at the node i

Gk: Standard loading weight of vehicle k

li: The total length of finished vehicle at the node i

Lk: Standard loading length of vehicle k

Objective Eq.(2) minimizes the total cost. Constraint (6) is the weight limitation of the transport vehicle. Constraint (7) is the length limitation of the transport vehicle. Constraint (8) ensures that only one transport vehicle is allowed to supply each customer. Constraint (9) limits that only one transport vehicle is allowed to visit one customer. Constraint (10) limits that only one transport vehicle is allowed to leave one customer. Constraint (11) enforces every customer’s order must be serviced in given time. Constraint (12) and Constraint (13) ensure the transport vehicle starts and returns to the main depot. Constraint (14) and Constraint (15) limit the value range.

4 Proposed algorithm

Genetic algorithms (GA) have been used for VRP incorporating time windows (Baker & Ayechew[21]). In this work, a GA algorithm is devised for this complex problem.

1) Encoding

Encoding is to convert the vehicle routes into the chromosome. In detail, the string of the customers in N=(1, 2,…, n) is used as chromosome for encoding, in which each gene represents a customer and their sequence represents the vehicle routing. Because there exist some constraints of the transport vehicle, such as total loading weight limit, 3D size limit, time windows and so on, and the transport vehicles must return back to the main depot, it is needed to insert ‘0’ into the customer’s sequence when the fitness value is evaluated and ‘0’ represents the main depot. For example, the sequence (0,1,2,3,0) means that the transport vehicle starts from the main depot and visits customer 1, customer 2, and customer 3 sequentially and then returns back to the main depot. So each ‘0’ in the string shows there are multiple transport vehicles and routes. For example, the chromosome “012308760” represents two routing. The first routing is 0-1-2-3-0, and the second routing is 0-8-7-6-0.

2) Initialization

Initial population is the origin of genetic algorithm, and its composition structure has a great impact on the consequence of its evolution. All finished vehicles in each customer’s order are assigned to the first transport vehicle according to chromosome sequence. When the maximum loading weight is greater than the sum weight of a1, a2,……, ai, and less than the sum weight of a1, a2, …, ai, ai+1, the substring “a1, a2, …, ai” is attained to represent the customers served by the first transport vehicle. The customers (a1, a2,…, ai) served by the first vehicle will no longer be considered. Start with the Noi+1customer. Repeating as above, the No.2 substring (ai+1, ai+2, …, ai+m) can also be attained for the second vehicle. Finally, all finished vehicles are loaded into the transport vehicles. By the way the initial chromosome can be gained continually until the number of chromosome equals to the scale s of initial population.

3) Fitness function

The objective is to minimize the total cost over multiple routes. So the total cost is directly taken as the fitness function. Because there are additional constraints, including time windows, loading weight and penalty factors, the fitness function is adjusted.

For the time windows constraint, if it is a hard time window problem, when arrival time is not in the given time window, the value of fitness function is set as ∞ (death penalty). If it is a soft time windows problem, the delay is allowed and penalized.

4) Selection operator

The top twenty percent of the population is double duplicated to the next generation. The middle sixty percent of the population is copied to the next generation. And the last twenty percent is abandoned.

5) Crossover operator

Offspring is produced from the parent solutions using a standard crossover procedure with point crossover, in which one point in the chromosome is chosen randomly. One offspring consists of the gene values from the second parent gene which are to the right of the point along with the gene values from the first parent gene. And then the duplicated existing members of the population are discarded. The crossover method is as follows:

A=1 2 3 4 5 6 7|8 9 10 11 12 13 14 15

B=15 14 13 12 11 10 9|8 7 6 5 4 3 2 1

First, move all the number after the crossover number ‘8’ in B to the front of A, and then A is:

A=8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Second, because one customer can only be served by one transport vehicle, the gene number must not be repeated in chromosome coding. Then the repetition number in A should be discarded, that is ‘1 2 3 4 5 6 7 8’，and then A is:

A=8 7 6 5 4 3 2 1 9 10 11 12 13 14 15

The same with A, B is:

B=8 9 10 11 12 13 14 15 7 6 5 4 3 2 1

6) Mutation operator

Mutation operator is realized by swapping position randomly. For example, 10 and 4 are swapped:

A=1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Then it will turn to be as follows after random exchanging position.

A=1 2 3 10 5 6 7 8 9 4 11 12 13 14 15

7) Improved termination condition

In general, the termination condition is the maximum iteration time. Here a new termination is provided, that is the algorithm will be terminated after the same optimization result is repeated twenty times. To prevent the next generation being worse than parent generation, the optimal individual strategy can be adopted, which is to keep the parent generation with the best value of fitness function to the next generation. By the way the search process is on the way to the optimal solution. Moreover, two convergence rules are adopted, total evolutionary times and the optimization results are the same for many times. When each convergence rule is satisfied, it will be thought convergence. It will save much calculation time by two convergence rules.

5 Computational experience

The presented algorithm is coded in Matlab R2010b and tested on a PC with an Intel 3.7 GHz processor, 4.00 GB RAM, and the Microsoft Windows 7 operating system. To our knowledge, there are no instances publicly available, and therefore a real situation in China is given to illustrate the approach.

The finished vehicles and available transport vehicle are listed in Tables 1 and 2. Here, let the loading weight of the transport vehicles be 30t, and the transport cost be 5RMB/km, and the transport velocity (v) be 50km/h. Let the main depot be located at the coordinate point (92, 51). Fourteen orders from the depot to dealers are listed in Table 3. Each order includes ordered finished vehicles, the customer’s coordinates, and time windows.

Table 1 Finished vehicle information

Table 2 Transport vehicle information

Table 3 Customer orders information

If an early or delay arrival is allowed (soft time windows) and Constraint (11) is inactive, an additional penalty fee will be created, which will be calculated into the total cost. In this case, penalty factors (Pe(t), Pl(t)) both are 400 RMB/h. Here initial population size is 100, the iteration time is 300, crossover rate is 0.7 and the mutation rate is 0.1. Then the total minimum routing cost is 4665 RMB and total run time is about 2s. There are four routing schedules, which are shown in Table 4.

If all transport vehicles must arrive in time (hard time windows), no delay is allowed. Then there are still four routing schedules, while the total minimum routing cost is 4750 RMB. Compared with soft time window, the No.1 route, No.3 route and No.4 route are the same; however the difference is No.2 route, shown in Table 5.

In Table 4, there is a penalty cost of the No.2 route. In order to avoid the penalty, the No.2 route changes its routing schedule in Table 5 (hard time windows). It is clear that this is early penalty, so the improved routing schedule in hard time windows has more distance to avoid early arrival penalty. In this early arrival case, the number of transport vehicle is the same between soft time windows and hard time windows. But, if it is a delay penalty, maybe another transport vehicle should be added to avoid delay penalty and minimize the total cost in hard time times. In the case above, it seems there is only a little cost difference between soft time windows and hard time windows. In fact the cost difference depends on many factors, such as Cej, Pe(t), Pl(t), v and so on. It will vary with the values of these factors. It is possible that there are a large difference between hard time windows and soft time windows. If the penalty cost turns larger, it will be considered to add another transport vehicle to avoid the large penalty cost. Every finished vehicle logistics company can set these factors according to their practice and decide which solution is better.

Table 4 The optimization vehicle routing results (soft time windows)

Table 5 The optimization vehicle routing results (hard time windows)

In order to fully evaluate the proposed algorithm, more experiments are conducted. As the problem size increases, the computational time of the GA algorithm is modest and can work well in practice. In Table 6, there are 100 orders. After a series of tests, the control parameters for the algorithm are set. The population size is 100, crossover probability is 0.7, and mutation probability is 0.2. After 1000 iteration times, the computation results with soft time windows are shown as Fig.1. There are 18 routes and the total minimum routing cost is 20120RMB, shown as follows.

Table 6 Customer orders information

Fig.1 The optimization routes of soft time windows with penalty

The No. 1 Route: 0→70→40→88→67→30→83→0

The No. 2 Route: 0→27→13→55→95→18→74→68→29→0

The No. 3 Route: 0→46→16→2→58→86→72→0

The No. 4 Route: 0→7→36→22→50→66→0

The No. 5 Route: 0→19→42→28→14→17→3→0

The No. 6 Route: 0→47→26→12→51→93→9→0

The No. 7 Route: 0→82→90→76→39→11→53→0

The No. 8 Route: 0→48→34→6→25→81→0

The No. 9 Route: 0→33→78→31→37→23→0

The No. 10 Route: 0→5→73→38→80→52→0

The No. 11 Route: 0→20→32→4→62→60→44→0

The No. 12 Route: 0→41→49→35→77→69→100→0

The No. 13 Route: 0→98→61→59→65→79→0

The No. 14 Route: 0→89→84→57→1→96→0

The No. 15 Route: 0→91→45→87→43→99→85→0

The No. 16 Route: 0→97→63→21→94→10→0

The No. 17 Route: 0→54→56→75→71→15→0

The No. 18 Route: 0→92→64→8→24→0

6 Conclusion

This study addresses a real transportation problem in finished vehicle logistics, and develops a finished vehicle routing model by considering not only the minimum routing cost but also the time windows with penalty function. To test the validity of the proposed genetic algorithm, an example is conducted. From the view of a practical contribution, a method with high performance is developed to simultaneously consider total routing cost of the vehicle fleet, specified geometry restrictions on transport vehicle availability, time windows and penalty function. Moreover, the cost difference depending on penalty factors, transport cost, and transport velocity is compared. In fact maybe there are relative relationships among these parameters. In the future building experience formulation based on these factors will be focused in the finished vehicle routing problem, and schedulers will benefit from it. Other optimization algorithms will be exploved to solve the FVLTW problem, meanwhile the random traffic jam will be considered.

[1] Hopper E, Turton B C H. An empirical study of meta-heuristics applied to 2D rectangular bin packing. Communications of the Acm, 2002, 35(8):66-80

[2] Lesh N, Marks J, McMahon A, et al. Exhaustive approaches to 2D rectangular perfect packings. Information Processing Letters, 2004, 90(1): 7-14

[3] Fuellerer G, Doerner K F, Hartl R F, et al. Ant colony optimization for the two-dimensional loading vehicle routing problem. Computers and Operations Research, 2009, 36(3): 655-673

[4] Leung S C H, Zhou X, Zhang D, et al. Extended guided tabu search and a new packing algorithm for the two-dimensional loading vehicle routing problem. Computers and Operations Research, 2011, 38(1):205-215

[5] Hu Q, Lim A, Zhu, W. The two-dimensional vector packing problem with piecewise linear cost function. Omega, 2014,50: 43-53

[6] Pisinger D, Sigurd M. The two-dimensional bin packing problem with variable bin sizes and costs. Discrete Optimization, 2005,2(2):154-167

[7] Tarantilis C D, Zachariadis E E, Kiranoudis C T. A hybrid metaheuristic algorithm for the integrated vehicle routing and three-dimensional container-loading problem. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(2):255-271

[8] Bortfeldt A. A hybrid algorithm for the capacitated vehicle routing problem with three-dimensional loading constraints. Computers and Operations Research, 2012,39(9): 2248-2257

[9] Iori M, Salazar-González J J, Vigo D. An exact approach for the vehicle routing problem with two-dimensional loading constraints. Transportation Science, 2007,41(2): 253-264

[10] Gendreau M, Iori M, Laporte G, et al. A tabu search heuristic for the vehicle routing problem with two-dimensional loading constraints. Networks, 2008, 51(1):4-18

[11] Moura A, Oliveira J F. An integrated approach to the vehicle routing and container loading problems. OR Spectrum, 2009,31(4): 775-800

[12] Zachariadis E E, Tarantilis C D, Kiranoudis C T. A guided tabu search for the vehicle routing problem with two dimensional loading constraints. European Journal of Operational Research, 2009, 195(3): 729-743

[13] Lai M, Tong X. A metaheuristic method for vehicle routing problem based on improved ant colony optimization and tabu search. Journal of Industrial & Management Optimization, 2012,8(2):469-484

[14] Vidal T, Crainic T G, Gendreau M, et al. Heuristics for multi-attribute vehicle routing problems: A survey and synthesis. European Journal of Operational Research, 2013, 231(1):1-21

[15] Holweg M, Miemczyk J. Logistics in the “three-day car” age: Assessing the responsiveness of vehicle distribution logistics in the UK. International Journal of Physical Distribution and Logistics Management, 2002,32(10):829-850

[16] Mattfeld D C, Kopfer H. Terminal operations management in vehicle transshipment. Transportation Research Part A: Policy and Practice, 2003, 37(5): 435-452

[17] Wu B F, Liu Z Y. A study on finished vehicle logistics in China: Its development trend and resource integration. Automotive Engineering, 2005, 27(3):367-371

[18] Jing L I, Zhang B X. Study on the cause and countermeasures of high-cost finished vehicle logistics in China. Logistics Technology, 2007, 8: 015

[19] Kim J, Ok C S, Kumara S, et al. Amarket-based approach for dynamic vehicle deployment planning using radio frequency identification (RFID) information. International Journal of Production Economics, 2010,128(1):235-247

[20] Tasan A S, Gen M. A genetic algorithm based approach to vehicle routing problem with simultaneous pick-up and deliveries. Computers & Industrial Engineering, 2012, 62(3): 755-761

[21] Baker B M, Ayechew M A. A genetic algorithm for the vehicle routing problem. Computers & Operations Research, 2003,30(5):787-800

Liu Jiansheng, born in 1978. He received his Ph.D degree from Nanchang University in 2009．He studied in Auburn University in USA as a visiting scholar granted by Chinese Scholarship Council. His research interests focus on digital & intelligent manufacturing, facility layout and logistics management and optimization.

10.3772/j.issn.1006-6748.2017.01.008

②To whom correspondence should be addressed. E-mail: dzduan@163.com Received on Sep. 20， 2016

①Supported by the National Natural Science Foundation of China (No. 51565036).