基于Mein-Larson入渗模型的降雨滑坡失稳破坏概率研究
李秀珍, 张小红
(1.中国科学院 山地灾害与地表过程重点实验室, 四川 成都 610041; 2.中国科学院成都山地灾害与环境研究所, 四川 成都 610041; 3.重庆川东南地质工程勘察设计院, 重庆 400038)
基于Mein-Larson入渗模型的降雨滑坡失稳破坏概率研究
李秀珍1,2, 张小红3
(1.中国科学院 山地灾害与地表过程重点实验室, 四川 成都 610041; 2.中国科学院成都山地灾害与环境研究所, 四川 成都 610041; 3.重庆川东南地质工程勘察设计院, 重庆 400038)
[目的] 评价降雨诱发浅层滑坡的失稳破坏概率,为相关研究提供理论依据。[方法] 在引入并扩展了Mein-Larson降雨入渗模型的基础上,将Mein-Larson入渗模型与无限边坡稳定性方法有机结合,建立2种降雨情形(高强度短历时和低强度长历时)下降雨滑坡稳定性的确定性评价模型,然后再将蒙特卡洛数值模拟方法与降雨滑坡的确定性评价模型结合,建立降雨滑坡稳定性的概率评价方法。[结果] 提出了1种降雨诱发浅层滑坡失稳的概率评价方法。[结论] 概率评价方法可以描述降雨滑坡发生及发展过程中存在的不确定性,可以计算不同降雨情形下,不同降雨时刻降雨诱发边坡的失稳破坏概率。该方法的评价结果更符合边坡实际情况。
Mein-Larson入渗模型; 降雨滑坡; 无限边坡稳定性分析方法; 失稳破坏概率
文献参数: 李秀珍, 张小红.基于Mein-Larson入渗模型的降雨滑坡失稳破坏概率研究[J].水土保持通报,2017,37(1):219-223.DOI:10.13961/j.cnki.stbctb.2017.01.039; Li Xiuzhen, Zhang Xiaohong. A study of instability probability of rainfall-induced landslides based on Mein-Larson infiltration model[J]. Bulletin of Soil and Water Conservation, 2017,37(1):219-223.DOI:10.13961/j.cnki.stbctb.2017.01.039
降雨是诱发滑坡活动的一个十分重要的触发因素和动力来源。降雨滑坡在世界上不仅分布广泛,发生频率高,而且给人类造成的危害也十分严重。目前,国内外研究者已提出了许多评价和预测降雨滑坡的理论和方法,如统计分析法和确定性模型法[1]。前者是基于统计分析或试验方法获得的降雨与滑坡之间的相关性规律;后者是基于降雨入渗诱发边坡失稳的物理过程建立相应的物理模型,再利用这些物理模型进行定量评价和预测。众所周知,在降雨滑坡的评价和预测问题中,存在着很多不确定性因素(如岩土体参数内聚力、内摩擦角和渗透系数等),岩土体参数的不确定性直接导致了降雨滑坡发生的随机性和不确定性。不论是统计方法还是确定性模型法,均把这些不确定性的因素当作确定性因素去处理。大量的边坡工程实践也表明,稳定性系数大于1的许多边坡发生了破坏,而稳定性系数小于1的边坡却一直安然无恙。为了有效地考虑这种不确定性,概率分析方法已被逐渐引入到了边坡和滑坡的稳定性分析和评价中[2-8]。但在降雨诱发滑坡的稳定性评价和预测方面,概率分析方法却鲜有研究。目前,仅有极少数研究者对此进行了探索和尝试性研究[6-8]。本文将在引入Mein-Larson降雨入渗模型的基础上,综合考虑高强度短历时和低强度长历时2种降雨情形,并考虑岩土体参数(内聚力和内摩擦角)的随机性,将Mein-Larson入渗模型与基于饱和土的无限边坡稳定性分析方法以及蒙特卡洛方法有机结合起来,来评价降雨诱发浅层滑坡的失稳破坏概率。
1 降雨诱发浅层滑坡的稳定性概率分析方法
1.1 Green-Ampt,Mein-Larson降雨入渗模型
Green和Ampt早在1911年根据毛管理论提出了近似积水模型。该模型是研究初始干燥的土壤在薄层积水时的一维平面入渗问题[9]。由于Green-Ampt模型形式简单,且物理概念清晰,已成为描述垂直入渗过程中应用最为广泛的入渗模型之一。其基本假定是: ① 渗入土壤中的水分从土壤表面至入渗锋面沿深度的水分分布是均匀的,同时是饱和的;② 入渗时存在着明确的水平湿润锋面,将湿润的和未湿润的区域截然分开,湿润区土壤含水量为饱和含水量,未湿润区则为初始含水量。
根据达西定律,可求出地表处的入渗率为[10-11]:
(1)
式中:Ks——土体饱和渗透系数(饱和导水率)(m/h);S——湿润锋平均基质吸力(m);ZW——概化湿润锋深度(m);H——地表积水厚度(m);i——降雨入渗率(m/h)。
由水量平衡原理,可求得累积入渗量I与湿润锋深度Zw的关系为:
(2)
式中:I——累积入渗量(m);θs——饱和含水率(%);θi——初始含水率(%)。下同。
Mein-Larson模型是Mein和Larson于1973年将Green-Ampt模型应用于降雨入渗条件下提出的[12-15]。该模型假定在降雨入渗过程中湿润锋平行向下推进,传导区含水率均匀分布。最初的Mein-Larson模型只考虑了坡面有积水的情形,而且坡面为水平面。根据降雨入渗的基本理论,下面主要分2种情形对恒定降雨条件下经过坡度修正后的Mein-Larson模型进行简要介绍。
(1) 降雨强度p大于土体饱和渗透系数Ks时。
设稳定的降雨强度为p,当p大于土体的入渗能力时,地表才形成积水。假设当累计入渗量达到某一Ip值时,入渗率等于降雨强度(i=p),此时开始积水。因此,可导出开始积水时的累计入渗量Ip值:
(3)
式中:S——湿润锋平均基质吸力(m);M——饱和含水率与初始含水率的差值(%),即M=θs-θi。
积水时间tp为:
(4)
各时段的累积入渗量I为:
(5)
式中:ts——t=0开始积水,到累计入渗量I=Ip时所需要的时间,其计算公式为:
(6)
根据公式(2),可得出湿润锋的竖直入渗深度Zw为:
(7)
(2) 降雨强度p小于土体饱和渗透系数Ks时。
当降雨强度小于土体的饱和渗透系数时,降雨全部渗入土体中。考虑坡度对降雨入渗的影响,则有累积入渗量I为:
I=ptcosβ
(8)
相应地,可得出湿润锋的竖直入渗深度Zw为:
(9)
公式(7)和(8)中的参数同上。
1.2 降雨诱发浅层滑坡的稳定性分析模型
降雨入渗模型与边坡稳定性分析方法有机结合是评价降雨滑坡稳定性的有效方法。无限边坡方法是山区平面滑动型边坡常用的稳定性分析方法。当边坡潜在滑面的深度与边坡长度之比很小时(一般深长比小于0.1时),就可以把该边坡当作一个无限边坡进行分析。将上述Mein-Larson入渗修正模型与无限边坡稳定性分析方法相结合,不但可以考虑坡面倾斜的影响,而且可以同时考虑2种不同降雨形式(低强度长持续时间和高强度短持续时间)下浅层边坡的稳定性随降雨时间的变化情况。
本研究中假定湿润锋以上土体处于饱和状态。Xie等(2004)提出的Green-Ampt模型结合饱和土无限边坡的稳定性分析方法,仅针对降雨强度小于土体饱和渗透系数的情况。本研究拓展和改进了Xie-Tetsuro-Cai提出的模型,将Mein-Larson降雨入渗修正模型和饱和土无限边坡稳定性分析方法有机结合,综合考虑了降雨强度大于土体饱和渗透系数和降雨强度小于土体饱和渗透系数两种情况。主要计算公式如下:
① 降雨强度p大于土体饱和渗透系数Ks时,边坡的稳定性系数Fs为:
(10)
式中:c′——土体有效内聚力(kPa);φ′——土体有效内摩擦角(°);γw——水的重度(kN/m3);γsat——土体的饱和重度(kN/m3);β——边坡的坡角(°);Fs——边坡稳定性系数。
降雨入渗深度zw的计算同公式(7)。
② 降雨强度p小于饱和渗透系数Ks时,边坡的稳定性系数计算公式同式(10),降雨入渗深度Zw的计算同公式(9)。
1.3 降雨诱发浅层滑坡的失稳破坏概率分析
蒙特卡洛法又称随机模拟法或统计试验法,该方法于20世纪40年代首次被提出,是用数学方法模拟具有某种分布的随机变量(如c,φ)的抽样值,以此来解决随机变量的运算问题(如边坡稳定性系数Fs值)[16]。该方法特别适合于已知随机变量的概率密度分布形式或已知随机变量符合某种假定的分布形式,在目前可靠度分析中,是一种相对精确、有效的计算方法。
假定θ表示降雨诱发浅层滑坡稳定性问题中的随机变量,f(θ)表示θ的概率密度函数,Fs(θ,t)表示边坡在降雨时间t的稳定性系数,则边坡在降雨时间t的失稳破坏概率P(t)可以表示为[7]:
pf(t)=∭J〔Fs(θ,t)〕f(θ)dθ
(11)
式中:
根据蒙特卡洛方法,可得边坡的破坏概率为:
(12)
式中:θk——θ的第k个样本;N——样本数目。
将公式(10)和公式(12)结合起来,即可计算不同降雨情形下,在不同降雨时刻降雨诱发浅层边坡的失稳破坏概率。已有研究认为在滑坡失稳概率及可靠度计算中,一般对c和φ等随机变量的抽样达到1 000次即可满足精度要求。因此,本研究中对随机变量的取样次数为1 000次。
2 实例分析应用
选取一坡度为30°的无限边坡进行计算分析。边坡的几何、物理力学性质及水文等参数详见表1。

表1 边坡相关参数取值
本研究中,主要考虑土体内聚力和内摩擦角2个参数的不确定性。假定土体内聚力c′和内摩擦角φ′均符合对数正态分布。c′的均值和方差分别为8,2.4 kPa,φ′的均值和方差分别为30°和3.75°。
2.1 高强度短历时的降雨(降雨强度大于土体饱和渗透系数情形)
当降雨强度p=0.024 m/h,连续降雨12 h。考虑岩土体参数的随机性和不确定性,将蒙特卡洛方法与降雨强度大于土体饱和渗透系数情形下的无限边坡稳定性分析方法〔即公式(10)和公式(7)〕有机结合起来,即可计算该情形下不同降雨时刻边坡的稳定性系数及失稳概率。具体计算结果见图1—4。

图1 降雨入渗深度随降雨时间的变化曲线
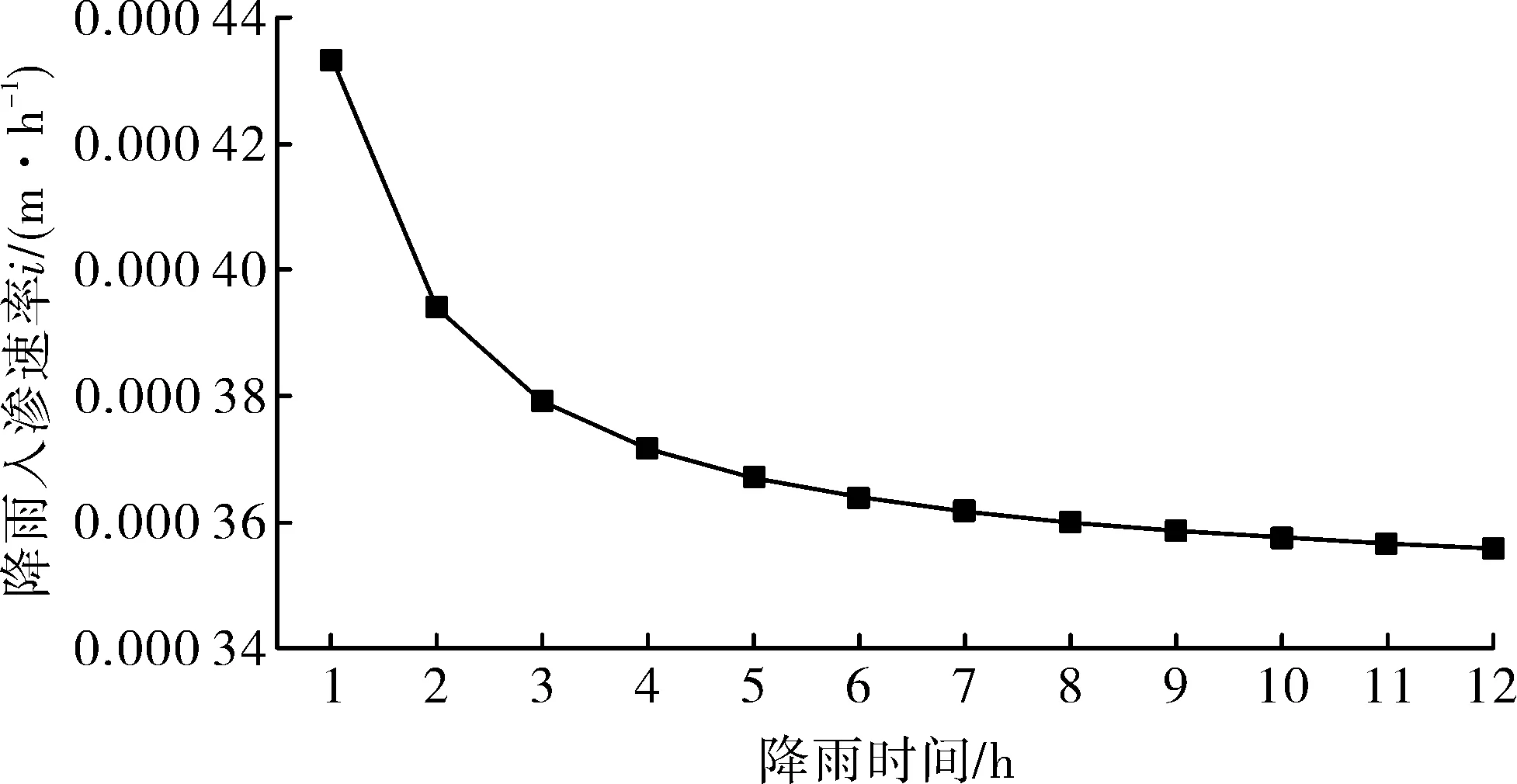
图2 降雨入渗率随降雨时间的变化曲线
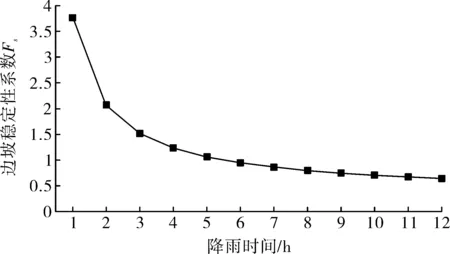
图3 边坡稳定性系数随降雨时间的变化

图4 边坡失稳破坏概率随降雨时间的变化
从图1—4中可以看出,当降雨强度大于土体饱和渗透系数时,降雨入渗速率随降雨时间呈指数函数下降,降雨入渗深度随降雨时间呈线性关系增加。随着降雨时间的延续,边坡的稳定性系数越来越小,失稳破坏概率越来越大。当降雨时间达到5 h后,降雨入渗的深度为1.198 m,边坡的稳定性系数为1.063。此时的边坡处于临界状态,失稳破坏概率为60.9%。
2.2 低强度长历时的降雨(降雨强度小于土体饱和渗透系数情形)
当降雨强度p=0.0068 m/h,连续降雨36 h。考虑岩土体参数的不确定性,将蒙特卡洛方法与降雨强度小于土体饱和渗透系数情形下的无限边坡稳定性分析方法(即公式(10)和公式(9))有机结合起来,即可计算该情形下不同降雨时刻边坡的稳定性系数及失稳概率。具体计算结果见图5—8。

图5 降雨入渗深度随降雨时间的变化
从图5—8可以看出,当降雨强度小于土体饱和渗透系数时,降雨以一恒定入渗速率下渗,降雨入渗深度随降雨呈线性关系增加。随着降雨时间的延续,边坡的稳定性系数逐渐减小,失稳破坏概率逐渐增大。当降雨时间达到19 h后,降雨入渗的深度达到1.299 m,此时,边坡的稳定性系数为1.046,失稳破坏概率为65.1%,边坡处于临界状态。之后,随降雨时间的延续,边坡处于不稳定状态。

图6 降雨入渗率随降雨时间的变化

图7 边坡稳定性系数随降雨时间的变化
3 结 论
由于岩土体参数及降雨诱发因素等的随机性和不确定性,直接导致了降雨滑坡失稳破坏的不确定性。因此对降雨滑坡的稳定性运用概率方法进行分析是十分必要的。本研究中,在引入并扩展了Mein-Larson降雨入渗模型的基础上,将Mein-Larson入渗模型与无限边坡稳定性方法有机结合,建立了2种降雨情形(高强度短历时和低强度长历时)下降雨滑坡稳定性的确定性评价模型,然后又将蒙特卡洛方法与降雨滑坡稳定性的确定性评价模型有机结合,提出了一种降雨诱发浅层滑坡失稳的概率评价方法。典型边坡实例分析结果表明,这种方法理论明确、易于应用,不仅可以描述降雨滑坡发生及发展过程中存在的不确定性,而且可以计算不同降雨情形下,不同降雨时刻降雨诱发边坡的失稳破坏概率,评价结果更符合边坡实际。
[1] 马崇武,刘忠玉.降雨入渗时无限边坡的水平位移与稳定性分析[J].岩土力学,2007,28(S1),563-568.
[2] 徐卫亚,张志腾.滑坡失稳破坏概率及可靠度研究[J].灾害学,1995,10(4):33-37.
[3] Lee S, Pradhan B. Probabilistic landslide hazards and risk mapping on Penang Island, Malaysia[J]. Journal of Earth System Science, 2006,115(6):661-672.
[4] Sivakumar B G L, Murthy D S. Reliability analysis of unsaturated soil slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005,131(11):1423-1428.[5] Cassidy M J, Uzielli M, Lacasse S. Probability risk assessment of landslides: A case study at Finneidfjord[J]. Canadian Geotechnical Journal, 2008,45(9):1250-1267.
[6] Zhang L L, Zhang L M, Tang W H.Rainfall-induced slope failure considering variability of soil properties[J]. Geotechnique, 2005,55(2):183-188.
[7] Zhang J, Huang H W, Zhang L M, et al. Probabilistic prediction of rainfall-induced slope failure using a mechanics-based model[J]. Engineering geology, 2014, 168:129-140.
[8] Melchiorre C, Frattini P. Modelling probability of rainfall-induced shallow landslides in a changing climate, Otta, Central Norway[J]. Climatic Change, 2012,113(2):413-436.
[9] 张光辉,邵明安.用土壤物理特性推求Green-Ampt入渗模型中吸力参数S*f[J].土壤学报,2000,37(4):553-557.
[10] Xie M, Esaki t, Cai M. A time-space based approach for mapping rainfall-induced shallow landslide hazard[J]. Environmental Geology, 2004,46(6):840-850.
[11] 胡立雄,白会人.降雨入渗的边坡稳定评价方法[J].辽宁工程技术大学学报:自然科学版,2007,26(2):235-237.[12] Mein R G, Larson C L. Modeling infiltration during a steady rain[J]. Water Resources Research, 1973,9(2):384-394.
[13] Chen Li, Young M H.Green-Ampt infiltration model for sloping surfaces[J]. Water Resources Research, 2006,42(7):1-9.
[14] Shu Tungchu.Infiltration during an unsteady rain[J]. Water Resources Research, 1978,14(3):61-466.
[15] 李宁,许建聪,钦亚洲.降雨诱发浅层滑坡稳定性的计算模型研究[J].岩土力学,2012,23(5):1485-1490.
[16] 徐钟济.蒙特卡洛法[M].上海:上海科技出版社,1985:10-24.
A Study of Instability Probability of Rainfall-Induced Landslides Based on Mein-Larson Infiltration Model
LI Xiuzhen1,2, ZHANG Xiaohong3
(1.KeyLaboratoryofMountainHazardsandSurfaceProcesses,ChineseAcademyofSciences,Chengdu,Sichuan610041,China; 2.InstituteofMountainHazardsandEnvironment,ChineseAcademyofSciences,Chengdu,Sichuan610041,China; 3.ChongqingGeologicalEngineeringInvestigationandDesignInstituteofSoutheastSichuan,Chongqing400038,China)
[Objective] The objective of the study is to evaluate the instability probability of shallow landslide induced by rainfall, and to provide theoretical basis for related research. [Methods] We combine Mein-Larson model with infinite slope stability models of saturated soil by introducing and developing the Mein-Larson infiltration model, and establish deterministic models for rain-induced landslides under short duration rainfall with high intensity and long duration rainfall with low intensity. Then we establish a probability analysis method of the slope instability by combining the deterministic models with Monte Carlo method. [Results] One kind of evaluation method for the failure probability of shallow landslide induced by rainfall was proposed.[Conclusion] The probability method not only can describe the uncertainties in the process of occurrence and development of rain-induced landslides, but also can calculate the instability probability of rain-induced slope instability under the different rainfall time. The assessment results are in high agreement with the actual slope.
Mein-Larson infiltration model; rainfall-induced landslides; infinite slope stability analysis method; instability probability
2016-04-27
2016-06-12
中国科学院重点部署项目子课题“泥石流动力过程及调控模拟”(KZZD-EW-05-01-02); 国家重点基础研究发展计划(973计划)(2015CB452704,2013CB733205)
李秀珍(1975—),女(汉族),内蒙古自治区乌盟人,博士,副研究员,硕士生导师,主要从事地质灾害评价与预测等方面的研究。E-mail:lxzljt@sina.com。
B
1000-288X(2017)01-0219-05
P642.22

