基于地形剖面线的陕北黄土高原地貌信息熵差分析
殷宗敏, 刘万青
(1.西北大学 城市与环境学院, 陕西 西安 710127; 2.兰州大学 资源环境学院, 甘肃 兰州 730000)
基于地形剖面线的陕北黄土高原地貌信息熵差分析
殷宗敏1,2, 刘万青1
(1.西北大学 城市与环境学院, 陕西 西安 710127; 2.兰州大学 资源环境学院, 甘肃 兰州 730000)
[目的] 计算黄土高原地貌评价指标和剖面上高程数据信息熵,用以拟合地形起伏,评价地形,为地貌研究提供新理论依据。[方法] 通过对研究区域进行剖面分析,获取地形剖面线,利用高程数据计算不同地貌类型中剖面线信息熵,绘制地形剖面线图和地形剖面线信息熵图,用来检验和评价地貌信息熵对地形的表达效果,统计两者离散程度指标,通过线性拟合找出两者相关性指标。[结果] 将两图进行对比分析,发现两图走势具有一定的相似性,采用统计指标作为指示器,结果表明高程曲线与信息熵曲线具有较强的相关性,采用侵蚀模数验证,表明信息熵在表示地貌起伏或侵蚀方面具有可靠性。[结论] 地貌信息熵可以用来模拟地形,且模拟效果良好,可以用于评价地貌类型。
黄土高原; 地形剖面线; 信息熵; 对比分析
文献参数: 殷宗敏,刘万青.基于地形剖面线的陕北黄土高原地貌信息熵差分析[J].水土保持通报,2017,37(1):166-172.DOI:10.13961/j.cnki.stbctb.2017.01.030; Yin Zongmin, Liu Wanqing. Information entropy difference analysis based on terrain profile line of Loess Plateau in Northern Shaanxi Province[J]. Bulletin of Soil and Water Conservation, 2017,37(1):166-172.DOI:10.13961/j.cnki.stbctb.2017.01.030
地形起伏作为地理学研究的一个方向,对于区域规划、生态修复、水土保持等具有重要价值。黄土高原作为一个独特的区域,长期受到专家学者的重视,对于其地形起伏特征的研究已有多种方法[1]。主要从遥感影像表面纹理或者单纯、离散的高程数据来进行分析;如果地形起伏研究从多组内部平行剖面线开始,将提供一种崭新的研究思路。
香农的信息熵理论,是用于度量信息量的概念,用来评价信息量的多少。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高[2]。对于黄土地貌而言,若侵蚀状态轻微,则表现为表面较平坦,无明显沟壑,为一种有序的状态,故计算所得信息熵较小;反之,若侵蚀严重,则表面崎岖,沟壑纵横,表现为一种无序的状态,故计算所得信息熵较大。由此可见,信息熵在评价地貌类型方面具有价值。若区域面内侵蚀严重,地面起伏则明显,即高程变化剧烈,因此信息熵与高程变化有关;对于评价高程变化,可引入剖面起伏度的概念。定义为剖面线上波峰(波谷)的高程和位于其两侧的波谷(波峰)高程均值之差[3]。
对于剖面线而言,其有序的高程数据按照剖面线走向依次排列,根据地理学第一定律,相邻事物间具有强相关性,可知:有序的高程信息蕴含一定信息量,而信息量可以通过信息熵来度量。因此,对地形剖面线上高程数据计算信息熵理应反映地形起伏变化,即地形起伏。通过对剖面上高程数据计算信息熵,能够拟合地形起伏,评价地形[4]。因此本文从该角度出发,做一些有意义的尝试。
对于地形特征的评价指标,现有的评价参数如下。① 坡面地形因子:坡面姿态因子、坡形因子、坡长因子、坡位因子、坡面复杂度因子。② 特征地形要素:地形特征点、山脊线、山谷线、沟沿线、水系、流域[5]。③ DEM地形统计分析:相关分析、回归分析、趋势面分析。④ DEM地学模型分析:以DEM为对象构建模型[6]。本文创造性的引入了信息熵的概念,对于信息熵的研究,有3种常用方法: ① 概率统计方法,直接来自香农公式,忽略了地物间的强相关性; ② 组合的方法,这是建立在地物表面构成元素多元的基础上的方法,不具有具体计算的功能[7-8]。③ 综合特征值量测法,公式为:
i=lg(1+w)
(1)
式中:w——制图特征[7];i——信息熵(hart,以10为底)。
本文拟以该公式为基础,对其进行适当修改后,用于计算地形剖面线的信息熵,并借此反映地形起伏状态[8]。
1 数据与方法
1.1 数据来源及预处理
通过数据共享平台(STRM 下载地址:http:∥srtm.csi.cgiar.org/SELECTION/inputCoord.asp),获得黄土高原地区的数字高程模型,数据格式为GRID,坐标系统为WGS_1 984,高程最小值为93 m,最大值为4 981 m,平均高程为1 408 m。矢量化陕西省内黄土高原地区的不同地貌类型分区图。鉴于地貌分区图图斑数量较多,且大小不一,如果统一采样间距时兼顾各图斑,将明显限制采样间距长度,影响结果表达;因此采用取舍的思路,选取面积较大、长宽比接近1的区域,符合该条件的区域有10个,分别为:残塬沟壑、高塬沟壑、黄龙山低山丘陵沟壑、宽梁残塬沟壑、梁峁丘陵沟壑、梁状丘陵沟壑、峁梁丘陵沟壑、峁状丘陵、破碎塬沟壑、沙丘草滩沙地。对这10类区域的DEM数据做高程3 D分析,绘制剖面图,剖面线采用平行线采样法绘制,选取合适位置的6组相同长度的剖面线所得高程的平均值作为最终采样线,获得该采样线的高程数据[9]。
1.2 分析方法
信息熵是一个数学上颇为抽象的概念,理解为某种特定信息的出现概率[10]。将信息熵应用于地理学,其蕴含了地物所具有的信息,反映为地物的评价指标。由于地物在空间格局上表现为极强的相关性,该相关性反映了制图特征;所以在应用公式(1)时,w应反映出地物间的相关性,文中地物表现为高程数据,因此w中应蕴含相邻采样点间高程的对应关系,故引入剖面起伏度的概念,用A表示,其为剖面线上波峰(波谷)的高程和位于其两侧的波谷(波峰)高程均值之差[2]。剖面线表现为线状要素,其信息量取决于构成线要素的节点在表达要素整体形态上的重要性程度。若重要性程度越高,则信息量越大[11]。如何评价重要性程度的高低,根据邓敏等[11]的研究成果,可以对节点拟定一个半径绘制圆,与节点相邻两边有交点,将节点到两交点连线的垂距除以两交点间距离,所得比值为重要性程度,比值越大则重要性程度越高。

(2)
式中:A——起伏度;d——采样间距(m);i——地貌信息熵(Hart)。
信息熵反映的是地形的变化程度,不具有区分正负地形的作用。广义的正地形指的黄土高原区域相对于周边地区明显高出的区域,负地形指的是相对凹陷的区域[12]。信息熵计算的结果始终为正值,对于正地形部位或者负地形部位变化程度相同的地貌类型,所得的信息熵值可能相等,为了更好区分这两类地貌,引入系数k:
(3)

将预处理得到的陕北不同地貌类型的DEM数据与陕北黄土地貌分区图叠加显示。使陕北黄土地貌分区图在DEM数据的上层,并在该层上绘制剖面线[9],剖面线的绘制方法采用创建渔网方式,对渔网绘制赋予高程信息;同时利用线裁剪方式获得6组平行线,顾及到地貌走向,选取的平行线位置大致居中分布,平行线线长36 km,线间间距为2 km,利用平行线,绘制剖面图;出于对比考虑,选取横纵走向2种剖面线。利用ArcGIS软件,获得高程数据,通过Excel的函数功能,利用上文的计算公式计算剖面线的信息熵。
利用获得的数据,分别绘制地形剖面线图和地形剖面线信息熵图,并且将两图进行对比分析,获得结论,并对分析结果进行可靠性验证。
至于区域图斑中采样间距的确定,综合考虑2个因素:一是研究区的空间尺度大小(一般尺度越大,则间距越大;反之亦然)。二是地貌单元的空间规模(规模越大,则间距越大;反之亦然)[13]。最终确定采样线采样长度为36 km,平行采样线间间距为2 km,采用该尺度,能够使得在指定区域图斑中横向、纵向都能采样,保证了数据的完整性,可以研究地形走向对计算所得信息熵的影响。图1为分析方法的技术流程。
2 结果与分析
2.1 试验结果
对陕北黄土地区的10个样区,选择横纵走向的剖面线,进行相应的处理,计算信息熵,由于信息熵计算结果为较小的小数,因此对结果乘以系数10 000,扩大其表现效果。利用获得的地形剖面线高程数据,绘制地形剖面线图;利用获得的信息熵数据,绘制出地形剖面线信息熵图。计算各研究地貌的高程、信息熵标准差,并将两者绘制于同一表中(表1),方便进行对比分析。

图1 分析方法技术流程

地貌类型信息标准差横向采样纵向采样高程/m信息熵/hart高程/m信息熵/hart沙丘草滩沙地26.3806.07742.9208.400峁状丘陵32.23250.93424.43450.645峁梁丘陵沟壑63.61270.66432.04263.482残塬沟壑41.38252.71743.86054.762梁状丘陵沟壑41.56872.58828.53754.169梁峁丘陵沟壑55.71663.84243.34665.562宽梁残塬沟壑63.03255.73680.06178.097破碎塬沟壑54.48560.03371.58377.859高塬沟壑84.20368.13549.42954.950黄龙山低山丘陵沟壑160.83967.236121.90397.531
由于原始采样数据中采样点较多,在Excel中用图表绘制时,剖面线起伏过于剧烈,不适合用于规律分析。综合区域内数据特性,选取一定间距采样点数作为移动平均单位,使得图表中波形平滑易于分析,对比发现,采取10个采样点数作为移动平均的单位,能够达到不错的效果。
标准差是总体各单元标准值与其平均数离差平方的算数平均数的平方根。可以反映组内个体间的离散程度。分别统计,高程和信息熵数据中标准差,观察表1中高程和信息熵的标准差,发现高程和信息熵具有对应关系,大致表现为,高程的标准差越大,对应信息熵的标准差也增大,反之亦然;因此推断,高程和信息熵存在明显相关,找出评价指标。在Excel中以高程为横轴,信息熵为纵轴,绘制散点图,并采用多项式拟合绘制趋势线,多项式系数选取6,并显示R2,结果见表2。

表2 高程曲线与信息熵曲线的R2值
对比研究表2中的R2值,可得出如下分析结果:① 无论横向、纵向采样,高程曲线与信息熵曲线的R2值均大于0.8,说明高程与信息熵具有强相关性;② 对比表2中同种地貌类型的R2值,值的大小说明信息熵曲线与高程曲线的拟合程度,拟合程度越高,R2值越大,R2值大的采样方向为合理的采样方向,即地形走向与该采样方向一致; ③ 除黄龙山低山丘陵沟壑应采取纵向采样外,其余地貌采样方式横向更为合适。
在分析过程中也发现了几个值得深入讨论的问题: ① 绘制剖面线时,不同区域内采样线长度相等,然而在不同区域中,采样线的长度占区域的比例不同,其是否影响剖面线对地貌的表达? ② 表2中R2值太大,是否存在偏高的现象,偏高的原因需要探究; ③ 高程和信息熵的标准差的对应存在突变情况,即高程的标准差大时,信息熵的标准差反而小,其原因是什么?
2.2 结果分析
对比地形剖面线图2—3,可得出如下分析结果:
(1) 地形剖面线波形与地形剖面线信息熵波形的走势具有相似性,波形波峰和波谷有对应关系。
(2) 单点高程高时,信息熵可能小,如:残塬沟壑和高塬沟壑;当然信息熵也可能大,如:高塬沟壑和梁状丘陵沟壑。从而反映出信息熵与单点高程值无直接的对应关系,然而从图2—3可以看出信息熵与起伏度有关。
(3) 同种地貌类型其横纵剖面线形态存在差异,同一区域横纵剖面线上平均高程大致相同。
(4) 横向采样的标准差和平均绝对偏差大于纵向采样时,说明横向起伏程度大于纵向起伏程度。
(5) 高程的标准差越大,对应的信息熵的标准差也越大。
2.3 结果检验
为了验证信息熵,在表示地貌起伏或侵蚀方面的可靠性,可选择侵蚀模数来验证,查询资料得知,黄土高塬沟壑区侵蚀模数(1955—2007年平均值)为5 076.7 t/(km2·a),表示强度侵蚀;残塬沟壑区侵蚀模数(1955—2007年平均值)为8 769.4 t/(km2·a),表示强烈侵蚀[13]。观察试验中残塬沟壑和高塬沟壑的绝对值平均信息熵,发现残塬沟壑的绝对值平均信息熵大于高塬沟壑的绝对值平均信息熵,运用引言中的理论,信息熵越大,表明地形起伏越明显,土壤侵蚀越强烈,该试验中的信息熵与资料中的侵蚀模数相贴合,说明该参数在判别地貌类型上具有一定价值。
3 讨论与结论
3.1 讨 论
文中在采样区域内选择线性剖面数据来计算信息熵,如果利用长条带状的方式进行数据采样,计算每个小方块中的平均高程数据,代替剖面线中的点状数据,更能说明区域特征[14]。
对于一种地貌类型,其地形剖面线中高程越大,地形剖面线的信息熵反而越小,可能的解释是,对于正地形而言,更容易发生重力侵蚀,表现为整体性平移,如滑坡,对于负地形而言,更容易发生水力侵蚀,如沟蚀,使得大地被切割的支离破碎[15]。重力导致的侵蚀,造成的黄土地区破碎程度不如水力侵蚀,故信息熵小。
3.2 结 论
由于地形复杂,如果单纯从高程出发,将掩盖地形的其他特征指标,而信息熵的运用,弱化了高程的影响,使得地形表达趋于全面。根据图2—3和表2,并结合结果检验中的检验数据,得出信息熵指标在模拟和评价地形方面具有可靠性,与参考文献[16]一致,大多数情况下两折线的峰值、谷值分别对应,且计算的两者的R2数大于0.8,说明高程与信息熵具有强相关性,所以得出结论,信息熵可以用来模拟地形,且模拟效果良好。

图2 横向剖面线高程和信息熵对比
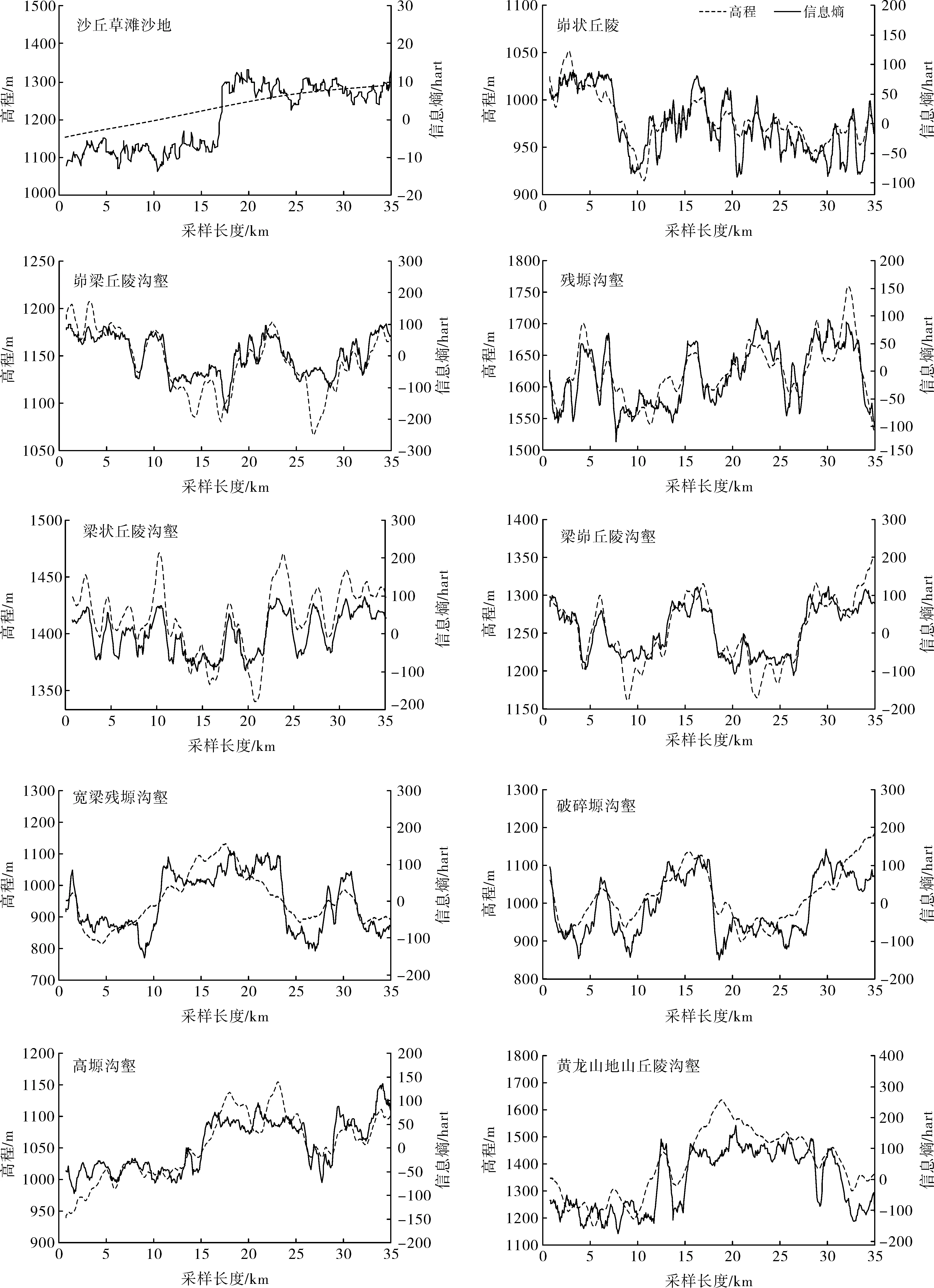
图3 纵向剖面线高程和信息熵对比
致谢:本文在写作过程中,使用的数据包括STRM数据平台的DEM数据,以及甘枝茂先生的黄土高原地区地貌分区图。在此一并表示衷心感谢!
[1] 李炳元,潘保田,程维明,等.中国地貌区划新论[J].地理学报,2013,68(3):291-306.
[2] Shannon C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001,5(1):3-55.
[3] 张维.基于DEM的陕北黄土高原流域剖面谱研究[D].南京:南京师范大学,2011.
[4] 张会平,刘少峰.利用DEM进行地形高程剖面分析的新方法[J].地学前缘,2004,11(3):226-226.
[5] 郭兰勤,丑述仁.基于DEM不同路径算法的沟壑密度提取[J].地下水,2011(6):145-147.
[6] 张磊,汤国安,李发源,等.黄土地貌沟沿线研究综述[J].地理与地理信息科学,2012,28(6):44-48.
[7] 张法.地图信息量的量测和评价[J].测绘,2006,29(1):21-24.
[8] Zhilin Li, Peizhi Huang. Quantitative measures for spatial information of maps[J]. International Journal of Geographical Information Science, 2002,16(7):699-709.
[9] 汤国安. ArcGIS地理信息系统空间分析实验教程[M].北京:科学出版社, 2012.
[10] Peters S. Interactive scale-dependent multidimensional point data selection using enhanced polarization transformation[J]. Journal of Dental Research, 2011,81(4):253-258.
[11] 邓敏,樊子德,刘慧敏.层次信息量的线要素化简算法评价研究[J].测绘学报,2013,42(5):767-773.
[12] 罗来兴.划分晋西、陕北、陇东黄土区域沟间地与沟谷的地貌类型[J].地理学报,1956,22(03):201-222.
[13] 王万忠,焦菊英,马丽梅,等.黄土高原不同侵蚀类型区侵蚀产沙强度变化及其治理目标[J].水土保持通报,2012,32(5):1-7.
[14] 邹斌文,马维峰,龙昱,等.基于ArcGIS的条带剖面提取方法在地貌分析中的应用[J].地理与地理信息科学,2011,27(3):42-44.
[15] 张翼.黄土高原丘陵沟壑区土壤侵蚀研究[J].水土保持研究,2000,7(2):121-124.
[16] 管华.秦岭—黄淮平原交界带地貌信息熵分析[J].河南大学学报:自然科学版,1996,26(4):67-71.
Information Entropy Difference Analysis Based on Terrain Profile Line of Loess Plateau in Northern Shaanxi Province
YIN Zongmin1,2, LIU Wanqing1
(1.CollegeofUrbanandEnvironmentalSciences,NorthwestUniversity,Xi’an,Shaanxi710127,China; 2.CollegeofEarthEnvironmentalSciences,LanzhouUniversity,Lanzhou,Gansu730000,China)
[Objective] This paper studies the geomorphic types from the perspective of information entropy and adds new index for landscape evaluation in Loess Plateau. The terrain can be fitted and evaluated by calculating the information entropy on the elevation data, which can provide a new theoretical basis for studying geomorphology. [Methods] Through analyzing terrain profile of the study area, we extracted the terrain profile line, then used elevation data to calculate the section line information entropy and elevation for different physiognomy types. We rendered terrain profile section line map and terrain information entropy diagram, and used them to test and evaluate the effect of geomorphic information entropy in expressing terrain information, and to calculate the index of dispersion degree, and to find the correlation between them through linear fitting. [Results] With a comparison of two charts, the two figures showed similar trends. The statistical indicators that there was a strong correlation between the elevation curve and the information entropy curve. The validation by erosion modulus showed that the information entropy was reliable in representing the topographic changes or erosion.[Conclusion] Terrain information entropy can be used to simulate the terrain, and the simulation results are farorable, it can be used to evaluate the landscape types.
Loess Plateau; terrain profiles; information entropy; comparison analysis
2016-06-03
2016-06-27
国家自然科学基金项目“地表坡度的统计分布理论模型研究”(41371274)
殷宗敏(1992—),男(汉族),江西省九江市人,硕士研究生,主要研究方向为地貌信息熵及分形分维。E-mail:2267662868@qq.com。
刘万青(1965—),男(汉族),陕西省渭南市人,硕士,副教授,主要从事土壤侵蚀与水土保持等方面的研究。E-mail:liuwqing@nwu.edu.cn。
B
1000-288X(2017)01-0166-07
P931.6

