泥浆对黏性碎屑流坡面运移过程的影响
季宪军, 梁 瑛, 潘华利, 欧国强
(1.南阳理工学院, 河南 南阳 473004; 2.中国科学院 成都山地灾害与环境研究所, 四川 成都 610041)
泥浆对黏性碎屑流坡面运移过程的影响
季宪军1, 梁 瑛1, 潘华利2, 欧国强2
(1.南阳理工学院, 河南 南阳 473004; 2.中国科学院 成都山地灾害与环境研究所, 四川 成都 610041)
[目的] 分析泥浆对黏性碎屑流坡面运动形态、横向宽度、纵向运动距离及运动速度影响,为此类灾害防治提供参考。[方法] 制作黏性碎屑流实验模型,将不同含水率成都黏土泥浆与粗颗粒混合,制备黏性碎屑流试样,开展系列黏性碎屑流物理模型试验。[结果] 随泥浆密度增大,粗颗粒间粘连作用增强,其运动形态由无黏碎屑流向黏性碎屑流再到整体块状运动形态转变;坡面横向宽度、纵向运移距离和速度随泥浆密度增加而减小;不同密度泥浆组成黏性碎屑流运动过程具有分类现象:密度低于1.413 g/cm3时,速度随时间增长快,变化梯度较稳定;密度大于1.413 g/cm3时,运动速度变化过程可分为2个阶段:前期速度随时间增长慢,变化梯度较小;后期速度随时间增长快,且较前阶段变化梯度有所增大,各高密度泥浆情况趋于一致。[结论] 泥浆影响黏性碎屑流运移形态和运动过程。
黏性碎屑流; 运动形态; 模型试验; 泥浆
文献参数: 季宪军, 梁瑛, 潘华利, 等.泥浆对黏性碎屑流坡面运移过程的影响[J].水土保持通报,2017,37(1):088-092.DOI:10.13961/j.cnki.stbctb.2017.01.016; Ji Xianjun, Liang Ying, Pan Huali, et al. Influence of mud on migration process of viscous debris flow[J]. Bulletin of Soil and Water Conservation, 2017,37(1):088-092.DOI:10.13961/j.cnki.stbctb.2017.01.016
崩塌、滑坡是常见山地灾害,降雨是诱发崩塌滑坡灾害主要因素之一,边坡土体失稳后的运移过程中,水与细颗粒土混合形成泥浆,泥浆与无粘粗颗粒混合,以黏性碎屑流形式沿坡面运移,给国家和人民财产造成严重破坏[1-3]。因其具有长距离高速运移和冲击集中,冲击力大及破坏严重等特征,受到社会及国内外从事地质灾害研究者广泛关注[4-7]。对其运动过程研究成为此类灾害控制的关键环节,研究方法主要有数值模拟[8-10]和物理模型试验。因物理模型试验具有良好的直观性而多为研究者所采用。如左自波等[11]探讨含了石量对土坡破坏模式具有显著的影响。周中等[12]分析了土石混合体边坡在降雨入渗作用下的形成条件、变形位移特征及破坏滑移规律;刘波等[13]以三峡库区某滑坡为例,通过物理模型试验探讨库水位变化对该滑坡稳定性的影响。吴火珍等[14]运用非饱和土力学方法,分析了滑坡体在降雨条件下的动态稳定性特征;李焕强等[15]开展模型试验,分析了降雨入渗作用下边坡形状的变化规律;尹洪江等[16]在室内构建泥石流源区松散堆积土体斜坡模型,分析了不同降雨强度下斜坡土体流失规律与斜坡的失稳方式。
以上多是对其失稳机制、变形和破坏模式进行研究,对其失稳后的运动过程研究较少,特别是泥浆对其运动过程影响未见相关文献报道。泥浆作为黏性碎屑流的基本组成,泥浆与粗颗粒相互作用,泥浆对粗颗粒的粘连作用影响黏性碎屑流坡面横向纵向范围,探讨泥浆对其运动过程的影响,对此类灾害防治具有重要的工程意义。为深入分析泥浆对黏性碎屑流运动过程的影响,本文拟以不同密度泥浆与固定组成粗颗粒混合组成的黏性碎屑流,开展黏性碎屑流物理模型试验,用摄像机记录其运移过程,分析泥浆对
黏性碎屑流坡面运动形态、运移速度的影响,以期为此类灾害的防治提供参考。
1 材料与方法
1.1 试验材料
崩滑土体组成复杂,一般具有多组分、宽粒径等特点,且同类别土体的力学性质受含水量影响较大。根据本文的研究目的,旨在探索泥浆对黏性碎屑流运动过程的影响,选用成都市龙泉区黏土(又称成都黏土)作为黏性碎屑流粗颗粒间的泥浆。成都黏土(Q3eol),棕黄、褐黄、灰黄等色,自由膨胀率为40%~72%,液限为38%~50.6%,蒙脱石含量M=13.29%~39.55%,属弱—中等膨胀土,厚5—15 m。野外取样(黏土),经晾干、磨细等过程,试验测定其颗粒组成(表1)及液塑限。液限含水量wL为66.5%,塑限含水量wP为24.5%。塑性指数IP为:
IP=wL-wP=42, >17
(1)
泥浆样品制备:取成都黏土土样若干,加水浸泡,软化土样,测定其密度。取软化后土样若干放置量杯内,分别向杯内加水配制不同密度的泥浆,制备的泥浆试样,各试样编号、密度和含水率见表2。粗颗粒为粒径1~2cm的卵石。用不同含水量的黏土(泥浆)与粗颗粒混合,形成由粗颗粒与黏土组成的黏性碎屑流。

表1 成都黏土颗粒组成

表2 泥浆密度与含水率
1.2 试验模型和方法
物理试验模型主要由积土槽、滑动面、堆积面组成。土样宽度为0.2 m,积土槽出口位置到水平堆积面的y向距离为1.5 m,垂直高度1.0 m。滑动面坡度约为34°,堆积面水平。在堆积面的末端和滑动面侧面各安放1台摄像机,堆积面末端摄像机距堆积面的垂直距离为0.5 m。滑动面侧面摄像机距堆积面的垂直距离为0.5 m。
倾斜滑动面和堆积面以10 cm的方格划分,用以标定黏性碎屑流运动过程中的横向宽度和纵向位置。在滑动面的一侧,放置于滑动面垂直的竖向高度标尺,记录黏性碎屑流运动过程中的竖向厚度。将制备泥浆与粗颗粒掺混,形成黏性碎屑流试样,将掺混料装入一定体积的积土槽内并放置在指定高度位置,准备试验。
对于每种密度的泥浆和粗颗粒组成的黏性碎屑流,在进行试验前,向滑动面和堆积面上撒稀性泥浆水,以尽可能保证在不同试验时,滑动面和堆积面的摩擦系数相等。试验过程中,在堆积面的前端和倾斜滑动面的侧面放置摄像机,记录黏性碎屑流运动过程形态,用于黏性碎屑流运动过程分析。
2 结果与分析
2.1 泥浆对黏性碎屑流运动过程的影响
摄像的起始时间为积土槽前挡板撤去后开始计算,终止时间为黏性碎屑流在堆积面运动停止时。根据分析需要,对录制正面、侧面视频资料进行解译。根据摄像记录不同泥浆情况下黏性碎屑流沿坡面运动过程,截取不同工况下黏性碎屑流侧面形态随时间变化过程(以每5帧为间隔,侧面图像省略)进行对比(图1),分析泥浆对黏性碎屑流运动过程的影响。
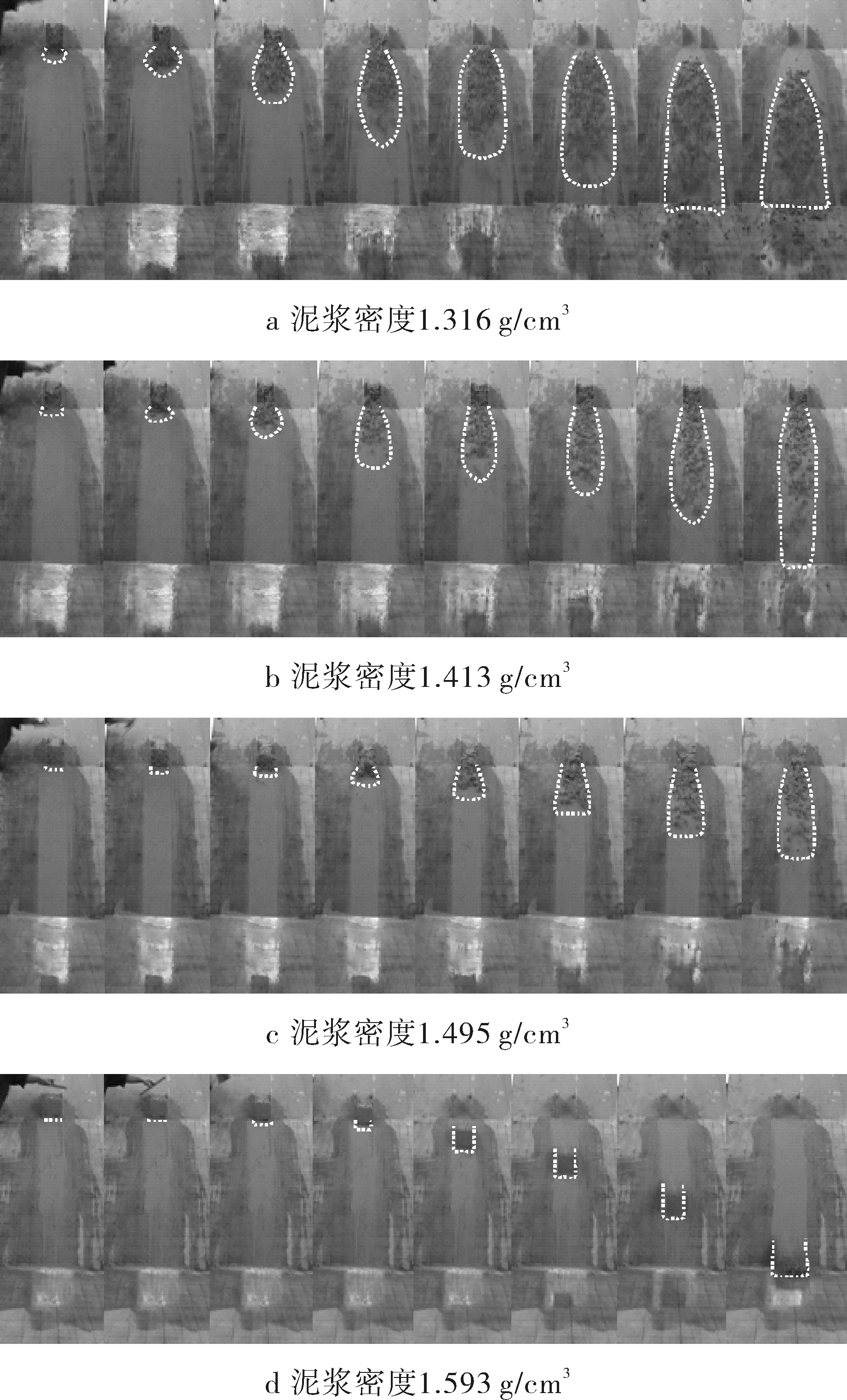
图1 泥浆对黏性碎屑流运动过程的影响正面形态对比
图1表明,泥浆密度不同,黏性碎屑流运动形态存在较大差异,泥浆黏性碎屑流运动形态和运动速度影响明显:密度小,粗颗粒间的粘连作用弱,对崩滑粗颗粒运动影响小,与无粘碎屑流运动类似;随泥浆密度增大,粗颗粒间的粘连作用增强,对运动过程影响不容忽略,运动形态变为黏性碎屑流运动(颗粒碰撞和粘连),最终演变为颗粒不分离的整体块状沿坡面的滑移运动。因此,随泥浆密度增大,其运动形态由无粘碎屑流运动逐渐向黏性碎屑流运动到整体块状运动转变。
2.2 泥浆密度对坡面形态演化过程影响
根据模型试验摄像记录结果,分析不同帧位黏性碎屑流坡面横向宽度和纵向坡面位置,分析泥浆密度对黏性碎屑流坡面运动过程的影响(图2)。

图2 黏性碎屑流坡面运动形态随时间变化过程
图2表明,同一泥浆条件下,黏性碎屑流在重力作用下,其坡面横向展宽和纵向长度随时间的增长而增大,但增大幅度随泥浆密度的增加逐渐减小;黏性碎屑流的坡面展宽和纵向长度随泥浆密度的增大而减小,即密度大,黏性碎屑流运动坡面展宽和长度小,密度小,坡面展宽和长度大。密度越大,其切向剪切应力和法向的粘连力越大,从而对黏性碎屑流运动纵向和横向发展抑制作用越强,对运动过程影响越显著。
2.3 同一时刻黏性碎屑流运动坡面形态对比
根据物理模型试验结果,对比分析不同泥浆情况下黏性碎屑流的坡面形态。为分析泥浆对运动形态的影响,选择在撤除前挡板后第25帧,距前挡板70 cm位置的坡面形态进行对比(坡面横向宽度、纵向长度及与沿滑动面垂直厚度值,见图3—4)。

注:泥浆密度大于1.452 g/cm3后,以整体形式沿坡面运移,但还没运移到相应位置,所以没有厚度。图3 第25帧不同泥浆密度黏性碎屑流坡面尺寸对比
图3—4表明,当泥浆密度较小时,泥浆对颗粒运动约束和抑制作用较弱,当积土槽挡板撤除后,槽内粗颗粒迅速沿坡面下泄,在第25帧(1 s),在坡面中部展开,其横向宽度、纵向距离及竖向厚度较大。泥浆密度较大(大于1.413 g/cm3)时,对粗颗粒的抑制作用增强,限制黏性碎屑流坡面发展,在第25帧(1 s),在未运移至坡面中部,其竖向厚度较小甚至为0。
2.4 泥浆密度对运动距离影响
不同密度泥浆条件下,黏性碎屑流坡面演进位置与时间关系见图5。

图4 第25帧不同泥浆密度黏性碎屑流坡面形态对比

图5 泥浆运动位置与时间的关系
图5表明,同一时刻,由低密度泥浆组成的黏性碎屑流运动距离较低密度泥浆组成的黏性碎屑流运动位置远,并随泥浆密度的增大,其在滑动坡面的运移距离逐渐减小。
2.5 泥浆密度对运动速度影响
图1证实不同密度泥浆影响下的黏性碎屑流坡面形态存在很大的差异,运动形态由颗粒的碰撞运动(颗粒流)向整体块状滑移运动转变;为进一步分析泥浆对黏性碎屑流运动速度的影响,通过试验摄像记录,分析不同泥浆情况下黏性碎屑流坡面纵向运动距离不同,计算其运动速度。并分析泥浆密度对运移速度的影响。采用如下办法确定黏性碎屑流运动速度:
从撤去积土槽前挡板开始为计时帧位,记录不同帧位时黏性碎屑流在坡面的最前端位置(根据滑动面以标记的10 cm×10 cm网格粗略估计)。相邻两次记录位置差值(li-li-1)与相应帧位差值(ti-ti-1)的比值即为该时刻(帧位)黏性碎屑流运动速度。黏性碎屑流前端运动至坡脚位置停止计时。
速度计算公式为:
不同密度泥浆条件下,黏性碎屑流坡面演进速度与时间关系见图6。

图6 黏性碎屑流运动速度—时间关系
图6表明,在同一时刻,密度越大,运动速度越小,最大速度随密度的增大而减小。速度随时间变化情况存在分类现象:密度低于1.413 g/cm3时,速度随时间增加较迅速,且变化梯度较稳定;密度大于1.413 g/cm3时,运动速度变化梯度大致可分为2个阶段:前期速度随时间的变化梯度较小;之后速度随时间变化梯度有所增大,但各高密度情况下趋于一致。
3 结论与讨论
(1) 随泥浆密度增大,粗颗粒间的粘连作用增强,对黏性碎屑流运动形态和运动速度影响明显,其运动形态由无粘碎屑流运动逐渐向黏性碎屑流运动到整体块状运动转变;
(2) 黏性碎屑流坡面横向宽度、纵向运移距离和运动速率随泥浆密度的增加而减小。
(3) 根据纵向位置和速度随时间变化情况,其不同密度泥浆组成黏性碎屑流运动过程具有分类现象:密度低于1.413 g/cm3时,速度随时间的变化梯度较稳定;密度大于1.413 g/cm3时,运动速度变化梯度大致可分为2个阶段:前期速度随时间的变化梯度较小;之后速度随时间变化梯度有所增大,但各高密度情况下趋于一致。
另外,本模型试验仅以不同密度成都黏土作为泥浆,分析其对黏性碎屑流运动过程的影响,而具体崩滑灾害其物质组成极其复杂,需根据其物质组成做具体分析。再者本文根据黏性碎屑流运动位置和速度分析结果,在泥浆密度为1.413 g/cm3时,速度、位置变化过程存在分类现象,但此密度值绝非是不同运动类别阈值;其内在力学机制复杂,可能与坡度、崩滑体物质组成等有关,有待于做进一步研究。
[1] 许强,黄润秋,殷跃平,等.2009年6·5重庆武隆鸡尾山崩滑灾害基本特征与成因机理初步研究[J].工程地质学报,2009,17(4):433-444.
[2] 谢洪,王成华,林立相.标水岩沟滑坡型泥石流灾害及特征[J].中国地质灾害与防治学报,2000,11(3):23-25,30.
[3] 季宪军,欧国强,杨顺,等.崩滑土体坡面运动过程研究现状与展望[J].山地学报,2012,30(3):361-368.
[4] 胡厚田,刘涌江,邢爱国.高速远程滑坡流体动力学理论的研究[M].成都:西南交通大学出版社,2003.
[5] 刘涌江.大型高速岩质滑坡流体化理论研究[D].成都:西南交通大学,2002.
[6] Savage S B, Hutter K. The dynamics of avalanches of granular materials from initiation to runout(Part I): Analysis[J]. Acta Mechanica, 1991,86(1/2/3/4):201-223.
[7] Pastor M, Merodo J A F, Herreros M I, et al. Mathematical, constitutive and numerical modelling of catastrophic landslides and related phenomena[J]. Rock Mechanics and Rock Engineering, 2008,41(1):85-132.
[8] 王涛,盛谦,熊将.基于颗粒流方法自然崩落法数值模拟研究[J].岩石力学与工程学报,2007,26(S2):4202-4207.
[9] 郑智能,张永兴,董强,等.边坡落石灾害的颗粒流模拟方法[J].中国地质灾害与防治学报,2008,19(3):46-49.
[10] 梁鑫,郑立宁.土石碎屑体稳定性离散元数值分析[J].铁道建筑, 2011(2):91-93.
[11] 左自波,张璐璐,王建华.降雨触发不同级配堆积体滑坡模型试验研究[J].岩土工程学报,2015,37(7):1319-1327.
[12] 周中,傅鹤林,刘宝琛,等.土石混合体边坡人工降雨模拟试验研究[J].岩土力学,2007,28(7):1391-1396.
[13] 刘波,罗先启,张振华.三峡库区千将坪滑坡模型试验研究[J].三峡大学学报:自然科学版,2007,29(2):124-128.
[14] 吴火珍,冯美果,焦玉勇,等.降雨条件下堆积层滑坡体滑动机制分析[J].岩土力学,2010,31(S1):324-329.
[15] 李焕强,孙红月,孙新民,等.降雨入渗对边坡性状影响的模型试验研究[J].岩土工程学报,2009,31(4):589-594.
[16] 尹洪江,王志兵,胡明鉴.降雨强度对松散堆积土斜坡破坏的模型试验研究[J].土工基础,2011,25(3):74-76.
Influence of Mud on Migration Process of Viscous Debris Flow
JI Xianjun1, LIANG Ying1, PAN Huali2, OU Guoqiang2
(1.NanyanInstituteofTechnology,Nanyang,He’nan473004,China; 2.InstituteofMountainHazardsandEnvironment,ChineseAcademyofSciences,Chengdu,Sichuan610041,China)
[Objective] The aim of the study is to analyze the influence of mud on the moving ways, width and longitudinal distance and velocity of viscous debris flow on slope, and help to provide the references for disaster prevention. [Methods] The experimental model was built for viscous debris flow, and a series of model experiments were carried out through the device. The viscous debris flow composed of Chengdu clay mud and coarse particles. [Results] The adhesion force between the coarse particles increased, and the movement patterns changed from the inviscid debris flow to the viscous debris flow, and to the massive sliding with increasing mud density. The width and distance on slope decreased with increasing mud density. The migration process could be differentiated according to mud density. The velocity increases rapidly and the gradient is large when mud density was lower than 1.413 g/cm3. The migration process can be divided into two stages when mud density was higher than 1.413 g/cm3, the velocity increased slowly and the gradient changes little in the first stage but the velocity increased quickly, and the gradient changed quickly in the second stage. [Conclusion] The mud affects the movement pattern and the moving process of viscous debris flow.
viscous debris flow; movement pattern; model experiment; mud
2016-05-28
2016-06-17
国家自然科学基金面上项目“黏性碎屑流坡面运移动力过程研究”(41672357); 国家自然科学资助项目(41372331); 国家国际科技合作专项项目(2013DFA21720); 河南省科技公关项目(162102310253); 河南省高等学校重点科研项目(15A410005)
季宪军(1974—),男(汉族),河南省信阳人,博士,副教授,主要从事岩土工程的教学与理论研究。E-mail:jifeng988@163.com。
欧国强(1958—),男(汉族),四川省成都市人,研究员,博士生导师,主要从事泥石流与泥沙研究。E-mail:ougq@imde.ac.cn。
A
1000-288X(2017)01-0088-05
TU411, P642.2

