基于非对称属性的SVD推荐算法的研究

黄浩

摘要：该文在传统的基于奇异值矩阵分解模型（SVD）的基础上提出一种非对称的协同过滤算法，对电影的评分进行预测。并在Movielens数据集上实验验证，该算法在平均误差方根（RMSE）上比SVD、SVD++的算法更优。

关键词：电影评分预测；SVD；RMSE；矩阵分解

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2017）03-0079-02

1 研究背景

推荐系统现已广泛应用于很多领域，其中最典型并具有良好的发展和应用前景的领域就是电子商务领域，比如亚马逊（Amazon）、谷歌新闻（Google News）以及国内的淘宝网等知名互联网巨头。一般来说，个性化推荐是根据用户的特点或购买行为，向用户推荐其感兴趣的信息。但同时，随着电子商务规模的不断扩大，商品个数和种类快速增长，用户需要花费大量的时间才能找到自己想买的商品。这种浏览大量无关的信息和产品过程无疑会使淹没在信息过载问题中的消费者不断流失。为了解决所谓的“信息过载”问题，针对特定每一个用户的个性化推荐系统应景而生。特别是近几年来，随着学术界对推荐系统的研究热度不断攀升，已经形成了一门相对独立的学科。

1.1 基于电影评分预测的推荐算法

当今社会，人们把欣赏电影当成日常娱乐中一种不可或缺的方式。有很多电影的评分网站允许用户根据其喜好程度对电影进行评分，比如IMDB，豆瓣以及一些提供在線观看的网站。然而，对于某个用户而言，并不是所有的电影都观看并且评分了。对这些缺失的评分有很多算法对其进行预测，其中典型的有基于内容的评分预测和协同过滤算法。

2 实验数据集和评价指标

2.1 Movielens数据集

实验使用Grouplens网站开放给用户的电影评分数据集，其中Movielens 100K数据集包含943个用户对1682部电影的10万条评分记录（评分范围1-5分，每个用户至少对20部电影进行了评分），此数据集的稀疏度为93.7%。本文采用其中ua.base和ua.test作为训练集和测试集，即80%的数据作为训练集，余下的20%的数据作为测试集，并以此对本文提出的推荐算法进行实验。

2.2 评价指标

实际上，针对推荐算法性能优劣的衡量方法有很多，如平均绝对误差（MAE）、平均方根偏差（RMSE）、覆盖率（COV）等。本文主要采用RMSE值作为算法优劣的评价标准，即通过计算预测值与真实值的平均绝对误差来判断推荐算法的好坏，推荐精度的高低与RMSE值的大小成反比。其公式如下：

[RMSE=1Stest（u，i）∈Stest（rui-rui）2]

其中，Stest为测试集中有评分记录的集合内元素的计数， [rui]为用户u对电影i的预测评分，[rui]为测试集中用户u对电影i的真实评分。

3 算法

3.1 基线预测算法

多数情况下，人们早已发现用户对电影的评分往往具有很多与电影无关的因素，用户有一些属性和电影无关，电影也有一些属性和用户无关。因此，一种将偏置项加入到推荐算法当中，并将其称为基线预测算法。定义对一部电影评分的预测值为[rui]，那么其公式为：

[rui=μ+bi+bu]

其中，[μ]表示所有评分的平均值；[bi]表示电影的偏移量，代表电影在接受评分时与用户无关的因素；[bu]表示用户的偏移量，代表用户在评分中与电影无关的因素。

3.2 SVD算法

但基线预测无法针对用户的潜在偏好进行评分预测，因人们对电影进行评分的时候极可能有一些偏好，如A用户对科幻片比较感兴趣，那么该用户在对其他具有科幻特征的电影评分很可能偏高，而对非科幻片的潜在评分就很可能偏低。因此我们引入2个特征向量：[pu]和[qi]。其中[pu]表示用户对不同风格的电影的偏好，[qi]表示不同风格的用户对电影的偏好。那么，在基线预测的基础上加入上述向量，对电影评分的预测值公式为：

[rui=μ+bi+bu+qTipu]

为了得到更为准确的特征向量值，通常采用随机梯度下降法来训练上述各参量，以防止过拟合。其更新公式分别为：

[bu←bu+α1?（eui-β1?bu）]

[bi←bi+α1?（eui-β1?bi）]

[qi←qi+α2?（euipu-β2?qi）]

[pu←pu+α2?（euiqi-β2?pu）]

其中，定义[eui]为每次迭代训练中用户u对电影i的预测评分与真实评分之差。

3.3 SVD++算法

在SVD算法的基础上，Keron等人提出把隐式反馈信息融入到SVD算法中，形成了SVD++算法。算法使用R（u）表示被用户评分的电影的集合， [yj]为隐主题的维度向量，其向量值与[pu]、[qi]的向量值一致，表示隐式反馈信息的聚类。那么，对用户偏好建模的同时加入了用户已评分电影的反馈来修正用户在隐主题上的偏好。当然，此处的隐性反馈并没有直观地反映出来用户对该电影的喜欢或厌恶程度， 而是仅仅表明该用户隐性地对该电影进行了评分，表明用户隐性的反馈不是随机的，而是有一定目的的。使用该信息就能够很大程度上提升系统的效果。那么，其对电影评分的预测值公式为：

[rui=μ+bi+bu+qTi（pu+R（u）-12j∈R（u）yj）]

其他参量的更新式保持不变，[yj]的更新式如下：

[yj←yj+α2?（eui?R（u）-12?qi-β2?qi）]

3.4 非对称SVD算法

最后本文提出把用户已看过或已浏览过（但未评分）的电影作为反馈信息融入到SVD++算法中，用[xj]表示。其对电影评分的预测值公式为：

[rui=μ+bi+bu+qTi?R（u）-12?j∈R（u）（ruj-buj）xj+yj]

[xj]的更新式为：

[xj←xj+α2?i，j∈R（u）eui?R（u）-12?qi（ruj-μ-buj）-β2?xj]

在公式中无[pu]参量，因此[pu]不用更新，其它参量的更新式保持不变。

4 实验结果和分析

4.1 实验结果

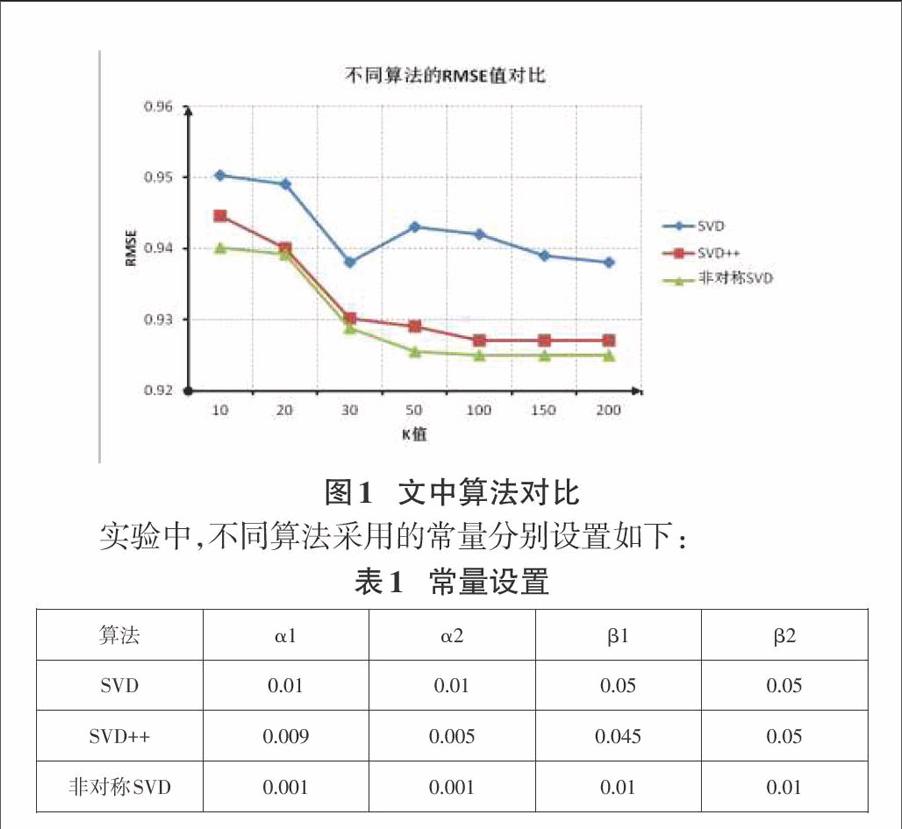
在Movielens数据集上进行实验，我们选取不同的向量维度（用K表示），测试SVD、SVD++和非对称SVD算法的RMSE值。结果如图1所示。

实验中，不同算法采用的常量分别设置如下：

[算法＼&α1＼&α2＼&β1＼&β2＼&SVD＼&0.01＼&0.01＼&0.05＼&0.05＼&SVD++＼&0.009＼&0.005＼&0.045＼&0.05＼&非对称SVD＼&0.001＼&0.001＼&0.01＼&0.01＼&]

5 结束语

对本文提出的几种算法，我们在Movielens数据集上进行实验，证明在RMSE值的对比上，非对称SVD算法比其他本文提到的算法更为优秀。能够得到比传统SVD模型更好的评分预测结果和推荐结果。另一方面，非对称SVD 算法继承了SVD 算法的优点，能够较好地解决用户-电影矩阵稀疏性的问题，在用户共同评分较少的情况下也能得到较好的实验结果。当然，当今互联网上社交型网络也越来越受到用户关注和使用，今后考虑把用户之间的社交关系和项目元数据也融入算法当中，使之能更有效地进行评分预测。

参考文献：

[1] Wu J L. Collaborative filtering on the Netflix prize database[EB/OL]. http：//dsec.pku.edu.cn/～jinlong/.

[2] 李改， 李磊. 基于矩阵分解的协同过滤算法[J]. 计算机工程与应用， 2011， 47（30）： 4-7.

[3] 徐翔， 王煦法. 基于SVD的协同过滤算法的欺诈攻击行为分析[J]. 计算机工程与应用， 2009， 45（20）： 92-95.

[4] 冯婧姣. 个性化推荐协同过滤算法研究[D]. 哈尔滨： 哈尔滨工程大学， 2015.

[5] 张光卫， 李德毅， 李鹏. 基于云模型的协同过滤推荐算法[J]. 软件学报， 2007， 18（10）： 2403-2411.