基于KMP算法的next数组
陈子轩

摘要:該文主要叙述了基于KMP算法的next数组的理解,分析了在C++环境中利用next数组对KMP算法的具体实现,使该算法更加方便实用。
关键词:KMP算法;next数组;匹配
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2017)03-0066-01
1 概述
字符串匹配是现代科学中的基本问题,如文献目录检索系统与生物基因序列匹配工程。对于这一问题的研究,D.E.Knuth,J.H.Morris和V.R.Pratt改进了Brute-Force算法,提出一种线性时间复杂的字符串匹配算法——KMP算法,该算法利用了上一次匹配失败的反馈信息,通过模式串对应的next数组减少回溯,成功地将时间复杂度由O(m*n)降低至O(m+n),从而达到快速匹配。
2 next数组的定义
next数组作为KMP算法中的关键,其特点是模式串每一位对应的next值仅依赖模式串本身,而与主串无关。普遍定义[1]如下:
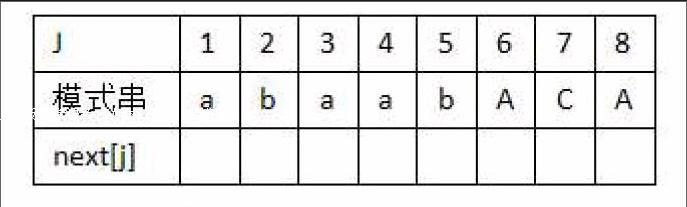
[next[j]=-1 j=0max{k|1≤k 其中模式串T(T0T1…Tm,m≥0)中每一个Tj (0≤j≤m)对应的next值以next[j]表示。 3 next数组的理解 1)由next数组的定义可知,每个模式串都有对应的唯一确定的next数组。对next数组可从两个方面来理解:next数组是用来记录字符串匹配过程中匹配失败情况下可以向前多跳几个字符(模式串本身局部匹配的信息);next数组是用来描述模式串的对称程度的,数组的值越大,对称程度越高。 2) next数组的实现采用了递推思想,即以赋值定义next[0]=0为起点,通过next[0]算出next[1]的值,进而得到next[2]、next[3]、……、next[i]的值。 假设已求得next[j]=k,根据定义可得”T0T1…Tk-1”=” Tj-kTj-k+1 …Tj-1”,那么求next[j+1]的值可以分为以下两种情况: 1°若Tk= Tj,则”T0T1…Tk”=” Tj-kTj-k+1 …Tj”,并且不可能存在k>k满足上式,那么next[j+1]=k+1,即next[j+1]=next[j]+1。 2°若Tk!= Tj,则”T0T1…Tk”!=” Tj-kTj-k+1 …Tj”。设k=k1时,满足Tk1=Tj,下求k1。 图1 图2 由图1可知实际上就是将模式串T往右移,移动后T的j对应T的k1。 考虑另一个前提条件:”T0T1…Tk1-1”=” Tj-k1Tj-k1+1 …Tj-1”。实际上k1=next[k],但满足了上述条件不一定就满足Tk1=Tj。也就是说仅移动一次不一定满足Tk1=Tj。如果移动一次后得到k1仍然不满足Tk1=Tj,就要按照前提条件再移动一次。 由图2,依此类推,直到Tkn=Tj或kn=0为止。此时有next[j+1]= kn+1,而kn=next[kn-1]且k1=k=next[j],由于kn 4 有关next数组的题目解法 例.在KMP模式匹配算法中,需要求解串中P的next函数值,其定义如下(其中j为模式中符号的序号)。对于模式串”abaabaca”,其next函数值序列为多少。 [next[j]=0 j=1max{k|1 解 首先把字符串填入到一个表格中, 将j导入next函数,即可求解。 如j=1时,next[1]=0; j=2时,1 (上接第66页) 即”ab”=”ba”,不成立,舍去。再取k=2(T1=T3),即”a”=”a”,成立。于是max{k}=2,即next[4]=2; 同理可得next数组中其他元素的值。 所以结果为: 5 next数组在C++环境下的实现 通过递推思想得到的计算next数组算法用C++语言描述如下: void makeNext(const char P[],int next[]) {int q,k,m=strlen(P); next[0]=0; for(q=1,k=0;q {while(k>0&&P[q]!=P[k]) k=next[k-1]; if(P[q]==P[k]) k++; next[q]=k; }} 6 总结 本文重点解释了next数组的原理。next数组在模式串与主串匹配失败时可索引模式串向前滑动的距离数,在KMP算法中至关重要,并给出C++语言下next数组的代码,以具体实现。 参考文献: [1] 王红梅, 胡明, 王涛.数据结构(C++版)[M].北京:清华大学出版社,2011. [2] 汤亚玲. KMP算法中next数组的计算方法研究[J]. 计算机技术与发展, 2009, 19(6):98-101. [3] 杨薇薇, 廖翔. 一种改进的BM模式匹配算法[J]. 计算机应用, 2006, 26(2):318-319.

